Powerpoint 3.3
... Example 2B: Determining Whether Lines are Parallel Use the given information and the theorems you have learned to show that r || s. m2 = (10x + 8)°, m3 = (25x – 3)°, x = 5 ...
... Example 2B: Determining Whether Lines are Parallel Use the given information and the theorems you have learned to show that r || s. m2 = (10x + 8)°, m3 = (25x – 3)°, x = 5 ...
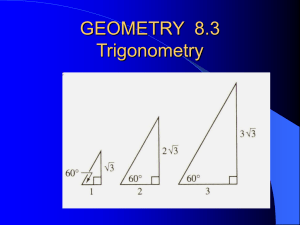
GEOMETRY 8.3 Trigonometry
... He can Calculate ALL three (Equations) Thank you SOHCAHTOA I’m Really Glad to Know Ya You’re the CHIEF of Trigonometry ...
... He can Calculate ALL three (Equations) Thank you SOHCAHTOA I’m Really Glad to Know Ya You’re the CHIEF of Trigonometry ...
Unit 1 Review
... h. segment ____ 18. a point at an end of a segment or the starting point of a ray ____ 19. a part of a line that starts at an endpoint and extends forever in one direction ____ 20. a statement that is accepted as true without proof, also called an axiom ____ 21. the common endpoint of the sides of a ...
... h. segment ____ 18. a point at an end of a segment or the starting point of a ray ____ 19. a part of a line that starts at an endpoint and extends forever in one direction ____ 20. a statement that is accepted as true without proof, also called an axiom ____ 21. the common endpoint of the sides of a ...
Geometry - Chapter 1 Day #1 - Somerset Independent Schools
... What is the converse of the following statement? "If a whole number has a as its last digit, then the number is evenly divisible by 10./1 a. If a number is evenly divisible by la, then it is a whole number. b. If a whole number is divisible by la, then it is an even number. c. If a whole number is e ...
... What is the converse of the following statement? "If a whole number has a as its last digit, then the number is evenly divisible by 10./1 a. If a number is evenly divisible by la, then it is a whole number. b. If a whole number is divisible by la, then it is an even number. c. If a whole number is e ...
Geometry_Units_of_Study - Asbury Park School District
... segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. G.SRT.5 Prove theorems involving similarity. Use congruenc ...
... segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. G.SRT.5 Prove theorems involving similarity. Use congruenc ...
GeometryPowerStandards Student Copy
... ● LT3: Construct a viable argument to justify a solution method. ● LT4: Identify pairs of angles as complementary, supplementary, adjacent, or vertical, and apply these relationships to determine missing angle measures ● LT5: Prove triangles congruent using SSS, SAS, ASA, AAS, and HL. Prove parts of ...
... ● LT3: Construct a viable argument to justify a solution method. ● LT4: Identify pairs of angles as complementary, supplementary, adjacent, or vertical, and apply these relationships to determine missing angle measures ● LT5: Prove triangles congruent using SSS, SAS, ASA, AAS, and HL. Prove parts of ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.