Geometry IV
... 4. Do not waste any time. If you cannot answer a question, go on to the next one immediately. 5. When you have answered as many questions as you can, correct your answers using the answer key which follows the diagnostic test. 6. To be considered correct, answers must be identical to those in the ke ...
... 4. Do not waste any time. If you cannot answer a question, go on to the next one immediately. 5. When you have answered as many questions as you can, correct your answers using the answer key which follows the diagnostic test. 6. To be considered correct, answers must be identical to those in the ke ...
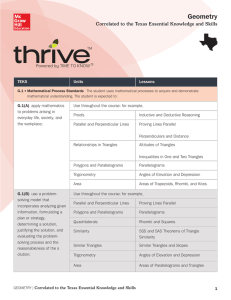
Geometry Correlated to TEKS
... G.12(D) describe radian measure of an angle as the ratio of the length of an arc intercepted by a central angle and the radius of the circle; and ...
... G.12(D) describe radian measure of an angle as the ratio of the length of an arc intercepted by a central angle and the radius of the circle; and ...
Minimal surfaces from circle patterns: Geometry from
... circle packings [14]. It is an interesting question whether the convergence of discrete minimal surfaces is as good. Because of the convergence, the theory developed in this paper may be used to obtain new results in the theory of smooth minimal surfaces. A typical problem in the theory of minimal s ...
... circle packings [14]. It is an interesting question whether the convergence of discrete minimal surfaces is as good. Because of the convergence, the theory developed in this paper may be used to obtain new results in the theory of smooth minimal surfaces. A typical problem in the theory of minimal s ...
Geometry - Kingdom Schools
... Find the lengths of segments formed by lines that intersect circles and use the lengths to solve related problems. • write the equation of a circle in the coordinate plane. Use the equation of a circle to graph the circle and solve related problems. ...
... Find the lengths of segments formed by lines that intersect circles and use the lengths to solve related problems. • write the equation of a circle in the coordinate plane. Use the equation of a circle to graph the circle and solve related problems. ...
conjecture. - Nutley Public Schools
... Using Inductive Reasoning to 2-1 Make Conjectures Determine if each conjecture is true or false based on the information. If false, give a counter-example. 1.Given: AB, BC and CD Conjecture: A, B, C and D are collinear. ...
... Using Inductive Reasoning to 2-1 Make Conjectures Determine if each conjecture is true or false based on the information. If false, give a counter-example. 1.Given: AB, BC and CD Conjecture: A, B, C and D are collinear. ...
Geometry Honors - Spring Grove Area School District
... Identify and solve angle pairs formed by two intersecting lines Identify and solve angle pairs formed by three intersecting lines. Identify and solve angle pairs formed by parallel lines and a transversal Use angle relationships to prove lines are parallel Write paragraph proofs using geom ...
... Identify and solve angle pairs formed by two intersecting lines Identify and solve angle pairs formed by three intersecting lines. Identify and solve angle pairs formed by parallel lines and a transversal Use angle relationships to prove lines are parallel Write paragraph proofs using geom ...
NUMBER STRAND – Geometry - TEAM-Math
... Version,” is intended for teachers who have completed the TEAM-Math Summer Institute and have been introduced to the Interactive Mathematics Program. An alternative version is intended for those who have not yet attended the Summer Institute. The Appendix provides the correlation of objectives, whic ...
... Version,” is intended for teachers who have completed the TEAM-Math Summer Institute and have been introduced to the Interactive Mathematics Program. An alternative version is intended for those who have not yet attended the Summer Institute. The Appendix provides the correlation of objectives, whic ...
Circles
... not a right triangle and thus the radius is not perpendicular to the line m, therefore the line is not tangent to the circle. ...
... not a right triangle and thus the radius is not perpendicular to the line m, therefore the line is not tangent to the circle. ...
Geometry Pacing Guide Last Updated: August, 2015 Days Unit
... and to prove relationships in geometric figures. ♦ G-GPE.4: Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1,√3) lies on the circle c ...
... and to prove relationships in geometric figures. ♦ G-GPE.4: Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1,√3) lies on the circle c ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.