circles - Tikhor
... 5) If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord. 6) Given an arc of a circle, complete the circle. 7) If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prov ...
... 5) If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord. 6) Given an arc of a circle, complete the circle. 7) If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prov ...
Geometry Honors - Belvidere School District
... Unit Summary: Identify points, lines, planes, angles, and their relationships. Measure segments, angles, and polygons using a variety of methods. Introduce the terms and symbols of geometry. Make conjectures about vertical angles, linear pairs of angles, midpoints, and distance. Explore these proper ...
... Unit Summary: Identify points, lines, planes, angles, and their relationships. Measure segments, angles, and polygons using a variety of methods. Introduce the terms and symbols of geometry. Make conjectures about vertical angles, linear pairs of angles, midpoints, and distance. Explore these proper ...
Geometry - Pearson
... This document demonstrates how Pearson’s High School Series by Elayn Martin-Gay, ©2016, meets the standards of the Common Core State Standards for Mathematics, PARRC Model Content Frameworks Mathematics - Algebra I. Pearson’s High School Series by Elayn Martin-Gay, ©2016, consists of three fully-dig ...
... This document demonstrates how Pearson’s High School Series by Elayn Martin-Gay, ©2016, meets the standards of the Common Core State Standards for Mathematics, PARRC Model Content Frameworks Mathematics - Algebra I. Pearson’s High School Series by Elayn Martin-Gay, ©2016, consists of three fully-dig ...
File
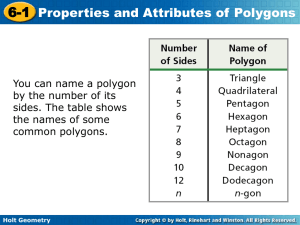
... All the sides are congruent in an equilateral polygon. All the angles are congruent in an equiangular polygon. A regular polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. ...
... All the sides are congruent in an equilateral polygon. All the angles are congruent in an equiangular polygon. A regular polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. ...
Geom-vocab-I-can - Hale County School
... 45. Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. [S-CP5] Example: Compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer. 46. Find the conditional probabili ...
... 45. Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. [S-CP5] Example: Compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer. 46. Find the conditional probabili ...
Slides for Nov. 12, 2014, lecture
... imposes additional structure; unboundedness is an extension relation, because it is qualitative and not quantitative, as opposed to infinitude, which is a measure relation because it is quantitative; (for cognoscenti: the extension relations are the differential structure and topology of a manifold) ...
... imposes additional structure; unboundedness is an extension relation, because it is qualitative and not quantitative, as opposed to infinitude, which is a measure relation because it is quantitative; (for cognoscenti: the extension relations are the differential structure and topology of a manifold) ...
Ā - Non-Aristotelian Evaluating
... "Thales was the first to go into Egypt and bring back this learning (geometry) into Greece. He discovered many propositions himself, and he disclosed to his successors the underlying principles of many others, in some cases his methods being more general in others more empirical". Proclus further cr ...
... "Thales was the first to go into Egypt and bring back this learning (geometry) into Greece. He discovered many propositions himself, and he disclosed to his successors the underlying principles of many others, in some cases his methods being more general in others more empirical". Proclus further cr ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.