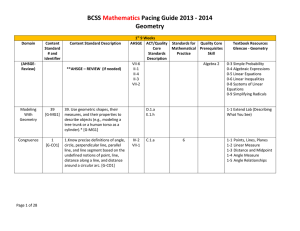
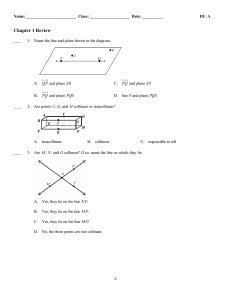
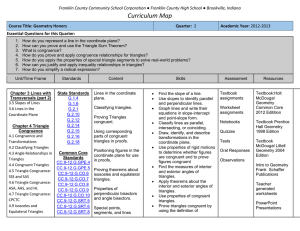
Chapter 1 - South Henry School Corporation
... 1. Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in t ...
... 1. Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in t ...
File
... B. COORDINATE GEOMETRY The vertices of ΔRST are R(–3, 0), S(0, 5), and T(1, 1). The vertices of ΔRST are R(3, 0), S(0, –5), and T(–1, –1). Use the Distance Formula to verify that corresponding sides are congruent. Name the congruence transformation for ΔRST and ΔRST. ...
... B. COORDINATE GEOMETRY The vertices of ΔRST are R(–3, 0), S(0, 5), and T(1, 1). The vertices of ΔRST are R(3, 0), S(0, –5), and T(–1, –1). Use the Distance Formula to verify that corresponding sides are congruent. Name the congruence transformation for ΔRST and ΔRST. ...
09 15 Weekly Lesson Plans
... a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. MCC9-12.G.SRT.2 Given two figures, use the definition o ...
... a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. MCC9-12.G.SRT.2 Given two figures, use the definition o ...
Here - University of New Brunswick
... Just what is ‘substantial’ is a matter of judgement. There is no avoiding this - only with some experience will you be able to judge what can be assumed and what cannot. ...
... Just what is ‘substantial’ is a matter of judgement. There is no avoiding this - only with some experience will you be able to judge what can be assumed and what cannot. ...
similar polygons
... Ratios in Similar Polygons A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons. The similarity ratio of ∆ABC to ∆DEF is __2:1_____. The similarity ratio of ∆DEF to ∆ABC is __1:2_____. ...
... Ratios in Similar Polygons A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons. The similarity ratio of ∆ABC to ∆DEF is __2:1_____. The similarity ratio of ∆DEF to ∆ABC is __1:2_____. ...
Sunrise on the First Day of a New Year Learning Task
... The material for unit 3 starts with a representation of the fundamental figures used in the study of lines, line segments, angles, and their relationships to the circle(s) they intersect. The tasks are focused on investigating properties and relationships that occur among circles, lines, and angles ...
... The material for unit 3 starts with a representation of the fundamental figures used in the study of lines, line segments, angles, and their relationships to the circle(s) they intersect. The tasks are focused on investigating properties and relationships that occur among circles, lines, and angles ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.