Chapter 2 - UT Mathematics
... textbooks - in Coxeter’s book “Introduction to Geometry”, for instance, - or in many college textbooks where the focus is on developing geometry within an axiomatic system. Because nothing is assumed about the existence or multiplicity of parallel lines, however, Absolute Geometry is not very intere ...
... textbooks - in Coxeter’s book “Introduction to Geometry”, for instance, - or in many college textbooks where the focus is on developing geometry within an axiomatic system. Because nothing is assumed about the existence or multiplicity of parallel lines, however, Absolute Geometry is not very intere ...
SMSG Geometry Summary
... 2. Postulate 9. (The Plane Separation Postulate.) Given a line and a plane containing it. The points of the plane that do not lie on the line form two sets such that (1) each of the sets is convex and (2) if P is in one set and Q is in the other then the segment P Q intersects the line. 3. Definitio ...
... 2. Postulate 9. (The Plane Separation Postulate.) Given a line and a plane containing it. The points of the plane that do not lie on the line form two sets such that (1) each of the sets is convex and (2) if P is in one set and Q is in the other then the segment P Q intersects the line. 3. Definitio ...
SMSG Geometry Summary
... 2. Postulate 9. (The Plane Separation Postulate.) Given a line and a plane containing it. The points of the plane that do not lie on the line form two sets such that (1) each of the sets is convex and (2) if P is in one set and Q is in the other then the segment P Q intersects the line. 3. Definitio ...
... 2. Postulate 9. (The Plane Separation Postulate.) Given a line and a plane containing it. The points of the plane that do not lie on the line form two sets such that (1) each of the sets is convex and (2) if P is in one set and Q is in the other then the segment P Q intersects the line. 3. Definitio ...
Project Gutenberg`s The Foundations of Geometry, by David Hilbert
... The material contained in the following translation was given in substance by Professor Hilbert as a course of lectures on euclidean geometry at the University of Göttingen during the winter semester of 1898–1899. The results of his investigation were re-arranged and put into the form in which they ...
... The material contained in the following translation was given in substance by Professor Hilbert as a course of lectures on euclidean geometry at the University of Göttingen during the winter semester of 1898–1899. The results of his investigation were re-arranged and put into the form in which they ...
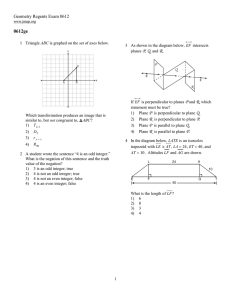
2-1
... Check It Out! Example 3 Make a conjecture about the lengths of male and female whales based on the data. Average Whale Lengths Length of Female (ft) ...
... Check It Out! Example 3 Make a conjecture about the lengths of male and female whales based on the data. Average Whale Lengths Length of Female (ft) ...
8-1 Similar polygons
... Ratios in Similar Polygons Check It Out! Example 3 A boxcar has the dimensions shown. A model of the boxcar is 1.25 in. wide. Find the length of the model to the nearest inch. ...
... Ratios in Similar Polygons Check It Out! Example 3 A boxcar has the dimensions shown. A model of the boxcar is 1.25 in. wide. Find the length of the model to the nearest inch. ...
Andrew Maneggia Superintendent Honors Geometry Curriculum
... of the fundamental concepts of Euclidean Geometry. Algebra skills developed in the previous course will be integrated throughout the curriculum. The inductive as well as the deductive thought processes will be employed with strong emphasis on logical sequential reasoning. ...
... of the fundamental concepts of Euclidean Geometry. Algebra skills developed in the previous course will be integrated throughout the curriculum. The inductive as well as the deductive thought processes will be employed with strong emphasis on logical sequential reasoning. ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.