Geometer`s Sketchpad and the New Geometry Strands
... Do any of the four centers always remain inside the circle? If a center is moved outside of the triangle, under what circumstances will it happen? Are the four centers ever collinear? If so, under what circumstances? Describe what happens to the centers if the triangle is a right triangle. ...
... Do any of the four centers always remain inside the circle? If a center is moved outside of the triangle, under what circumstances will it happen? Are the four centers ever collinear? If so, under what circumstances? Describe what happens to the centers if the triangle is a right triangle. ...
Algebra I Detailed Objectives
... 3. Use properties of parallel lines and proportional reasoning to find lengths of segments. 1. Use trigonometric ratios to find the measures of sides of right triangles to solve problems. 2. Use trigonometric ratios to find the measures of angles in right triangles to solve problems. 3. Use trigonom ...
... 3. Use properties of parallel lines and proportional reasoning to find lengths of segments. 1. Use trigonometric ratios to find the measures of sides of right triangles to solve problems. 2. Use trigonometric ratios to find the measures of angles in right triangles to solve problems. 3. Use trigonom ...
3 - Project Maths
... gain insights into students’ algebraic reasoning in second year. It is envisaged that this competency test be administered to second- year students at the beginning of the year. Analysis of the outcomes of the test will inform planning for interventions and measures to be taken to address any proble ...
... gain insights into students’ algebraic reasoning in second year. It is envisaged that this competency test be administered to second- year students at the beginning of the year. Analysis of the outcomes of the test will inform planning for interventions and measures to be taken to address any proble ...
History and Philosophy of Mathematics MA0010
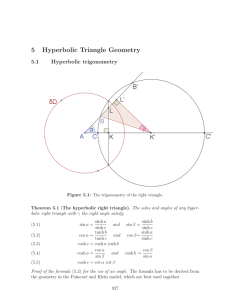
... 1. In Euclidean geometry the lines remain at a constant distance from each other, and are known as parallels. 2. In hyperbolic geometry they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often ...
... 1. In Euclidean geometry the lines remain at a constant distance from each other, and are known as parallels. 2. In hyperbolic geometry they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often ...
Georgia Milestones Study Guide for TCSS Unit
... circle, area of a circle, volume of a cylinder, pyramid, and cone. Use dissection arguments, Cavalieri’s principle, and informal limit arguments. MCC9-12.G.GMD.3 Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.★ ...
... circle, area of a circle, volume of a cylinder, pyramid, and cone. Use dissection arguments, Cavalieri’s principle, and informal limit arguments. MCC9-12.G.GMD.3 Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.★ ...
Foundations of Geometry
... All of the points of a which lie upon the same side of O, when taken together, are called the half-ray emanating from O. Hence, each point of a straight line divides it into two half-rays. Making use of the notation of theorem 5, we say: The points A, A0 lie in the plane α upon one and the same side ...
... All of the points of a which lie upon the same side of O, when taken together, are called the half-ray emanating from O. Hence, each point of a straight line divides it into two half-rays. Making use of the notation of theorem 5, we say: The points A, A0 lie in the plane α upon one and the same side ...
2-1 2-1 Using Inductive Reasoning to Make Conjectures
... 2-1 Make Conjectures When several examples form a pattern and you assume the pattern will continue, you are applying inductive reasoning. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true. You may use inductive reasoning to draw a conclu ...
... 2-1 Make Conjectures When several examples form a pattern and you assume the pattern will continue, you are applying inductive reasoning. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true. You may use inductive reasoning to draw a conclu ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.