3.3 PPT - Nutley Schools
... Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. (aka plug in the value of x and see if it gives you a true statement.) m3 = (4x – 80)°, m7 = (3x – 50)°, x = 30 ...
... Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. (aka plug in the value of x and see if it gives you a true statement.) m3 = (4x – 80)°, m7 = (3x – 50)°, x = 30 ...
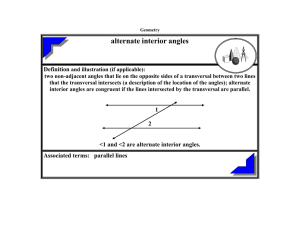
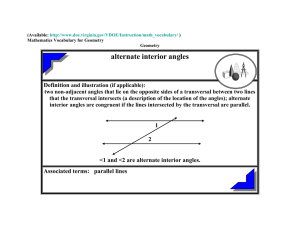
alternate interior angles
... dimension one, a plane dimension two, and space dimension three. The points of n-dimensional space have n coordinates ( x1, x2 , …, xn ). ...
... dimension one, a plane dimension two, and space dimension three. The points of n-dimensional space have n coordinates ( x1, x2 , …, xn ). ...
Geometry Vocabulary
... dimension one, a plane dimension two, and space dimension three. The points of n-dimensional space have n coordinates ( x1, x2 , …, xn ). ...
... dimension one, a plane dimension two, and space dimension three. The points of n-dimensional space have n coordinates ( x1, x2 , …, xn ). ...
Geometry 21 - Fairfield Public Schools
... an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects. For example, they can see 5 – 3(x – y)2 as 5 minus a positive number times a square and use that to realize that its value cannot be more ...
... an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects. For example, they can see 5 – 3(x – y)2 as 5 minus a positive number times a square and use that to realize that its value cannot be more ...
Unit 1 – Transformations Terms and Definitions
... glossary to be developed during the module. Terms, definitions, and conjectures which arise during the module can be added to the glossary. The activity, which should take no longer than 30 minutes, can be divided up so that each group defines a different set of terms. The terms have been grouped fo ...
... glossary to be developed during the module. Terms, definitions, and conjectures which arise during the module can be added to the glossary. The activity, which should take no longer than 30 minutes, can be divided up so that each group defines a different set of terms. The terms have been grouped fo ...
PACING_GUIDE_GEOMETRY_
... How can a two dimensional figure be folded into a three dimensional solid? To what extent does the area of a two dimensional figure relate to the surface area and volume of a three dimensional figure? How can ratios be applied to similar solids to determine surface area and volume? ...
... How can a two dimensional figure be folded into a three dimensional solid? To what extent does the area of a two dimensional figure relate to the surface area and volume of a three dimensional figure? How can ratios be applied to similar solids to determine surface area and volume? ...
1/1 - Math K-12
... There is exactly one line through any two points. There is exactly one plane through any three noncollinear points. ...
... There is exactly one line through any two points. There is exactly one plane through any three noncollinear points. ...
Course Notes - Mathematics
... which are numbered for the reader’s convenience; the numbers are not part of the message.” To get you started, the first paragraph is merely a transmission of the 24 symbols to be used in the rest of the message. 1. A. B. C. D. E. F. G. H. I. J. K. L. M. N. P. Q. R. S. T. U. V. W. Y. Z. 2. A A, B; A ...
... which are numbered for the reader’s convenience; the numbers are not part of the message.” To get you started, the first paragraph is merely a transmission of the 24 symbols to be used in the rest of the message. 1. A. B. C. D. E. F. G. H. I. J. K. L. M. N. P. Q. R. S. T. U. V. W. Y. Z. 2. A A, B; A ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.