Download 3.3 PPT - Nutley Schools

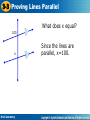
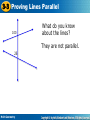
3-3
3-3 Proving
ProvingLines
LinesParallel
Parallel
Warm Up
Lesson Presentation
Lesson Quiz
Holt
Geometry
Holt
Geometry
3-3 Proving Lines Parallel
Warm up intro: The converse of a theorem
is found by exchanging the hypothesis
(beginning of the sentence) and the
conclusion (end of the sentence.
The converse of a theorem is not
automatically true.
For example: If the sun is shining, I
can see my shadow outside.
The converse: If I can see my shadow
outside, the sun is shining.
Holt Geometry
3-3 Proving Lines Parallel
Warm Up
State the converse of each statement.
1. If a = b, then a + c = b + c.
If a + c = b + c, then a = b.
2. If mA + mB =
complementary.
If A and  B are
then mA + mB
3. If AB + BC = AC,
90°, then A and B are
complementary,
=90°.
then A, B, and C are collinear.
If A, B, and C are collinear, then AB + BC = AC.
Holt Geometry
3-3 Proving Lines Parallel
Objective
Use the angles formed by a transversal
to prove two lines are parallel.
Holt Geometry
3-3 Proving Lines Parallel
What does x equal?
100
x
Holt Geometry
We don’t know
because we have no
idea if the lines are
parallel
3-3 Proving Lines Parallel
What does x equal?
100
x
Holt Geometry
Since the lines are
parallel, x=100.
3-3 Proving Lines Parallel
100
What do you know
about the lines?
They are not parallel.
25
Holt Geometry
3-3 Proving Lines Parallel
100
100
Holt Geometry
What do you know
about the lines?
The lines must be
parallel.
3-3 Proving Lines Parallel
Make an “if…then” statement about each figure’s angles and lines.
If two parallel lines are
cut by a transversal,
then the corresponding
angles are congruent.
100
100
Holt Geometry
Converse:
If two lines are cut by a
transversal so that the
corresponding angles are
congruent, then the lines are
parallel.
3-3 Proving Lines Parallel
Make an “if…then” statement about each figure’s angles and lines.
If two parallel lines are cut by
a transversal, then the
alternate interior angles are
congruent.
50
50
Holt Geometry
Converse:
If two lines are cut by a
transversal so that the
alternate interior angles are
congruent, then the lines are
parallel.
3-3 Proving Lines Parallel
Make an “if…then” statement about each figure’s angles and lines.
If two parallel lines are cut by
a transversal, then the
alternate exterior angles are
congruent.
60
60
Holt Geometry
Converse:
If two lines are cut by a
transversal so that the
alternate exterior angles are
congruent, then the lines are
parallel.
3-3 Proving Lines Parallel
Make an “if…then” statement about each figure’s angles and lines.
If two parallel lines are cut by
a transversal, then the
consecutive interior angles are
supplementary.
80
100
Holt Geometry
Converse:
If two lines are cut by a
transversal so that the
consecutive interior angles are
supplementary, then the lines
are parallel.
3-3 Proving Lines Parallel
Example 1A: Using the Converse of the
Corresponding Angles Postulate
Use the Converse of the Corresponding Angles
Postulate and the given information to show
that ℓ || m.
4  8
4  8
ℓ || m
Holt Geometry
4 and 8 are corresponding angles.
Conv. of Corr. s Post.
3-3 Proving Lines Parallel
Use the Converse of the Corresponding Angles
Postulate and the given information to show
that ℓ || m. (aka plug in the value of x and see
if it gives you a true statement.)
m3 = (4x – 80)°,
m7 = (3x – 50)°, x = 30
m3 = 4(30) – 80 = 40
m7 = 3(30) – 50 = 40
Substitute 30 for x.
Substitute 30 for x.
m3 = m7
3  7
ℓ || m
Trans. Prop. of Equality
Def. of  s.
Conv. of Corr. s Post.
Holt Geometry
3-3 Proving Lines Parallel
Check It Out! Example 1b
Use the Converse of the Corresponding Angles
Postulate and the given information to show
that ℓ || m.
m7 = (4x + 26)°,
m5 = (5x + 12)°, x = 13
m7 = 4(13) + 26 = 76
m5 = 5(13) + 12 = 77
m7 = m5
ℓ is not parallel to m
Holt Geometry
Substitute 13 for x.
Substitute 13 for x.
3-3 Proving Lines Parallel
Check It Out! Example 1b
Use the Converse of the Corresponding Angles
Postulate and the given information to show
that ℓ || m.
m2 = (3x + 10)°,
m3 = (5x + 10)°, x = 20
m2 = 3(20) + 10 = 70
m3 = 5(20) + 10 = 110
m2 + m3 = 180
70 + 110 = 180
ℓ || m
Holt Geometry
Substitute 13 for x.
Substitute 13 for x.
3-3 Proving Lines Parallel
Example 2B: Determining Whether Lines are Parallel
Use the given information and the theorems you
have learned to show that r || s.
m2 = (10x + 8)°,
m3 = (25x – 67)°, x = 5
m2 = 10x + 8
= 10(5) + 8 = 58
Substitute 5 for x.
m3 = 25x – 67
= 25(5) – 3 = 58
Substitute 5 for x.
Holt Geometry
3-3 Proving Lines Parallel
Example 2B Continued
Use the given information and the theorems you
have learned to show that r || s.
m2 = (10x + 8)°,
m3 = (25x – 67)°, x = 5
m2 + m3 = 58° + 58°
= 116°
2 and 3 are same-side
interior angles.
r is not parallel to s
Holt Geometry
3-3 Proving Lines Parallel
The Converse of the Corresponding Angles
Postulate is used to construct parallel lines.
The Parallel Postulate guarantees that for any
line ℓ, you can always construct a parallel line
through a point that is not on ℓ.
P
ℓ
Holt Geometry
3-3 Proving Lines Parallel
Example 4: Carpentry Application
A carpenter is creating a woodwork pattern
and wants two long pieces to be parallel.
m1= (8x + 20)° and m2 = (2x + 10)°.
If x = 15, show that pieces A and B are
parallel.
Holt Geometry
3-3 Proving Lines Parallel
Example 4 Continued
m1 = 8x + 20
= 8(15) + 20 = 140
Substitute 15 for x.
m2 = 2x + 10
= 2(15) + 10 = 40
m1+m2 = 140 + 40
= 180
Substitute 15 for x.
1 and 2 are
supplementary.
The same-side interior angles are supplementary, so
pieces A and B are parallel by the Converse of the
Same-Side Interior Angles Theorem.
Holt Geometry
3-3 Proving Lines Parallel
Check It Out! Example 4
What if…? Suppose the
corresponding angles on
the opposite side of the
boat measure (4y – 2)°
and (3y + 6)°, where
y = 8. Show that the oars
are parallel.
4y – 2 = 4(8) – 2 = 30°
3y + 6 = 3(8) + 6 =
30°
The angles are congruent, so the oars are || by the
Conv. of the Corr. s Post.
Holt Geometry