Download Vocabulary

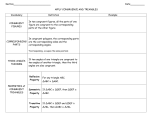
Vocabulary
Geometry
Spring 2013
UNDEFINED TERMS
Point – A point has no size. It is a position. It is identified by a capital letter:
•A
Line – A line is a collection of points that extends infinitely in two directions. It has no
width. It is represented by drawing a line with arrowheads on both ends, and it is
identified by naming two points on the line:
A
B
A line can also be identified with a single lower-case letter:
m
Plane – A plane is a flat surface that extends infinitely. It has no thickness. A plane is
usually represented by a four-sided figure like the one below, and it is identified with a
capital letter.
R
1
Vocabulary
Geometry
Spring 2013
BASIC DEFINITIONS
•
An Angle is formed when two rays have the same end-point. The rays are called the
sides of the angle, and the end-point is called the vertex. An angle is usually identified
with three letters representing a point on one side, the vertex, and a point on the other
A
∠ABC :
side.
C
B
•
Collinear Points are points that lie on the same line.
€
Coplanar Points are points that lie on the same plane.
•
Congruent line segments have the same length.
•
An Intersection is all of the points that two figures share.
•
A Line Segment (or segment) is a finite portion of a line.
•
A
B
•
Opposite Rays are two rays that form a straight line.
•
Parallel Lines never intersect.
•
Perpendicular Lines intersect to form four congruent angles.
•
A Ray is the portion of a line that starts at a point and continues infinitely in only one
direction.
•
B
A
A Segment Bisector is a line or segment that passes through the midpoint of the
segment, cutting it into two segments of equal length.
•
A Segment Midpoint is the same distance from each endpoint of the segment.
•
Space is the collection of all possible points.
•
A Transversal is a line that crosses two other lines.
•
A Vertex (plural: vertices) is the point where the sides of a figure connect.
2
€
Vocabulary
Geometry
Spring 2013
NOTATION
AB
the line that runs through points A and B
AB
the line segment with endpoints A and B
€
AB
the length of AB
€
AB
the ray that has the endpoint A and passes through point B
€
BA
€ that has the endpoint B and passes through point A
the ray
€
∠ABC
the angle formed by BA and BC
€
≅
"is congruent to" or "has the same measure as"
€
€
€
lines are parallel
segments are congruent
angles are congruent
3
Vocabulary
Geometry
Spring 2013
ANGLE DEFINITIONS
•
An Acute Angle has a measure that is less than 900.
•
vertex and do not overlap.
Adjacent Angles share a side and a vertex.
•
Alternate Interior Angles formed by a transversal are on opposite sides of the
transversal and on the inside of the two lines crossed by the transversal.
•
BD is the Angle Bisector of ∠ABC if point D lies in the interior of ∠ABC and ∠ABD is
congruent to ∠DBC .
€
•
€
€
€
Complementary Angles are two angles whose measures add up to ninety degrees.
€
•
Congruent angles have the same measure.
•
Corresponding angles formed by a transversal are in the same relative place in the
intersections created by the transversal as it crosses each line.
4
Vocabulary
Geometry
Spring 2013
ANGLE DEFINITIONS (continued )
•
A Linear Pair is made by two adjacent angles that form a straight line.
•
An Obtuse Angle has a measure that is greater than 900.
•
A Right Angle is congruent to the angles formed by perpendicular lines.
•
Same-side Interior Angles formed by a transversal are on the same side of the
transversal and on the inside of the two lines crossed by the transversal.
•
Supplementary Angles are two angles whose measures add up to one hundred eighty
degrees.
•
Vertical Angles are two angles whose sides form straight lines.
5
Vocabulary
Geometry
Spring 2013
CONDITIONAL STATEMENTS
Conditional:
"If p, then q."
p →q
Converse:
"If q, then p."
q →p
€
Inverse:
"If not p, then not q."
€
~ p →~ q
Contrapositive:
"If not q, then not p."
€
~ q →~ p
€
The conditional and contrapositive statements are equivalent.
€
€
The converse and inverse statements are equivalent.
6
Vocabulary
Geometry
Spring 2013
SHAPES
Area is the number of squares that can fit within a shape.
A circle is the collection of points that are all the same distance from a given point, called
the center of the circle.
A chord is a segment whose endpoints lie on a circle.
Circumference is the distance around the outside of a circle.
Congruent figures have the same size and shape.
The diameter is the distance from one point on a circle, through the center, to another point
on the circle.
The hypotenuse is the side opposite the right angle of a right triangle (and it is the longest
side).
A kite is a quadrilateral with two distinct pairs of congruent consecutive sides.
The perimeter is the distance around the outside of a polygon.
Pi (π ) is the ratio of the circumference to the diameter of any circle.
A polygon is a closed two-dimensional figure with straight sides.
A quadrilateral is a polygon with four sides.
The radius is the distance from the center of a circle to any point on the circle.
A rectangle is a quadrilateral with four right angles.
A rhombus is a quadrilateral with four congruent sides.
A secant is a line intersecting a circle at two points.
Similar figures have the same shape but are different sizes.
A square is a quadrilateral with four congruent sides and four right angles.
A tangent is a line intersecting a circle at exactly one point.
A trapezoid is a quadrilateral with at least one pair of parallel lines.
Volume is the number of cubes that can fit inside a three-dimensional shape.
7
Vocabulary
Geometry
Spring 2013
ANGLE RELATIONSHIP VOCABULARY
•
Corresponding angles formed by a transversal crossing parallel lines are congruent.
•
Corresponding angles of similar triangles are congruent.
•
The measures of adjacent angles formed when two lines cross add up to 180
degrees.
•
The measures of alternate interior angles formed when a transversal crosses two
lines are not necessarily related.
•
The measures of angles forming a linear pair add up to 180 degrees.
•
The measures of same-side interior angles formed by a transversal crossing parallel
lines add up to 180 degrees.
•
The measures of the angles of a triangle add up to 180 degrees.
•
Vertical angles are congruent.
8
€
Vocabulary
Geometry
Spring 2013
TRIANGLE SIMILARITY
Two triangles are similar if and only if all three pairs of corresponding angles are congruent
and the ratios of all three pairs of corresponding sides are equal.
ΔABC and ΔXYZ are similar. List everything you know about the angles and
sides of these two triangles. Be specific and clear.
1. All the corresponding pairs of sides have a common ratio:
€
AB
=r
XY
BC
=r
YZ
AC
=r
XZ
2. All the corresponding angles are congruent:
€
∠ABC ≅ ∠XYZ ;
∠BCA ≅ ∠YZX ;
∠BAC ≅ ∠YXZ
€
€
€
9
Vocabulary
Geometry
Spring 2013
List three short cuts you can use to show that two triangles are similar. Draw an
example of each, and clearly label only the sides and/or angles required to model
your situation.
€
€
€
1. SSS ~ (Side-Side-Side) -- If you
show that all three pairs of correspondingx
sides share a common ratio, then the
triangles are similar and the
corresponding angles are congruent.
2. SAS ~ (Side-Angle-Side) -- If you
show that two pairs of corresponding
sides share a common ratio and the
angles between them are congruent, then
the triangles are similar and the other two
pairs of corresponding angles are
congruent and the remaining pair of sides
share the same common ratio.
z
x•r
z•r
y•r
y
z
y
z•r
y•r
3. AA ~ (Angle-Angle) -- If you show
that two pairs of corresponding angles are
congruent, the triangles are similar, which
means the remaining pair of corresponding
angles is congruent and all three pairs of
corresponding sides share a common
ratio.
*NOTE: “Similar” is not used to describe pairs of angles or pairs of sides. Such pairs are either “congruent,”
or they are not. The sides of similar triangles are said to share a common ratio – that is, the quotient of each
pair of corresponding sides is the same.
10
Vocabulary
Geometry
Spring 2013
Given two sides of a triangle with lengths x and y, what does the triangle inequality
theorem tell you about z, the length of the third side?
The length of the third side of a triangle must be greater than the absolute value of the
difference of the lengths of the two other sides.
z> x−y
The length of the third side of a triangle must also be less than the sum of the lengths of
the other two sides.
z<x+y
€
€
Exterior Angle (of a triangle)
yo
xo
zo = xo + yo
zo
The sum of two interior angles of a triangle is equal to the exterior angle of the third angle
of the triangle.
11
Vocabulary
Geometry
Spring 2013
Use conditional statements to identify ways you can use angles to demonstrate that
two lines are parallel:
1. If alternate interior/exterior angles formed by a transversal crossing two lines are
congruent, then the lines are parallel.
2. If corresponding angles formed by a transversal crossing two lines are congruent, then
the lines are parallel.
3. If same-side interior angles formed by a transversal crossing two lines are
supplementary, then the lines are parallel.
Use a full sentence to write a definition for each of the following terms:*
Complementary Angles are two angles whose measures add up to 90 degrees.
Supplementary Angles are two angles whose measures add up to 180 degrees.
A Diagonal is a line segment that connects two vertices of a polygon but is not a side.
A Vertex is the place where two or more line segments or rays meet to form a corner, such
as in a polygon or an angle. (Vertices is the plural of vertex.)
A Linear Pair is a pair of adjacent angles whose opposite sides form a straight line.
Vertical Angles are the opposite (i.e., the non-adjacent) angles formed by two intersecting
lines, or they are two angles whose sides form straight lines.
What is the base angle theorem?
The angles opposite the two congruent sides of an isosceles triangle are congruent.
What is the triangle inequality theorem?
The sum of the lengths of any two sides of a triangle is always greater than the length of
the remaining side.
What is the triangle angle sum theorem?
The sum of the measures of the angles of a triangle is always 180 degrees.
What is the Pythagorean theorem?
In a right triangle, the square of the length of the hypotenuse is equal to the sum of the
squares of the lengths of the legs.
12