Document
... In the Language of Algebra, an equation is the basic number "sentence". An equation is a mathematical expression that contains an equals sign. An equation can contain variables represented by letters ...
... In the Language of Algebra, an equation is the basic number "sentence". An equation is a mathematical expression that contains an equals sign. An equation can contain variables represented by letters ...
Geometric Numbers
... Exactly like a multiplication chart, we can use the same idea for square numbers! Notice how the square numbers line up along the diagonal… ...
... Exactly like a multiplication chart, we can use the same idea for square numbers! Notice how the square numbers line up along the diagonal… ...
Exam Review Topics
... Solving Linear Equations - using addition and subtraction - using multiplication and division Questions to ask yourself: 1. What is being done to the variable? 2. How can I “un-do” that? 3. Perform operation. 4. Check solution. Solving Multi-step equations (work backward through the Order of Operati ...
... Solving Linear Equations - using addition and subtraction - using multiplication and division Questions to ask yourself: 1. What is being done to the variable? 2. How can I “un-do” that? 3. Perform operation. 4. Check solution. Solving Multi-step equations (work backward through the Order of Operati ...
File - Mrs. Hille`s FunZone
... the number of possible milkshakes that could be ordered if chocolate and vanilla shakes are available in small, medium, and large. ...
... the number of possible milkshakes that could be ordered if chocolate and vanilla shakes are available in small, medium, and large. ...
10_lecture_20100216_Arrays3
... Solve for {X,Y,Z} that satisfies both equations simultaneously! What would be A and b? ...
... Solve for {X,Y,Z} that satisfies both equations simultaneously! What would be A and b? ...
Guided notes: Scientific notation
... ADDING or SUBTRACTING in scientific notation 1. First make sure that the numbers are written in the same form (have the same exponent) 3.2 x 103 + 40 x 102 (change to 4.0 x 103) 2. Add (or subtract) first part of exponent (mantissas) ...
... ADDING or SUBTRACTING in scientific notation 1. First make sure that the numbers are written in the same form (have the same exponent) 3.2 x 103 + 40 x 102 (change to 4.0 x 103) 2. Add (or subtract) first part of exponent (mantissas) ...
Objective - OnCourse
... Find the difference (subtract) their absolute values. The result has the sign of the number with largest absolute value Ex) -10 + 3 = -7 ...
... Find the difference (subtract) their absolute values. The result has the sign of the number with largest absolute value Ex) -10 + 3 = -7 ...
Enfield LA Mental Calculation Guidance
... Numbers and the number system Count in steps of 2, 3, and 5 from 0, and in tens from any number, forward and backward Recognise the place value of each digit in a two-digit number (tens, ones) Identify, represent and estimate numbers using different representations, including the number line Compare ...
... Numbers and the number system Count in steps of 2, 3, and 5 from 0, and in tens from any number, forward and backward Recognise the place value of each digit in a two-digit number (tens, ones) Identify, represent and estimate numbers using different representations, including the number line Compare ...
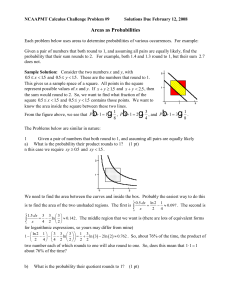
NCAAPMT Calculus Challenge Problem #9 Solutions Due February
... triangles below y = x are the same. If the ratio is less than one, then the first non-zero digits are uniformly distributed. However, if the ratio is larger than one, things get more interesting. Notice how much larger the region between y = x and y = 2x (in blue) is than the region between y = 5x a ...
... triangles below y = x are the same. If the ratio is less than one, then the first non-zero digits are uniformly distributed. However, if the ratio is larger than one, things get more interesting. Notice how much larger the region between y = x and y = 2x (in blue) is than the region between y = 5x a ...
Number # Significant Digits
... There are two kinds of numbers Counted or defined - exact, not subject to estimate. Ex: number of eggs in a carton. Measured - always carries some amount of uncertainty because measurement involves estimation. The size of uncertainty depends on the precision of the measuring device AND the skill ...
... There are two kinds of numbers Counted or defined - exact, not subject to estimate. Ex: number of eggs in a carton. Measured - always carries some amount of uncertainty because measurement involves estimation. The size of uncertainty depends on the precision of the measuring device AND the skill ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.