FTCE Middle Grades Math 5-9 Competency 8
... Cone - cone has one circular base and a vertex that is not on the base. Sphere – all points on the sphere are equidistant from the center. ...
... Cone - cone has one circular base and a vertex that is not on the base. Sphere – all points on the sphere are equidistant from the center. ...
Circles Packet
... A segment whose endpoints are the center of the circle and the perimeter of the circle Chord – a segment whose endpoints both lie on the circle (“on the circle” means on the perimeter) Secant – a line that contains points on the interior of a circle as well as the exterior (a line that runs through ...
... A segment whose endpoints are the center of the circle and the perimeter of the circle Chord – a segment whose endpoints both lie on the circle (“on the circle” means on the perimeter) Secant – a line that contains points on the interior of a circle as well as the exterior (a line that runs through ...
The degree measure of an arc is
... A tangent segment is a line segment from the point of tangency to another point on the tangent line. Theorem: Two tangent segments drawn to a circle from the same external point ...
... A tangent segment is a line segment from the point of tangency to another point on the tangent line. Theorem: Two tangent segments drawn to a circle from the same external point ...
Part I: Parts of a Circle
... Outcome: SS7.1 Demonstrate an understanding of circles, including circumference and central angles. ...
... Outcome: SS7.1 Demonstrate an understanding of circles, including circumference and central angles. ...
Mathematics Chapter: Tangents to Circles - JSUNIL tutorial
... Again, the length of common internal tangent to these two circles is 7 units. We can draw it as – ...
... Again, the length of common internal tangent to these two circles is 7 units. We can draw it as – ...
Lap 6 Definitions and Conjectures Congruent Circles: Two or more
... Congruent Circles: Two or more circles with congruent radii. Concentric Circles: Two or more circles sharing the same center. Radius: A segment with one endpoint the center of the circle and the other one on the circle. Chord: A segment with endpoints on the circle (The diameter IS a chord). Diamete ...
... Congruent Circles: Two or more circles with congruent radii. Concentric Circles: Two or more circles sharing the same center. Radius: A segment with one endpoint the center of the circle and the other one on the circle. Chord: A segment with endpoints on the circle (The diameter IS a chord). Diamete ...
Standards Framework Template
... bisector, and perpendicular bisector. (K) I can construct the inscribed circle whose center is the point of intersection of the angle bisectors (the incenter).(P) I can construct the circumscribed circle whose center is the point of intersection of the perpendicular bisectors of each side of the tri ...
... bisector, and perpendicular bisector. (K) I can construct the inscribed circle whose center is the point of intersection of the angle bisectors (the incenter).(P) I can construct the circumscribed circle whose center is the point of intersection of the perpendicular bisectors of each side of the tri ...
Circles
... o Tangents to same circle are congruent. o Tangents cross circle at 1 point whereas secants cross at 2. o Inscribed polygons are polygons within a circle with all vertices on the circle whereas circumscribed polygons are polygons that surround a circle with the circle touching all sides of the polyg ...
... o Tangents to same circle are congruent. o Tangents cross circle at 1 point whereas secants cross at 2. o Inscribed polygons are polygons within a circle with all vertices on the circle whereas circumscribed polygons are polygons that surround a circle with the circle touching all sides of the polyg ...
Geometry—Segment 2 Reference Sheet
... figures are congruent and the height of the figures is also congruent, then it can be concluded that the volumes of the two figures are congruent. ...
... figures are congruent and the height of the figures is also congruent, then it can be concluded that the volumes of the two figures are congruent. ...
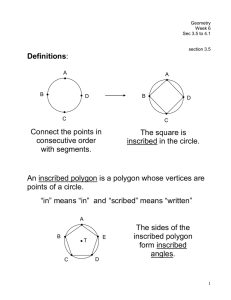
Definitions: An inscribed polygon is a polygon whose vertices are
... 2. Lines and compass marks should look like eyelashes on the paper. These marks represent lines that have no width, so make the representations believable. Make light marks that can be erased if necessary. 3. Be neat. Carefully align your arcs and lines to pass through the correct points. Also, do n ...
... 2. Lines and compass marks should look like eyelashes on the paper. These marks represent lines that have no width, so make the representations believable. Make light marks that can be erased if necessary. 3. Be neat. Carefully align your arcs and lines to pass through the correct points. Also, do n ...
Math 90 Unit 8 – Circle Geometry
... 8.1 – Properties of Tangents to a Circle Investigate: Page 384 A line that intersects a circle at only one point is a tangent to the circle. The point where the tangent intersects the circle is the point of tangency. For example: Line AB is a tangent to the circle with center O. Point P is the point ...
... 8.1 – Properties of Tangents to a Circle Investigate: Page 384 A line that intersects a circle at only one point is a tangent to the circle. The point where the tangent intersects the circle is the point of tangency. For example: Line AB is a tangent to the circle with center O. Point P is the point ...
Term 2 - Summative Assessment
... 20. Rohit, who is on a tour, has Rs 360 for his expenses. If he extends his tour for four days, he has to cut down his daily expenses by Rs 3. Find the original duration of the tour. 21. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 12 cm and 16 cm. Now construct an ...
... 20. Rohit, who is on a tour, has Rs 360 for his expenses. If he extends his tour for four days, he has to cut down his daily expenses by Rs 3. Find the original duration of the tour. 21. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 12 cm and 16 cm. Now construct an ...
Tangent lines to circles
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Roughly speaking, it is a line through a pair of infinitely close points on the circle. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.