Geometry – Circles ~1~ NJCTL.org
... Conceptual Category: Geometry Domain: Circles Cluster: Understand and apply theorems about circles. Standard#: Standard: Prove that all circles are similar. G-C.1 G-C.2 ...
... Conceptual Category: Geometry Domain: Circles Cluster: Understand and apply theorems about circles. Standard#: Standard: Prove that all circles are similar. G-C.1 G-C.2 ...
Circle Geometry - Overflow Education
... A chord is a line segment joining any two points on the circle. Divides circle into two parts, the minor arc and major arc. Secant A secant is a line that goes through a circle. Sector A sector is the region between two radii and the arc cut off by these radii. Segment A segment is the region betw ...
... A chord is a line segment joining any two points on the circle. Divides circle into two parts, the minor arc and major arc. Secant A secant is a line that goes through a circle. Sector A sector is the region between two radii and the arc cut off by these radii. Segment A segment is the region betw ...
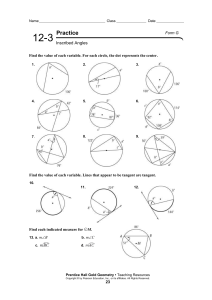
10. 4 Other Angle Relationships in Circles - Geometry 10-12
... There are 3 theorems you will use to solve for missing angles or arcs in a circle. You choose which theorem to use based on where 2 lines intersect. In other words, determine whether the intersection is: ...
... There are 3 theorems you will use to solve for missing angles or arcs in a circle. You choose which theorem to use based on where 2 lines intersect. In other words, determine whether the intersection is: ...
Circle
... Circle – set of all points _________ equidistant from a given point called the _____ center of the circle. Symbol: ...
... Circle – set of all points _________ equidistant from a given point called the _____ center of the circle. Symbol: ...
4.1 - CCGPS Geometry
... Circle – set of all points _________ equidistant from a given point called the _____ center of the circle. Symbol: ...
... Circle – set of all points _________ equidistant from a given point called the _____ center of the circle. Symbol: ...
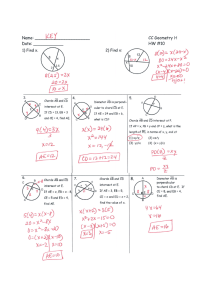
Answers for the lesson “Find Segment Lengths in Circles”
... (Two points determine a line.) 3. ACD > ABD, �CAB > �CDB (If two inscribed angles of a circle intercept the same arc, then the angles are congruent.) ...
... (Two points determine a line.) 3. ACD > ABD, �CAB > �CDB (If two inscribed angles of a circle intercept the same arc, then the angles are congruent.) ...
Chapter 6 Learning Objectives
... 1. become familiar with the terminology (radius, center, chord, are, etc.) of the circle; 2. state/apply postulates related to the circle; 3. state/apply/prove selected theorems related to the circle; and 4. state/apply methods of measuring central and inscribed angles in the circle. Section 6.2: Mo ...
... 1. become familiar with the terminology (radius, center, chord, are, etc.) of the circle; 2. state/apply postulates related to the circle; 3. state/apply/prove selected theorems related to the circle; and 4. state/apply methods of measuring central and inscribed angles in the circle. Section 6.2: Mo ...
Tangent and Chord Properties
... Diameter- chord that goes through the center of the circle Tangent – segment or line that touches the circle at one point Central Angle – is the angle formed by 2 radii at the center of the circle Minor Arc – arc formed between 2 radii, measured in degrees Major Arc – larger arc formed by 2 radii Se ...
... Diameter- chord that goes through the center of the circle Tangent – segment or line that touches the circle at one point Central Angle – is the angle formed by 2 radii at the center of the circle Minor Arc – arc formed between 2 radii, measured in degrees Major Arc – larger arc formed by 2 radii Se ...
Tangent lines to circles
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Roughly speaking, it is a line through a pair of infinitely close points on the circle. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.