Geometry 4th Nine Weeks Scope and
... (28) Derive, using similarity, the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. [G-C5] (29) Derive the equation of a circle of given c ...
... (28) Derive, using similarity, the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. [G-C5] (29) Derive the equation of a circle of given c ...
Chapter 10: Circles
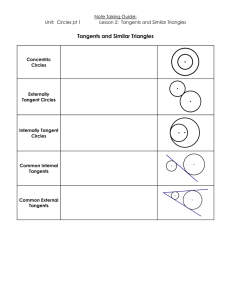
... angles are supplementary If a radius or diameter is perpendicular to a chord, it bisects the chord and its arc If two chords are equidistant from the center of the circle, the chords are congruent ...
... angles are supplementary If a radius or diameter is perpendicular to a chord, it bisects the chord and its arc If two chords are equidistant from the center of the circle, the chords are congruent ...
Act. 4.3: Angles Formed by Chords, Tangents and Secants
... A chord is a line segment with both endpoints on the circle A tangent is a line that touches the circle at one point N (the “point of tangency”) D R ...
... A chord is a line segment with both endpoints on the circle A tangent is a line that touches the circle at one point N (the “point of tangency”) D R ...
Units_007-090 FV - Pearson Schools and FE Colleges
... (c) Opposite angles of a cyclic quadrilateral are supplementary. (d) The exterior angle of a cyclic quadrilateral equals the interior opposite angle. (a) ...
... (c) Opposite angles of a cyclic quadrilateral are supplementary. (d) The exterior angle of a cyclic quadrilateral equals the interior opposite angle. (a) ...
2 - Campbell County, TN Public Schools
... G.GPE.B.4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point ( ...
... G.GPE.B.4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point ( ...
Geometry Level 1 Curriculum
... of a circle 3. If a radius is perp to a chord, then it bisects the chord (and the converse) 4. The perp. bisector of a chord passes through the center of the circle 5. Vocabulary: sector, circle, center, radius, concentric, interior, exterior, diameter, chord, arc, central angle, minor arc, major ar ...
... of a circle 3. If a radius is perp to a chord, then it bisects the chord (and the converse) 4. The perp. bisector of a chord passes through the center of the circle 5. Vocabulary: sector, circle, center, radius, concentric, interior, exterior, diameter, chord, arc, central angle, minor arc, major ar ...
Circle Chapter
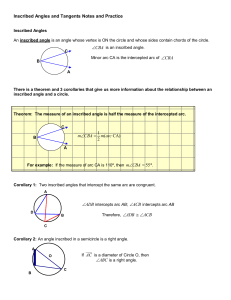
... Angle formed by a tangent and a radii or diameter form a right angle on the edge of a circle. Two inscribed angles that intercept the same arc are congruent. Angles formed outside the circle equal ½ the difference of the two arcs that it intercepts The angle can be formed by either 2 tangents, 2 sec ...
... Angle formed by a tangent and a radii or diameter form a right angle on the edge of a circle. Two inscribed angles that intercept the same arc are congruent. Angles formed outside the circle equal ½ the difference of the two arcs that it intercepts The angle can be formed by either 2 tangents, 2 sec ...
Circles REVIEW
... If a quadrilateral is inscribed in a circles, then its opposite angles are supplementary. ...
... If a quadrilateral is inscribed in a circles, then its opposite angles are supplementary. ...
Geometry Unit 7 Test Review Target 2: I can use definitions
... Target 4: I understand that the radius of a circle is perpendicular to the tangent where the radius intersects the circle. G.C.2 ...
... Target 4: I understand that the radius of a circle is perpendicular to the tangent where the radius intersects the circle. G.C.2 ...
week6
... A tangent line (or tangent) is a line in the planed of a circle that intersects the circle in exactly one point. The point of tangency is the point at which a tangent line and a circle intersect. A tangent segment is a segment of a tangent line that contains the point of tangency. tangent segments: ...
... A tangent line (or tangent) is a line in the planed of a circle that intersects the circle in exactly one point. The point of tangency is the point at which a tangent line and a circle intersect. A tangent segment is a segment of a tangent line that contains the point of tangency. tangent segments: ...
Tangent lines to circles
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Roughly speaking, it is a line through a pair of infinitely close points on the circle. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.