5. Circles and lines 5.1. Circles. A circle Σ is the set of points at fixed
... 5.1. Circles. A circle Σ is the set of points at fixed distance r > 0 from a given point, its center. The distance r is called the radius of the circle Σ. The circle Σ divides the plane into two regions: the inside, which is the set of points at distance less than r from the center O, and the outsid ...
... 5.1. Circles. A circle Σ is the set of points at fixed distance r > 0 from a given point, its center. The distance r is called the radius of the circle Σ. The circle Σ divides the plane into two regions: the inside, which is the set of points at distance less than r from the center O, and the outsid ...
SMART Notebook - Manhasset Schools
... e. If m≮7 = 125 and m≮3 = 35, find m≮4. 900 5. In the figure to the right, CD bisects ≮ACB, ...
... e. If m≮7 = 125 and m≮3 = 35, find m≮4. 900 5. In the figure to the right, CD bisects ≮ACB, ...
Type Grade Here
... Unit 3 – Circles and Volume MCC9-12.G.C.1 Prove that all circles are similar. 1. Given a circle of a radius of 3 and another circle with a radius of 5, compare the ratios of the two radii, the two diameters, and the two circumferences. 2. What is the ratio of circumference to diameter of any circle? ...
... Unit 3 – Circles and Volume MCC9-12.G.C.1 Prove that all circles are similar. 1. Given a circle of a radius of 3 and another circle with a radius of 5, compare the ratios of the two radii, the two diameters, and the two circumferences. 2. What is the ratio of circumference to diameter of any circle? ...
Quarter 3
... G-CO.D.13 Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. Topic 15 ...
... G-CO.D.13 Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. Topic 15 ...
GCSE Circles website File - Beverley High School VLE
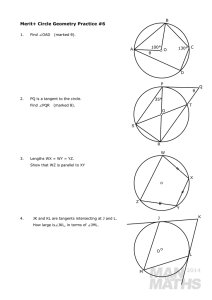
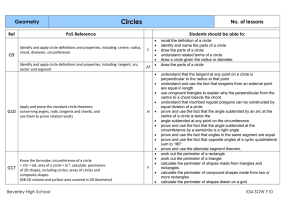
... understand that the tangent at any point on a circle is perpendicular to the radius at that point understand and use the fact that tangents from an external point are equal in length use congruent triangles to explain why the perpendicular from the centre to a chord bisects the chord understand that ...
... understand that the tangent at any point on a circle is perpendicular to the radius at that point understand and use the fact that tangents from an external point are equal in length use congruent triangles to explain why the perpendicular from the centre to a chord bisects the chord understand that ...
learning progression 1
... When it comes to circles, students often think that they don't have to worry about angles anymore. After all, a circle is a curve. Before students can identify and describe the various angles in a circle, they should be familiar with what these angles are. Students should also be familiar with the c ...
... When it comes to circles, students often think that they don't have to worry about angles anymore. After all, a circle is a curve. Before students can identify and describe the various angles in a circle, they should be familiar with what these angles are. Students should also be familiar with the c ...
document
... Two circles are internally tangent if both are on the same side of the common tangent line Two circles are externally tangent if the circles are on opposite sides of the common tangent line If two circles are either internally or externally tangent, a line connecting the centers of the circles passe ...
... Two circles are internally tangent if both are on the same side of the common tangent line Two circles are externally tangent if the circles are on opposite sides of the common tangent line If two circles are either internally or externally tangent, a line connecting the centers of the circles passe ...
Bisect a Line
... given distance Across Corners (Inscribed) Given distance AB across the corners, draw a circle with AB as the diameter With A and B as centers and the same radius, draw arcs to intersect the circle at points C, D, E, and F Connect the points to complete the hexagon ...
... given distance Across Corners (Inscribed) Given distance AB across the corners, draw a circle with AB as the diameter With A and B as centers and the same radius, draw arcs to intersect the circle at points C, D, E, and F Connect the points to complete the hexagon ...
Common Core Geometry Critical Area 4: Circles
... A. Understand and apply theorems about circles 1. Prove that all circles are similar. 2. Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed and circumscribed angles; inscribed angles ...
... A. Understand and apply theorems about circles 1. Prove that all circles are similar. 2. Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed and circumscribed angles; inscribed angles ...
Tangent lines to circles
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Roughly speaking, it is a line through a pair of infinitely close points on the circle. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.