Unit 3 Review File - Northwest ISD Moodle
... 13. Write the equation of a line parallel to a line containing the two points (4, -2) and (5, -8) and crosses through the point (1, 0). -8 – (-2) = -6 = -6 m = -6 0 = -6(1) + b ...
... 13. Write the equation of a line parallel to a line containing the two points (4, -2) and (5, -8) and crosses through the point (1, 0). -8 – (-2) = -6 = -6 m = -6 0 = -6(1) + b ...
Mod 5 - Aim #11 - Manhasset Schools
... At 5:00, the observer in the lighthouse measured the angle of depression to the front of the canoe to be 6°. Five minutes later, the observer measured and saw the angle of depression to the front of the canoe had increased by 49°. Determine and state, to the nearest foot per minute, the average spee ...
... At 5:00, the observer in the lighthouse measured the angle of depression to the front of the canoe to be 6°. Five minutes later, the observer measured and saw the angle of depression to the front of the canoe had increased by 49°. Determine and state, to the nearest foot per minute, the average spee ...
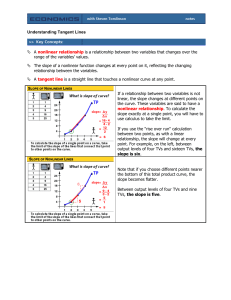
Understanding Tangent Lines A nonlinear relationship is a
... A nonlinear relationship is a relationship between two variables that changes over the range of the variables' values. The slope of a nonlinear function changes at every point on it, reflecting the changing relationship between the variables. A tangent line is a straight line that touches a nonlinea ...
... A nonlinear relationship is a relationship between two variables that changes over the range of the variables' values. The slope of a nonlinear function changes at every point on it, reflecting the changing relationship between the variables. A tangent line is a straight line that touches a nonlinea ...
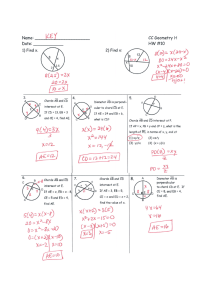
Name
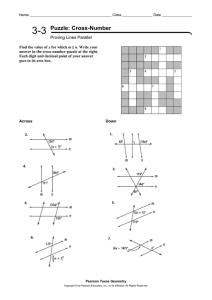
... Identify angle relationships (e.g. corresponding) when two lines (not parallel) are intersected by a transversal (3.1) Identify parallel, perpendicular and skew lines and parallel planes given in a diagram Complete a flow proof by adding reasons for each statement (3-2) Perpendicular Line Th ...
... Identify angle relationships (e.g. corresponding) when two lines (not parallel) are intersected by a transversal (3.1) Identify parallel, perpendicular and skew lines and parallel planes given in a diagram Complete a flow proof by adding reasons for each statement (3-2) Perpendicular Line Th ...
Montclair Public Schools CCSS Geometry Honors Unit: Marshall A.b
... Inductive and deductive reasoning are used to prove valid geometric statement true. Geometric constructions help students discover and explore geometric concepts and interpret geometric concepts. Parallel line properties (CA, AIA, SSIA, AEA and their converses) can be used to find missing angles and ...
... Inductive and deductive reasoning are used to prove valid geometric statement true. Geometric constructions help students discover and explore geometric concepts and interpret geometric concepts. Parallel line properties (CA, AIA, SSIA, AEA and their converses) can be used to find missing angles and ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.