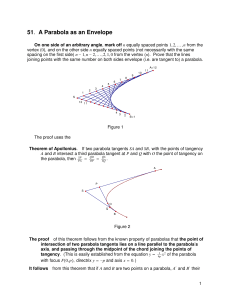
Geometry Student Project Material Outline
... -Explain that if a tangent and a secant intersect at a point of tangency that the angle formed is half of the intercepted arc. -Explain that the angle formed by 2 secants outside a circle is half of the difference of the intercepted arcs. -Explain that the angle formed by 2 secants inside a circle i ...
... -Explain that if a tangent and a secant intersect at a point of tangency that the angle formed is half of the intercepted arc. -Explain that the angle formed by 2 secants outside a circle is half of the difference of the intercepted arcs. -Explain that the angle formed by 2 secants inside a circle i ...
Geometry_Definitions-Learn_these
... Implies is a term we use in a proof when we can write down a fact we have proved from a previous statement. Symbol is => 7. Transversal A transversal is a line which cuts two or more parallel lines 8. A Vertex A vertex is where two lines meet to form an angle ...
... Implies is a term we use in a proof when we can write down a fact we have proved from a previous statement. Symbol is => 7. Transversal A transversal is a line which cuts two or more parallel lines 8. A Vertex A vertex is where two lines meet to form an angle ...
1-10=working with new vocab transversals
... 15. Visualization If two planes are parallel, must all lines within those planes be parallel? ...
... 15. Visualization If two planes are parallel, must all lines within those planes be parallel? ...
Geometry Review - lowesgeometryprojects
... hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other ...
... hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other ...
AMS (Mos) SUBJECT CLASSIFICATION CODES. Primary: 46A12
... An F--semi-norm on E is a mapping v" E- such that x) _> 0 for all x E E; (i) ,lx) _< x) for x E d for [[ 1; (ii) x+y) x) + y) for x, y E; (iii) for each x e E, g(]x) 0 ] 0. ...
... An F--semi-norm on E is a mapping v" E- such that x) _> 0 for all x E E; (i) ,lx) _< x) for x E d for [[ 1; (ii) x+y) x) + y) for x, y E; (iii) for each x e E, g(]x) 0 ] 0. ...
A. True/False: Given ∥ in the diagram below, determine whether
... Geometry Parallel Lines QR Review ...
... Geometry Parallel Lines QR Review ...
Plines
... Two parallel lines on their own are not vary interesting to us in terms of geometry. But if straight line (called a transversal) intersects two parallel lines, then the angles created are very interesting to us….. ...
... Two parallel lines on their own are not vary interesting to us in terms of geometry. But if straight line (called a transversal) intersects two parallel lines, then the angles created are very interesting to us….. ...
2.6.1 Parallel Lines without a Parallel Postulate
... 1. Let M be the midpoint of segment BC. 2. B-M-C and 3. There is a point E on ray AM such that A-M-E and ME = MA. ...
... 1. Let M be the midpoint of segment BC. 2. B-M-C and 3. There is a point E on ray AM such that A-M-E and ME = MA. ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.