Unit #3 Review File - Northwest ISD Moodle
... 12. What would be an equation of a line perpendicular to 4x – 2y = 12 passing through point (-1,5)? ...
... 12. What would be an equation of a line perpendicular to 4x – 2y = 12 passing through point (-1,5)? ...
geometry-chapter-3-review
... determine which lines, if any, must be parallel. If any lines are parallel, use a theorem or postulate to tell why. ...
... determine which lines, if any, must be parallel. If any lines are parallel, use a theorem or postulate to tell why. ...
Geometry Fall 2013 Topics
... b. Pyramids c. Cylinders and Cones d. Spheres e. Surface areas and volumes of similar solids f. Cavalieri’s Principle g. Identify the shapes of 2-D cross-sections of 3-D objects, and identify 3-D objects generated by rotations of 2-D objects. 16. Transformations a. Reflections b. Translations and Gl ...
... b. Pyramids c. Cylinders and Cones d. Spheres e. Surface areas and volumes of similar solids f. Cavalieri’s Principle g. Identify the shapes of 2-D cross-sections of 3-D objects, and identify 3-D objects generated by rotations of 2-D objects. 16. Transformations a. Reflections b. Translations and Gl ...
Geometry Semester Exam
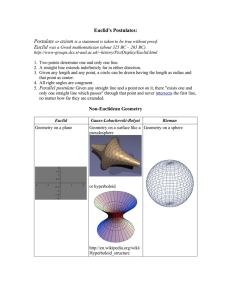
... case in Euclidean geometry. Which best explains the reason why this is true? ...
... case in Euclidean geometry. Which best explains the reason why this is true? ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.