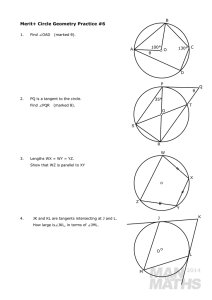
Parallelograms (part 2)
... Ø Show both pairs of opposite sides are parallel. Ø Show both pairs of opposite sides are congruent. Ø Show both pairs of opposite angles are congruent. Ø Show one angle is supplementary to both consecutive angles. Ø Show the diagonals bisect each other. Ø Show one pair of opposite sides ...
... Ø Show both pairs of opposite sides are parallel. Ø Show both pairs of opposite sides are congruent. Ø Show both pairs of opposite angles are congruent. Ø Show one angle is supplementary to both consecutive angles. Ø Show the diagonals bisect each other. Ø Show one pair of opposite sides ...
Pre-AP Geometry 7.7 HW – Applying Trig Ratios to solve Right
... 19. What angles have nearly the same sine and tangent 20. What angle has the greatest difference in its sine and value? tangent value? Use your 10cm circle to explain why that is the case. ...
... 19. What angles have nearly the same sine and tangent 20. What angle has the greatest difference in its sine and value? tangent value? Use your 10cm circle to explain why that is the case. ...
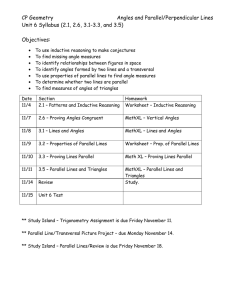
CP Geometry Angles and Parallel/Perpendicular Lines Unit 6 Syllabus
... To use inductive reasoning to make conjectures To find missing angle measures To identify relationships between figures in space To identify angles formed by two lines and a transversal To use properties of parallel lines to find angle measures To determine whether two lines are parallel To find mea ...
... To use inductive reasoning to make conjectures To find missing angle measures To identify relationships between figures in space To identify angles formed by two lines and a transversal To use properties of parallel lines to find angle measures To determine whether two lines are parallel To find mea ...
5 Minute Check, 26 Sep
... Essential Question: What are parallel lines, skew lines, and transversals and how can I use them? ...
... Essential Question: What are parallel lines, skew lines, and transversals and how can I use them? ...
Lesson 1 Contents
... Substitute the given angle measures into this equation and solve for x. Once you know the value of x, use ...
... Substitute the given angle measures into this equation and solve for x. Once you know the value of x, use ...
Distribution of Lessons / Units for self
... dated 03.05.2016, the lessons / units chosen for self study in the subject of Mathematics, during ensuing Summer Vacation 2016-17 by students of class IX, X and XII are detailed as below. As such, you are requested to inform the students accordingly. ...
... dated 03.05.2016, the lessons / units chosen for self study in the subject of Mathematics, during ensuing Summer Vacation 2016-17 by students of class IX, X and XII are detailed as below. As such, you are requested to inform the students accordingly. ...
Blank UbD Planning Template
... Why is it important to our society? 2. Where do you see geometric figures in daily life and how are they important? 3. Why is measuring lengths and angles precisely important to society? Students will be able to … 1 Find the lengths and midpoints of line segments in one- or two-dimensional coordinat ...
... Why is it important to our society? 2. Where do you see geometric figures in daily life and how are they important? 3. Why is measuring lengths and angles precisely important to society? Students will be able to … 1 Find the lengths and midpoints of line segments in one- or two-dimensional coordinat ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.