Geometry Unit 1 Intro to Geometry Chapter 3 Parallel Lines
... G-CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angels are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant ...
... G-CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angels are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant ...
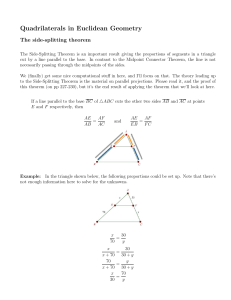
Notes on the Side-Splitting Theorem
... Example: (don’t do this!) Although there is a proportional relationship between the marked side lengths EF and BC, it is not the same as the other proportions. Do not ever set up the proportions shown on the screen and marked with a big red X. ...
... Example: (don’t do this!) Although there is a proportional relationship between the marked side lengths EF and BC, it is not the same as the other proportions. Do not ever set up the proportions shown on the screen and marked with a big red X. ...
l - UNT College of Engineering
... geometry of the lattice •When computing distances, angles and interplanar spacings in lattices, it is important to remember that Bravais lattice basis vectors are not always mutually orthogonal. •There are generalized rules for computing the geometric characteristics of lattices, applicable to all 7 ...
... geometry of the lattice •When computing distances, angles and interplanar spacings in lattices, it is important to remember that Bravais lattice basis vectors are not always mutually orthogonal. •There are generalized rules for computing the geometric characteristics of lattices, applicable to all 7 ...
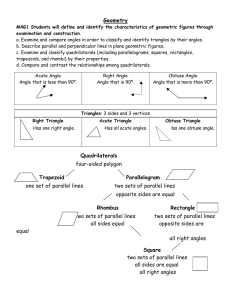
honors geometry—chapter 3—test review
... diagram? For each conclusion, provide the justification. _____________________________ ...
... diagram? For each conclusion, provide the justification. _____________________________ ...
A GENERALLY COVARIANT FIELD EQUATION FOR GRAVITATION
... 4. M. W. Evans and L. B. Crowell, Classical and Quantum Electrodynamics and the B (3) Field (World Scientific, Singapore, 2001). 5. M. W. Evans and A. A. Hasanein, The Photomagneton in Quantum Field Theory (World Scientific, Singapore, 1994). 6. M. W. Evans and S. Kielich, eds., Modern Non-Linear Op ...
... 4. M. W. Evans and L. B. Crowell, Classical and Quantum Electrodynamics and the B (3) Field (World Scientific, Singapore, 2001). 5. M. W. Evans and A. A. Hasanein, The Photomagneton in Quantum Field Theory (World Scientific, Singapore, 1994). 6. M. W. Evans and S. Kielich, eds., Modern Non-Linear Op ...
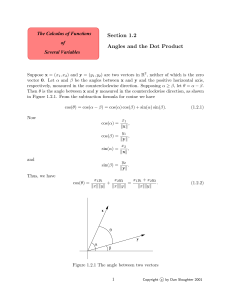
18.02SC Notes: Geometry of linear systems of equations
... the intersection of three planes, i.e., the point or points which lie on all three planes. Usually, three planes intersect in a point. You can visualize this by first imagining two of the planes intersecting in a line and then the line intersecting the third plane in a point. Altogether there are fou ...
... the intersection of three planes, i.e., the point or points which lie on all three planes. Usually, three planes intersect in a point. You can visualize this by first imagining two of the planes intersecting in a line and then the line intersecting the third plane in a point. Altogether there are fou ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.