New General Mathematics for Secondary Schools 3 Teacher`s Guide
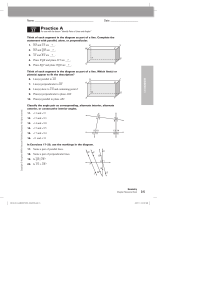
... 3. Interior opposite angles are not supplementary if lines are not parallel. ...
... 3. Interior opposite angles are not supplementary if lines are not parallel. ...
Chapter 2
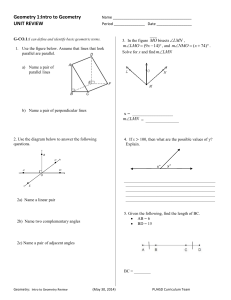
... One of the basic axioms of Euclidean geometry says that two points determine a unique line. ...
... One of the basic axioms of Euclidean geometry says that two points determine a unique line. ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.