Download Geometry Understand congruence and similarity using physical

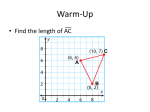
Connie Laughlin
Hank Kepner
Rosann Hollinger
Cynthia Schoonover
Kevin McLeod
Mary Mooney
1
We are learning to …
recognize and apply connections
across domains in the CCSSM.
2
We will know we are successful
when we can…
explain a specific example of
coherence across domains.
3
How can you
describe the
“lean” of the
Leaning Tower of
Pisa?
4
With a partner…
 Draw three new right triangles on the line.
Each should be a different size. Label each
triangle with as much information as you
can.
 What do these triangles have in common?
 What are some relationships among these
triangles?
5
Poster Presentations
What did we find?
6
The Teacher Perspective
What are the big ideas you would
like students to understand?
7
Apply
 What if I draw a right triangle for this line with
a horizontal change of 40? How big will the
vertical change be?
 What if I draw several right triangles on a
different line? Can I still use the same ratio to
find a missing vertical or horizontal change?
8
With your partner…
 Scan the Grade 8 Standards.
 Identify standards that appear to
relate to the lesson.
 Link two of the standards you
chose to highlight the
connections between them.
9
Grade 8
Equations and Expressions
Understand the connections between
proportional relationships, lines, and
linear equations.
6. Use similar triangles to explain
why the slope m is the same
between any two distinct points on
Geometry
Understand congruence and similarity
using physical models, transparencies,
or geometry software.
5. Use informal arguments
to establish…about the
a non-vertical line in the coordinate
angles created when parallel
plane…
lines are cut by a transversal.
10
The Logical Argument
 Parallel sides of the right triangles are parallel lines
crossing a transversal.
 Therefore, the parallel lines make congruent angles with
the traversals.
 Therefore, any two triangles are similar (AA~).
 Therefore, the ratios of corresponding sides are equal.
 This explains why the slope is the same between any two
distinct points on a non-vertical line in a coordinate
plane.
11
We are learning to recognize and
apply connections across domains in
the CCSSM.
We will be successful when we can
explain a specific example of
coherence across domains.
12
Making Connections
 What have I learned in this session?
 What will I share at my schools?
With whom/why? How?
13