Mechanics & Molecular Kinetic Theory
... speed (m/s) = distance (m) time(s) velocity (m/s) = displacement (m) time (s) acceleration (m/s2) = change in speed (m/s) time taken (s) ...
... speed (m/s) = distance (m) time(s) velocity (m/s) = displacement (m) time (s) acceleration (m/s2) = change in speed (m/s) time taken (s) ...
Ch. 6 Section 6.1 Powerpoint
... destroyed, but can be converted between forms. •The First Law of Thermodynamics: The total energy content of the universe is constant. ...
... destroyed, but can be converted between forms. •The First Law of Thermodynamics: The total energy content of the universe is constant. ...
CALCULUS
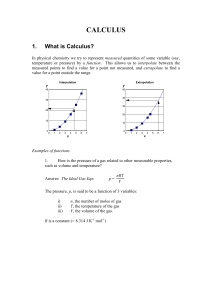
... but you should realise that in chemistry we are dealing with quantities in the real world, and so we try to give them meaningful symbols (p for pressure, V for volume, etc.), and you can usually tell which are variables because they are in italics.. Therefore we often get functions like A(r) = r2 F ...
... but you should realise that in chemistry we are dealing with quantities in the real world, and so we try to give them meaningful symbols (p for pressure, V for volume, etc.), and you can usually tell which are variables because they are in italics.. Therefore we often get functions like A(r) = r2 F ...
Blackbody radiation derivation of Planck`s
... – Electrons and ions of matter were treated as a simple harmonic oscillators (springs) subject to the driving force of applied E-M fields; matter becomes polarized by induction of electric dipoles • It models optical properties of materials and provides theory of refraction, reflectance and absorpti ...
... – Electrons and ions of matter were treated as a simple harmonic oscillators (springs) subject to the driving force of applied E-M fields; matter becomes polarized by induction of electric dipoles • It models optical properties of materials and provides theory of refraction, reflectance and absorpti ...
lecture2.pdf
... + ∇ · (ρv) = 0 ∂t 2. Momentum equations / Newton’s second law ∂(ρv) + ∇ · (ρv ⊗ v) = −∇p + ∇ · τ + ρg ∂t 3. Energy equation / first law of thermodynamics ...
... + ∇ · (ρv) = 0 ∂t 2. Momentum equations / Newton’s second law ∂(ρv) + ∇ · (ρv ⊗ v) = −∇p + ∇ · τ + ρg ∂t 3. Energy equation / first law of thermodynamics ...
Kinetics: Work, Energy and Power 193 8.6 Spatial (3D) Mechanical
... vertical), ½ m vz2 and ½ I wz2, respectively. Work done in the Z direction is similar to calculating work done along the other axes, that is, Wz = Fz sz. Thus, the total mechanical energy (E) of a rigid body is calculated as follows: ...
... vertical), ½ m vz2 and ½ I wz2, respectively. Work done in the Z direction is similar to calculating work done along the other axes, that is, Wz = Fz sz. Thus, the total mechanical energy (E) of a rigid body is calculated as follows: ...
Week 2
... A ball is dropped from a height of 20 m. You can use the relation between the work done by gravity and the change in the ball’s kinetic energy to determine the speed of the ball at any point in its free fall. The speed of the ball when it hits the ground = _____________ m/s. ...
... A ball is dropped from a height of 20 m. You can use the relation between the work done by gravity and the change in the ball’s kinetic energy to determine the speed of the ball at any point in its free fall. The speed of the ball when it hits the ground = _____________ m/s. ...
Document
... – Heat is positive if it flows into the system – Heat capacity, C: the amount of thermal energy that must be added to a system per unit temperature rise under specific conditions. dq C dt ...
... – Heat is positive if it flows into the system – Heat capacity, C: the amount of thermal energy that must be added to a system per unit temperature rise under specific conditions. dq C dt ...
Atomic Structure
... a. Internal energy is related to temperature. The human body has fairly constant temperature, hence the internal energy does not decrease as described above. b. Internal energy is added to the body to balance the continual decrease due to heat flow from the body and work being done by the body. The ...
... a. Internal energy is related to temperature. The human body has fairly constant temperature, hence the internal energy does not decrease as described above. b. Internal energy is added to the body to balance the continual decrease due to heat flow from the body and work being done by the body. The ...
Electrophilic Additions to Double Bonds
... electrons are too small and too light to be described by classical mechanics electrons need to be described by quantum mechanics accurate energy and potential energy surfaces for molecules can be calculated using modern electronic structure methods ...
... electrons are too small and too light to be described by classical mechanics electrons need to be described by quantum mechanics accurate energy and potential energy surfaces for molecules can be calculated using modern electronic structure methods ...
13.7 The Connection between Classical and Statistical
... • Fermions include particles such as electrons, positrons, protons, neutrons, etc. They all have halfinteger spin. • Fermions obey the Pauli exclusion principle, i.e. each quantum state can only accept one particle. • Therefore, for fermions Nj cannot be larger than gj. • FD statistic is useful in c ...
... • Fermions include particles such as electrons, positrons, protons, neutrons, etc. They all have halfinteger spin. • Fermions obey the Pauli exclusion principle, i.e. each quantum state can only accept one particle. • Therefore, for fermions Nj cannot be larger than gj. • FD statistic is useful in c ...
Summary presentation 10.2 File
... This equation is also valid if the gas is compressed. In the compression, work is done on the gas and the volume is decreased. Therefore, V is negative which means that W will be negative. From the first law of thermodynamics this means that positive work is done on the gas. ...
... This equation is also valid if the gas is compressed. In the compression, work is done on the gas and the volume is decreased. Therefore, V is negative which means that W will be negative. From the first law of thermodynamics this means that positive work is done on the gas. ...
Heat transfer physics

Heat transfer physics describes the kinetics of energy storage, transport, and transformation by principal energy carriers: phonons (lattice vibration waves), electrons, fluid particles, and photons. Heat is energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is also transformed (converted) among various carriers.The heat transfer processes (or kinetics) are governed by the rates at which various related physical phenomena occur, such as (for example) the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level (atom or molecule length scale) to macroscale are the laws of thermodynamics, including conservation of energy.