Download lecture2.pdf

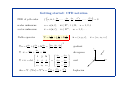
Getting started: CFD notation
∂u ∂u
∂2u
∂pu
∂u
,
.
.
.
,
,
,
,
.
.
.
,
∂x1
∂xn ∂t ∂x1 ∂x2
∂tp
PDE of p-th order
f u, x, t,
scalar unknowns
u = u(x, t),
vector unknowns
v = v(x, t),
Nabla operator
∂
∂
∂
∇ = i ∂x
+ j ∂y
+ k ∂z
∇u =
i ∂u
∂x
∇·v =
+
∂vx
∂x
j ∂u
∂y
+


∇ × v = det 

+
∂vy
∂y
i
∂
∂x
k ∂u
∂z
+
=
h
x ∈ Rn , t ∈ R,
v ∈ Rm ,
∂u ∂u ∂u
∂x , ∂y , ∂z
∂
∂y
k
∂
∂z
vx vy vz
∆u = ∇ · (∇u) = ∇2 u =
m = 1, 2, . . .
v = (vx , vy , vz )
gradient
z
∂vz
∂z
j
=0
n = 1, 2, 3
x = (x, y, z),
iT
v
divergence


 
=
 
∂2u
∂x2
+
∂vz
∂y
∂vx
∂z
∂vy
∂x
∂2u
∂y 2
−
−
−
+
∂vy
∂z
∂vz
∂x
∂vx
∂y
∂2u
∂z 2




k
curl
i
x
Laplacian
j
y
Tensorial quantities in fluid dynamics
Velocity gradient


∇v = [∇vx , ∇vy , ∇vz ] = 

∂vy
∂x
∂vy
∂y
∂vy
∂z
∂vx
∂x
∂vx
∂y
∂vx
∂z
∂vz
∂x
∂vz
∂y
∂vz
∂z
1111111111111111
0000000000000000
0000000000000000
1111111111111111




v
1111111111111111
0000000000000000
0000000000000000
1111111111111111
Remark. The trace (sum of diagonal elements) of ∇v equals ∇ · v.
Deformation rate tensor (symmetric part of ∇v)


1

T
D(v) = (∇v + ∇v ) = 
2

Spin tensor
1
2
1
2
S(v) = ∇v − D(v)
∂vx
∂x
∂vx
∂y
+
∂vx
∂z
+
∂vy
∂x +
∂vy
∂y
1 ∂vy
2
∂z +
1
2
∂vy
∂x
∂vz
∂x
∂vx
∂y
∂vz
∂y
1
2
1
2
(skew-symmetric part of ∇v)
∂vz
∂x
+
∂vz
∂y
+
∂vz
∂z





∂vx
∂z
∂vy
∂z
Vector multiplication rules
Scalar product of two vectors
a, b ∈ R3 ,




a · b = aT b = [a1 a2 a3 ] 
 b2  = a1 b1 + a2 b2 + a3 b3 ∈ R
b3
v · ∇u = vx
Example.
b1

∂u
∂u
∂u
+ vy
+ vz
∂x
∂y
∂z
convective derivative
Dyadic product of two vectors
3
a, b ∈ R ,



a1
a1 b1





a ⊗ b = abT = 
 a2  [b1 b2 b3 ] =  a2 b1
a3
a3 b1
a1 b2
a2 b2
a3 b2
a1 b3


3×3
a2 b3 
∈R
a3 b3
Elementary tensor calculus
T = {tij } ∈ R3×3 , α ∈ R
1.
αT = {αtij },
2.
T 1 , T 2 ∈ R3×3 , a ∈ R3
T 1 + T 2 = {t1ij + t2ij },


t t t
3
 11 12 13  P
ai [ti1 , ti2 , ti3 ]
a · T = [a1 , a2 , a3 ]  t21 t22 t23  =
| {z }
i=1
t31 t32 t33
i-th row
 
 

t
a
t t t
3
 1j 
 11 12 13   1  P
T · a =  t21 t22 t23   a2  =
 t2j  aj (j-th column)
j=1
t3j
a3
t31 t32 t33



2
2
2
1
1
1
3
t11 t12 t13
t11 t12 t13
P



t1ik t2kj
T 1 · T 2 =  t121 t122 t123   t221 t222 t223  =
k=1
t231 t232 t233
t131 t132 t133
3.
4.
5.
6.
1
2
1
2 T
T : T = tr (T · (T ) ) =
3
3 P
P
i=1 k=1
t1ik t2ik
Divergence theorem of Gauß
Let Ω ∈ R3 and n be the outward unit normal to the boundary Γ = Ω̄\Ω.
Then
Z
Ω
∇ · f dx =
Z
Γ
f · n ds
for any differentiable function f (x)
Example. A sphere: Ω = {x ∈ R3 : ||x|| < 1},
where
||x|| =
√
Consider f (x) = x
volume integral:
surface integral:
x·x=
p
so that
x2 + y 2 + z 2
Γ = {x ∈ R3 : ||x|| = 1}
is the Euclidean norm of x
∇ · f ≡ 3 in Ω
and n =
x
||x||
on Γ
4 3
∇ · f dx = 3
dx = 3|Ω| = 3 π1 = 4π
3
Ω
Ω
Z
Z
Z
Z
x·x
f · n ds =
ds =
||x|| ds =
ds = 4π
||x||
Γ
Γ
Γ
Γ
Z
Z
Governing equations of fluid dynamics
Physical principles
Mathematical equations
1. Mass is conserved
• continuity equation
2. Newton’s second law
• momentum equations
3. Energy is conserved
• energy equation
It is important to understand the meaning and significance of each equation
in order to develop a good numerical method and properly interpret the results
Description of fluid motion
z
v
Eulerian
monitor the flow characteristics
(x1 ; y1 ; z1 )
in a fixed control volume
i
Lagrangian
track individual fluid particles as
they move through the flow field
(x0 ; y0 ; z0 )
k
x
j
y
Description of fluid motion
Trajectory of a fluid particle
z
x = x(x0 , t)
v
(x1 ; y1 ; z1 )
(x0 ; y0 ; z0 )
k
i
j
y
x = x(x0 , y0 , z0 , t)
y = y(x0 , y0 , z0 , t)
z = z(x0 , y0 , z0 , t)
dx
= vx (x, y, z, t),
dt
dy
= vy (x, y, z, t),
dt
dz
= vz (x, y, z, t),
dt
x|t0 = x0
y|t0 = y0
z|t0 = z0
x
Definition. A streamline is a curve which is tangent to the velocity vector
v = (vx , vy , vz ) at every point. It is given by the relation
y
dx
dy
dz
=
=
vx
vy
vz
dy
dx
v
y(x)
=
vy
vx
x
Streamlines can be visualized by injecting tracer particles into the flow field.
Flow models and reference frames
Lagrangian
S
V
fixed CV of a finite size
dS
dV
fixed infinitesimal CV
V
integral
S
moving CV of a finite size
dS
dV
moving infinitesimal CV
Good news: all flow models lead to the same equations
differential
Eulerian
Eulerian vs. Lagrangian viewpoint
d
is the rate of change for a moving
Definition. Substantial time derivative dt
∂
fluid particle. Local time derivative ∂t
is the rate of change at a fixed point.
Let u = u(x, t), where x = x(x0 , t). The chain rule yields
∂u ∂u dx ∂u dy ∂u dz
∂u
du
=
+
+
+
=
+ v · ∇u
dt
∂t
∂x dt
∂y dt
∂z dt
∂t
substantial derivative = local derivative + convective derivative
Reynolds transport theorem
d
dt
Z
u(x, t) dV =
V ≡Vt
Vt
rate of change in
a moving volume
Z
=
∂u(x, t)
dV +
∂t
rate of change in
a fixed volume
Z
+
S≡St
u(x, t)v · n dS
convective transfer
through the surface
Derivation of the governing equations
Modeling philosophy
1. Choose a physical principle
• conservation of mass
• conservation of momentum
• conservation of energy
2. Apply it to a suitable flow model
• Eulerian/Lagrangian approach
• for a finite/infinitesimal CV
3. Extract integral relations or PDEs
which embody the physical principle
Generic conservation law
Z
Z
Z
∂
u dV +
f · n dS =
q dV
∂t V
S
V
S
f = vu − d∇u
n
V
dS
f
flux function
Divergence theorem yields
Z
Z
Z
∂u
dV +
∇ · f dV =
q dV
∂t
V
V
V
Partial differential equation
∂u
+∇·f =q
∂t
in V
Derivation of the continuity equation
Physical principle: conservation of mass
Z
Z
Z
d
∂ρ
dm
=
dV +
ρ dV =
ρv · n dS = 0
dt
dt Vt
∂t
S≡St
V ≡Vt
accumulation of mass inside CV = net influx through the surface
Divergence theorem yields
Z ∂ρ
+ ∇ · (ρv) dV = 0
∂t
V
Continuity equation
∂ρ
+ ∇ · (ρv) = 0
∂t
⇒
Lagrangian representation
∇ · (ρv) = v · ∇ρ + ρ∇ · v
Incompressible flows:
dρ
dt
=∇·v =0
⇒
dρ
+ ρ∇ · v = 0
dt
(constant density)
Conservation of momentum
Physical principle:
dV
dS
n
h
g
f = ma
(Newton’s second law)
total force
f = ρg dV + h dS,
body forces
g
gravitational, electromagnetic,. . .
surface forces
h
pressure + viscous stress
Stress tensor
σ = −pI + τ
where
h=σ·n
momentum flux
For a newtonian fluid viscous stress is proportional to velocity gradients:
τ = (λ∇ · v)I + 2µD(v),
where
τxx =
τyy =
τzz =
1
(∇v + ∇vT ),
2
2
λ≈− µ
3
Shear stress: deformation
Normal stress: stretching
x
λ∇ · v + 2µ ∂v
∂x
∂v
λ∇ · v + 2µ ∂yy
z
λ∇ · v + 2µ ∂v
∂z
D(v) =
τxy = τyx = µ
y
xx
τxz = τzx
τyz = τzy
x
“
∂vy
∂x
+
∂vx
∂y
”
` x
´
∂vz
= µ ∂v
+
∂x ”
“ ∂z
∂v
z
+ ∂zy
= µ ∂v
∂y
y
yx
x
Derivation of the momentum equations
Newton’s law for a moving volume
Z
Z
Z
d
∂(ρv)
ρv dV =
dV +
(ρv ⊗ v) · n dS
dt Vt
∂t
V ≡Vt
S≡St
Z
Z
=
ρg dV +
σ · n dS
V ≡Vt
S≡St
Transformation of surface integrals
Z
Z ∂(ρv)
+ ∇ · (ρv ⊗ v) dV =
[∇ · σ + ρg] dV,
∂t
V
V
σ = −pI + τ
∂(ρv)
+ ∇ · (ρv ⊗ v) = −∇p + ∇ · τ + ρg
∂t
∂(ρv)
∂v
∂ρ
dv
+ ∇ · (ρv ⊗ v) = ρ
+ v · ∇v + v
+ ∇ · (ρv) = ρ
∂t
∂t
∂t
dt
|
|
{z
}
{z
}
Momentum equations
substantial derivative
continuity equation
Conservation of energy
Physical principle:
dV
dS
n
h
g
δe = s + w
(first law of thermodynamics)
δe
accumulation of internal energy
s
heat transmitted to the fluid particle
w
rate of work done by external forces
Heating: s = ρq dV − fq dS
q
internal heat sources
fq
diffusive heat transfer
T
κ
absolute temperature
thermal conductivity
Work done per unit time =
Fourier’s law of heat conduction
fq = −κ∇T
the heat flux is proportional to the
local temperature gradient
total force × velocity
w = f · v = ρg · v dV + v · (σ · n) dS,
σ = −pI + τ
Derivation of the energy equation
Total energy per unit mass:
|v|2
2
specific internal energy due to random molecular motion
e
|v|
2
E =e+
2
specific kinetic energy due to translational motion
Integral conservation law for a moving volume
Z
Z
Z
∂(ρE)
d
ρE dV =
ρE v · n dS
dV +
dt Vt
∂t
V ≡Vt
S≡St
Z
Z
=
ρq dV +
κ∇T · n dS
V ≡Vt
S≡St
Z
Z
v · (σ · n) dS
ρg · v dV +
+
V ≡Vt
accumulation
heating
work done
S≡St
Transformation of surface integrals
Z Z
∂(ρE)
+ ∇ · (ρEv) dV =
[∇ · (κ∇T ) + ρq + ∇ · (σ · v) + ρg · v] dV,
∂t
V
V
where ∇ · (σ · v) = −∇ · (pv) + ∇ · (τ · v) = −∇ · (pv) + v · (∇ · τ ) + ∇v : τ
Different forms of the energy equation
Total energy equation
∂(ρE)
+ ∇ · (ρEv) = ∇ · (κ∇T ) + ρq − ∇ · (pv) + v · (∇ · τ ) + ∇v : τ + ρg · v
∂t
∂ρ
dE
∂(ρE)
∂E
+ ∇ · (ρEv) = ρ
+ v · ∇E + E
+ ∇ · (ρv) = ρ
∂t
∂t
∂t
dt
{z
}
{z
}
|
|
substantial derivative
Momentum equations
ρ
ρ
dv
= −∇p + ∇ · τ + ρg
dt
continuity equation
(Lagrangian form)
dE
de
dv
∂(ρe)
=ρ +v·ρ
=
+ ∇ · (ρev) + v · [−∇p + ∇ · τ + ρg]
dt
dt
dt
∂t
Internal energy equation
∂(ρe)
+ ∇ · (ρev) = ∇ · (κ∇T ) + ρq − p∇ · v + ∇v : τ
∂t
Summary of the governing equations
1. Continuity equation / conservation of mass
∂ρ
+ ∇ · (ρv) = 0
∂t
2. Momentum equations / Newton’s second law
∂(ρv)
+ ∇ · (ρv ⊗ v) = −∇p + ∇ · τ + ρg
∂t
3. Energy equation / first law of thermodynamics
∂(ρE)
+ ∇ · (ρEv) = ∇ · (κ∇T ) + ρq − ∇ · (pv) + v · (∇ · τ ) + ∇v : τ + ρg · v
∂t
|v|2
E =e+
,
2
∂(ρe)
+ ∇ · (ρev) = ∇ · (κ∇T ) + ρq − p∇ · v + ∇v : τ
∂t
This PDE system is referred to as the compressible Navier-Stokes equations
Conservation form of the governing equations
Generic conservation law for a scalar quantity
∂u
+ ∇ · f = q,
∂t
where
f = f (u, x, t)
Conservative variables, fluxes and sources



ρv
ρ





U =
ρv ⊗ v + pI − τ
 ρv  , F = 
(ρE + p)v − κ∇T − τ · v
ρE
is the flux function


,



Q=

0
ρg
ρ(q + g · v)




Navier-Stokes equations in divergence form
∂U
+∇·F=Q
∂t
U ∈ R5 ,
F ∈ R3×5 ,
Q ∈ R5
• representing all equations in the same generic form simplifies the programming
• it suffices to develop discretization techniques for the generic conservation law
Constitutive relations
Variables:
ρ, v, e, p, τ , T
Equations: continuity, momentum, energy
The number of unknowns exceeds the number of equations.
1. Newtonian stress tensor
τ = (λ∇ · v)I + 2µD(v),
D(v) =
1
(∇v + ∇vT ),
2
2
λ≈− µ
3
2. Thermodynamic relations, e.g.
p = ρRT
ideal gas law
R
specific gas constant
e = cv T
caloric equation of state
cv
specific heat at constant volume
Now the system is closed: it contains five PDEs for five independent variables
ρ, v, e and algebraic formulae for the computation of p, τ and T . It remains to
specify appropriate initial and boundary conditions.
Initial and boundary conditions
Initial conditions
ρ|t=0 = ρ0 (x),
v|t=0 = v0 (x),
e|t=0 = e0 (x)
Let Γ = Γin ∪ Γw ∪ Γout
Boundary conditions
w
Γin = {x ∈ Γ : v · n < 0}
Inlet
ρ = ρin ,
v = vin ,
in Ω
e = ein
in
out
prescribed density, energy and velocity
w
Solid wall
Γw = {x ∈ Γ : v · n = 0}
Outlet
Γout = {x ∈ Γ : v · n > 0}
v · n = vn
or
v=0
no-slip condition
T = Tw
fq
∂T
∂n = − κ
given temperature or
v · s = vs
prescribed heat flux
prescribed velocity
or
−p + n · τ · n = 0
s·τ ·n=0
vanishing stress
The problem is well-posed if the solution exists, is unique and depends continuously
on IC and BC. Insufficient or incorrect IC/BC may lead to wrong results (if any).