from last time:
... often done by educated guessing, and there may be more than one solution. Apply boundary conditions – these will often limit your values of energy. Evaluate any undetermined constants (like amplitudes), e.g. by using boundary conditions, applying normalisation. Check your solution, if it gives you s ...
... often done by educated guessing, and there may be more than one solution. Apply boundary conditions – these will often limit your values of energy. Evaluate any undetermined constants (like amplitudes), e.g. by using boundary conditions, applying normalisation. Check your solution, if it gives you s ...
Introduction to Quantum Mechanics: Homework #1 (Due by Sep
... 4) If all the photoelecrtrons are collected, what is the current in ampere (A)? 5) Calculate the maximum wavelength of a UV light with which you can observe the photoelectric effect from the Ni sample. 9. Based on the Bohr model of a H atom, 1) Show that the Bohr radius (the radius of the smallest o ...
... 4) If all the photoelecrtrons are collected, what is the current in ampere (A)? 5) Calculate the maximum wavelength of a UV light with which you can observe the photoelectric effect from the Ni sample. 9. Based on the Bohr model of a H atom, 1) Show that the Bohr radius (the radius of the smallest o ...
CH7 handout is here.
... 8. Heisenberg uncertainty principle states that we cannot know exactly the position and velocity of an electron both at the same instant. Explain what we studied under ‘position’ and under ‘velocity’. What were the assumptions when studying ‘position’? “velocity”? ...
... 8. Heisenberg uncertainty principle states that we cannot know exactly the position and velocity of an electron both at the same instant. Explain what we studied under ‘position’ and under ‘velocity’. What were the assumptions when studying ‘position’? “velocity”? ...
Slide 1
... Nanocrystals are zero dimensional nanomaterials, which exhibit strong quantum confinement in all three dimensions, and thus they are also called “quantum dots”. ...
... Nanocrystals are zero dimensional nanomaterials, which exhibit strong quantum confinement in all three dimensions, and thus they are also called “quantum dots”. ...
Lecture 14
... variables are the spherical coordinates r,θ,φ. Today we draw the conclusions from these considerations. Wavefunctions of the stationary states The fact that there are three dimensions means that there are also three quantum numbers: n = ‘the principal quantum number’, associated with R(r) l = ‘the a ...
... variables are the spherical coordinates r,θ,φ. Today we draw the conclusions from these considerations. Wavefunctions of the stationary states The fact that there are three dimensions means that there are also three quantum numbers: n = ‘the principal quantum number’, associated with R(r) l = ‘the a ...
Physics 125a – Problem Set 5 – Due Nov 12,... Version 3 – Nov 11, 2007
... (a) Consider a potential of the form V (x) = −a V0 δ(x). Show that it admits a bound state m a2 V 2 of energy E = − 2 ~2 0 . Are there any other bound states? (b) Calculate the free states and reflection and transmission probabilities as functions of energy using the probability current. Hint: Solve ...
... (a) Consider a potential of the form V (x) = −a V0 δ(x). Show that it admits a bound state m a2 V 2 of energy E = − 2 ~2 0 . Are there any other bound states? (b) Calculate the free states and reflection and transmission probabilities as functions of energy using the probability current. Hint: Solve ...
HWU4-21 QUESTION: The principal quantum number, n, describes
... The principal quantum number, n, describes the energy level of a particular orbital as a function of the distance from the center of the nucleus. Additional quantum numbers exist to quantify the other characteristics of the electron. The angular momentum quantum number (ℓ), the magnetic quantum numb ...
... The principal quantum number, n, describes the energy level of a particular orbital as a function of the distance from the center of the nucleus. Additional quantum numbers exist to quantify the other characteristics of the electron. The angular momentum quantum number (ℓ), the magnetic quantum numb ...
Postulate 1 of Quantum Mechanics (wave function)
... a finite range), and normalized (the probability of find it somewhere is 1). ...
... a finite range), and normalized (the probability of find it somewhere is 1). ...
Quantum Mechanics
... a real possibility that you do not know where it actually is This is typically a very small number (10-30) for ordinary objects, but for electrons and other tiny objects it is on the order at which they exist ...
... a real possibility that you do not know where it actually is This is typically a very small number (10-30) for ordinary objects, but for electrons and other tiny objects it is on the order at which they exist ...
Modern physics 2330
... 13- ( ) The Heisenberg uncertainty principle states that, position and conjugate momentum can not be measured simultaneously with any degree of accuracy. 14- ( ) A wave packet is a superposition of many plane waves. 15- ( ) Double slit experiment shows that it is impossible to measure both the parti ...
... 13- ( ) The Heisenberg uncertainty principle states that, position and conjugate momentum can not be measured simultaneously with any degree of accuracy. 14- ( ) A wave packet is a superposition of many plane waves. 15- ( ) Double slit experiment shows that it is impossible to measure both the parti ...
Quantum Mechanical Energy and You!
... quantities that are highly non local and spread through space in time. Thus, the idea of how we talk of the fundamental quantity position must be re-invented, as well as all secondary quantities. ...
... quantities that are highly non local and spread through space in time. Thus, the idea of how we talk of the fundamental quantity position must be re-invented, as well as all secondary quantities. ...
Chemistry 1 Concept 5 “Electrons in Atoms” Study Guide
... 17. The quantum number that indicates the position of an orbital about the three axes in space is the ___________________________________ 18. The spin quantum number indicates that the number of possible spin states for an electron in an orbital is __________ 19. The angular momentum quantum number ...
... 17. The quantum number that indicates the position of an orbital about the three axes in space is the ___________________________________ 18. The spin quantum number indicates that the number of possible spin states for an electron in an orbital is __________ 19. The angular momentum quantum number ...
quantum1
... •Describes the time evolution of your wavefunction. •Takes the place of Newton’s laws and conserves energy of the system. •Since “particles” aren’t particles but wavicles, it won’t give us a precise position of an individual particle, but due to the statistical nature of things, it will precisely de ...
... •Describes the time evolution of your wavefunction. •Takes the place of Newton’s laws and conserves energy of the system. •Since “particles” aren’t particles but wavicles, it won’t give us a precise position of an individual particle, but due to the statistical nature of things, it will precisely de ...
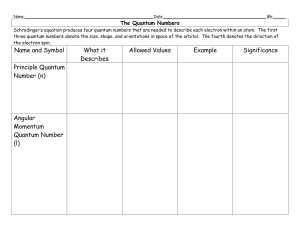
e-the-quantum-numberssv-2
... The Quantum Numbers Schrodinger’s equation produces four quantum numbers that are needed to describe each electron within an atom. The first three quantum numbers denote the size, shape, and orientations in space of the orbital. The fourth denotes the direction of the electron spin. ...
... The Quantum Numbers Schrodinger’s equation produces four quantum numbers that are needed to describe each electron within an atom. The first three quantum numbers denote the size, shape, and orientations in space of the orbital. The fourth denotes the direction of the electron spin. ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.