* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Exam 1 - RIT
Laplace–Runge–Lenz vector wikipedia , lookup
Classical mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Center of mass wikipedia , lookup
Coriolis force wikipedia , lookup
Jerk (physics) wikipedia , lookup
Accretion disk wikipedia , lookup
Equations of motion wikipedia , lookup
Centrifugal force wikipedia , lookup
Fictitious force wikipedia , lookup
Earth's rotation wikipedia , lookup
Seismometer wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Mass versus weight wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Rigid body dynamics wikipedia , lookup
147028615
Name_ _____________________
Exam 3
Thursday, 8 May 2008
Page 1 of 23
******BE SURE TO SCROLL ALL THE WAY TO END!!!
Formula sheet will be provided … see below…
Bring ruler with millimeter markings
Bring a protractor (unlikely, but just in case)
Bring a fully charged calculator
******BE SURE TO SCROLL ALL THE WAY TO END!!!
6/25/2017
147028615
Name_ _____________________
Page 2 of 23
Descriptions of some of the topics covered
Unit conversion (Conversion relations will be given)
Scientific notation
Significant figures and rules for arithmetic operations
Measurement uncertainty
Proper form
NEW STUFF: Circular motion – Mainly Chapters 6 and 7; a small
amount of stuff from Chapters 8 and 9.
Uniform circular motion
Non uniform circular motion
Torque, moment of inertia, Newton’s 2nd Law for rotation
Some angular momentum
6/25/2017
147028615
Name_ _____________________
Page 3 of 23
Formula sheet (preliminary)
Unit Systems
Length Mass Time Force
SI / MKS
m
kg
s
N
CGS
cm
g
s
dyne
BE
ft
slug s
lb
Significant figures
In Dr. Entenberg’s class, trailing zeroes will be meaningful unless the number has quotes around it, i.e. “75,000” nails.
Use a decimal point when you know the correct number of significant figures.
Whole numbers have no decimal point; e.g., 3 = 3.0000000…….
If unsure, use scientific notation to determine the number of significant figures.
Proper form: [(A + A) 10exponent units] where A must be written to 1 significant figure
Note that A and A must have
1. Common exponent outside the parentheses
2. Common units outside the parentheses
3. Same number of decimal places inside the parentheses
Scientific notation example: 3769. m = 3.769 X 103 m
Uncertainty propagation examples:
f=X*Y
f = fmax – f where fmax = (X + X) * (Y + Y)
f=X/Y
f = fmax – f where fmax = (X + X) / (Y – Y)
Constants
Geometry
Trigonometry
g = 9.80 m/s2 g = 980. cm/s2 g = 32.2 ft/s2 G = 6.67 x 10-11 N m2 / kg2
2 R R2 4 R2 (4/3) R3 R2 H
sine = opp / hyp
cosine = adj / hyp tangent = opp / adj = sine/cosine
Vectors in 2-D
Vectors in 2-D
Vectors in 2-D
Symbol
F = |F| = magnitude ( + ONLY)
Fx = component along x direction ( + )
Fx= + F cos (or Fx= + F sin ’)
= angle wrt a given direction ( + )
Fy = component along y direction ( + )
Fy= + F sin (or Fy= + F cos ’)
Force and Vector NOTATION:
Fnet F F1 F2 F3 F4 =
6/25/2017
Fnet = F = F1 + F2 + F3 + F4….
147028615
Name_ _____________________
Page 4 of 23
Variables, definitions, and equations
Angular variables
Rigid body rotation
“moment of inertia” angular mass
I = mrperp2 (see below for more info)
Tangential variables
Point P on rigid body
Mass
Linear variables
X and Y motions
“linear mass”
m or M
Position
Displacement
Average velocity
Average acceleration
Linear variables
X
X = Xfinal – Xinitial
vxavg = x / t
axavg = vx / t
Angular variables
= final – initial
avg = t
avg = t
Tangential variables
Stan = + r
Constant acceleration equations
Velocity time equation
Position time equation
Velocity position equation
aX = (aX)avg = constant
Vxf = Vxi + ax t
Xf = Vxi t + ½ ax t2
Vxf 2 = Vxi 2 + 2 ax X
= avg = constant
f t
fi t + ½ t2
f 2 = i 2 + 2
Force: Newton’s 2nd Law
Torque: Newton’s 2nd Law
Fx = M ax
Various Force Magnitudes
Gravitational force (general)
Grav force at earth’s surface
Friction force magnitude
Normal force magnitude
Tension force magnitude
= I
Center of mass (center of gravity)
Vtan = + r
atan = + r
= + r F
+CCL , -CL
= + r F sin()
F = G M1 M2 / r2
G = 6.67 x 10-11 N m2 / kg2
Wt = M g where g = [G ME / RE2] = 9.80 m/s2
fs < fsmax fsmax =s Fn fkin = k Fn
Fn or n
Ft or T
Two dimensional circular motion: Centripetal (radial) acceleration = ar = V2 / r = 2 r
{Newton’s Universal Law of Gravitation}
Tangential acceleration = at = r
Xcg = (M1 X1 + M2 X2 + … + MN XN) / (M1 + M2 + … + MN)
Moment of inertia: point mass (m r2), hoop (M R2), solid disk (½ M R2), sphere [(2/5) M R2 ], rod, at end [(1/3) M L2 ]
6/25/2017
147028615
Name_ _____________________
Page 5 of 23
A PROBLEM THAT SHOULD HAVE BEEN ON EXAM 2
Vector 1
Box B
Vector
2
Vector 3
Vector 4
Earth E
In the above figure, a box is sitting on top of the earth. Four equal magnitude force vectors 1, 2, 3, and 4 are shown.
_______ Vector 1 represents
(a) the normal force on the box by the earth
(b) the normal force on the earth by the box
(c) the gravitational force on the box by the earth
(d) the gravitational force on the earth by the box
_______ Vector 2 represents
(a) the normal force on the box by the earth
(b) the normal force on the earth by the box
(c) the gravitational force on the box by the earth
(d) the gravitational force on the earth by the box
_______ Vector 3 represents
(a) the normal force on the box by the earth
(b) the normal force on the earth by the box
(c) the gravitational force on the box by the earth
(d) the gravitational force on the earth by the box
6/25/2017
147028615
Name_ _____________________
Page 6 of 23
_______ Vector 4 represents
(a) the normal force on the box by the earth
(b) the normal force on the earth by the box
(c) the gravitational force on the box by the earth
(d) the gravitational force on the earth by the box
_______ The “action and reaction” pairs are
(a) Vectors 1 and 2, Vectors 3 and 4
(b) Vectors 1 and 3, Vectors 2 and 4
(c) Vectors 1 and 4, Vectors 2 and 3
(d) None of these
_______ The following vector pair consists only of “contact” forces
(a) Vectors 1 and 2 (b) Vectors 3 and 4 (c) Vectors 1 and 3 (d) Vectors 2 and 4
_______ The following vector pair consists only of “action at a distance” forces
(a) Vectors 1 and 2 (b) Vectors 3 and 4 (c) Vectors 1 and 3 (d) Vectors 2 and 4
6/25/2017
147028615
Name_ _____________________
Page 7 of 23
_______ The SI torque unit is equivalent to
(a) N s
(b) N kg
(c) kg m2 / s2
(d) kg m / s2
_______ The SI angular unit is called the
(a) degree
(b) radian
(c) arc second
(d) radian meter
_______ The SI angular unit is equivalent to
(a) 180°
(b) 57.3°
(c) 60°
(e) 114.6°_______
A car moves in a circle of radius (854.23 + 0.06) m with period for one rotation of (17.03 + .09) s.
(a) Determine the speed V of the car. Use the usual rules for significant figures.
(b) Determine the uncertainty V = (Vmax – V) in the speed and then write it to one significant figure.
(c) Write the speed of the car in proper form.
(d) Compare the significant figures for the speed in part (a) to the significant figures for the speed in part (c). Are the significant
figures the same?
A (300.3 0.4) kg object moves clockwise around a horizontal circle of radius (52.8 0.3) m with a
constant speed of (711.06 0.04) m/s.
(a)
On the diagram to the right, sketch and label the net force Fnet on the object while at the
point indicated by the dot.
(b)
If the object were moving counterclockwise around the circle, would the direction of the net
force change? If so, in what direction would it then point?
(c)
mv2
, determine the magnitude of the net force Fnet
Using the expression for the net force Fnet
r
and its uncertainty. Write the result in “proper form” (units, power of ten, significant figures).
6/25/2017
147028615
Name_ _____________________
Page 8 of 23
II C. A car moves counterclockwise at constant speed around the “peanut” shaped track shown. The track contains two
straight portions.
a) Draw velocity vectors at the points indicated with dots. Use long arrows where the magnitude of the velocity is large, short
arrows where it is small. Write “v = 0” if the velocity is zero.
b) Draw acceleration vectors at the points indicated with dots. Use long arrows where the magnitude of the acceleration is
large, short arrows where it is small. Write “a = 0” if the acceleration is zero.
6/25/2017
147028615
Name_ _____________________
Page 9 of 23
Construction of V = V2 – V1
V2
V1
On a flat surface, you run in a circle of radius 7.00 meters. You move in uniform circular motion with a period (for one
revolution) of 6.00 seconds. Your mass is 78.0 kg. At time t1, the velocity is V1 and at time t2, the velocity is V2.
(a) In the box above, carefully construct and label the change in the velocity V = V2 – V1 vector below.
Hint: V = V2 + ( – V1 )
(b) On the diagram at the top, sketch and label the acceleration vectors a1 and a2 of your body at the times t1 and t2.
(c) On the diagram at the top, sketch and label the force vectors F1 and F2 on you at the times t1 and t2.
(d) Calculate the speed V = | V1| = | V2| of the ball.
(e) Calculate the magnitude of the centripetal force on you.
(f) When you run with constant speed in a circle, explain why you have to lean toward the center of the circle. Hint: recall
discussion in class.
A clear diagram will improve your answer.
Discuss the “physical nature” is of the “centripetal force” that enables you to run in a circle.
Use back of page for more room.
6/25/2017
147028615
Name_ _____________________
Page 10 of 23
_______ You twirl a ball on a string in a circle. Ignoring the effect of gravity, the force that causes the ball to move in a circle is
(a) the tension force on the ball by the string
(b) the tension force on the string by the ball
(c) the tension force on the string by your hand
(d) the tension force on your hand by the string
_______ You run (without sliding) in a circle around a track. The force that causes you to move in a circle is
(a) the force of kinetic friction on your shoe by the track surface
(b) the force of kinetic friction on the track surface by your shoe
(c) the force of static friction on your shoe by the track surface
(d) the force of static friction on the track surface by your shoe
_______ You run (without sliding) in a circle around a track. The reason you must lean inward towards the center of the circle is to
(a) push inward on the track so that the track pushes outward on you
(b) push outward on the track so that the track pushes inward on you
(c) decrease your normal force to facilitate circular motion
(d) decrease your apparent weight to facilitate circular motion
6/25/2017
(4 pts) When you run with constant speed in a circle, explain why you have to
lean toward the center of the circle. Hint: recall discussion in class.
147028615
Name_ _____________________
Page 11 of 23
Example 6.5 (Figure 6.13) Finding the maximum
speed to turn a corner
What is the maximum speed with which a 1500. kg
car can make a turn around a curve of radius 20.0
m on a level (un-banked) road without sliding?
Assume that the coefficient of static friction for
rubber tires on pavement is s = 1.00 (see Table
5.1).
Answer 14. m/s.
Start by making free body diagrams for the top
view and the side view of car.
6/25/2017
147028615
Name_ _____________________
Page 12 of 23
A satellite, mass M, has a circular orbit about the Earth, mass ME and radius RE. The height of the satellite is H above sea level.
The force that causes the satellite to move in a circle is
(a) M g
(b) M G ME / RE2
(c) M G ME / (RE + H)2
(d) M g ME / (RE + H)2
_______ The true weight of an object, mass M, at rest on the Moon, mass M M and radius RM, is
(a) M g
(b) M G ME / RE2
(c) M G MM / RM2
(d) M g MM / RM2
On the diagram, the Moon (black dot) moves clockwise in uniform circular motion around the Earth. The average (center to
center) distance of the Moon from the Earth is 3.85 x 108 meters. The mass of the Earth is 5.98 x 1024 kg and the mass of the
Moon is 7.35 x 1022 kg.
(a) Use the black dot to the right to make a free body diagram of the moon at the same instant it is shown in the diagram. Label all
forces on the Moon.
(b) On the diagram, sketch and label the acceleration of the Moon.
(c) On the diagram, sketch and label the tangential velocity of the Moon.
(d) Calculate the centripetal force on the Moon.
You are given the Earth with its mass of 5.98 x 1024 kg and its radius of 6.37 x 106 m.
(a)
Use the standard method to calculate the weight of a 70.0 kg person standing on the Earth’s surface. Use SI units and 3 sig
figs.
(b)
Use Newton’s Law of Universal Gravitation to calculate the weight of the same 70.0 kg person. Start by making a
cartoon sketch of the person standing on the surface of the earth; sketch and label the radius of the Earth on your drawing.
6/25/2017
147028615
Name_ _____________________
Page 13 of 23
On the diagram, the Moon (black dot) moves clockwise in uniform circular motion around the Earth. The average (center to
center) distance of the Moon from the Earth is 3.85 x 108 meters. The mass of the Earth is 5.98 x 1024 kg and the mass of the
Moon is 7.35 x 1022 kg.
(a) (4 pts) Sketch and label the force on the Moon and the acceleration of the Moon. Also, sketch and label the tangential
velocity of the Moon. G = 6.67 x 10-11 N m2 / kg2
(b) (4 pts) What is the magnitude of the force on the Moon by the Earth?
(c) (4 pts) What is the tangential speed of the Moon in its approximately circular orbit about the Earth?
(d) (4 pts) What is the period or time that it takes the Moon to make a single revolution around the Earth? Give answer in Earth
days.
Is this what you expect? Look up the actual period of the Moon. Compare the two and calculate the % difference.
6/25/2017
147028615
Name_ _____________________
Uniform Circular Motion
M
V
Page 14 of 23
is motion in a circle with constant speed.
V=2r/T =
Constant speed of mass
M
r
T = period of the circular
motion
T = 24 hours = 86,400 s
for a geosynchronous
satellite
Explain in your own words what is meant by the term “geosynchronous” satellite.
Mention what is “special” about such a satellite.
V
MEarth = 5.98 x 1024 kg
r
REarth = 6.37 x 106 m
RE
H
On the figure, sketch and label the force on the satellite; also, sketch and label the
acceleration of the satellite.
6/25/2017
147028615
Name_ _____________________
Page 15 of 23
Use Newton’s law of universal gravitation, F = G MEarth MSat / r2 and Newton’s 2nd Law
(for centripetal force magnitude) FC = M aC to find the speed V necessary for the
satellite to stay in a circular orbit is V = ( G ME Msat / r )½. Note aC = |aC| = V2 / r Show
algebra below.
Use the relation V = 2 r / T and the above expression for V to derive Kepler’s 3rd Law
T2 = (4 G ME )) r3
Show algebra below
Use the period of the satellite to calculate the radius of the geosynchronous orbit. (4.23
X 107 m) Show setup for calculation clearly.
Find the height H above the earth’s surface. (3.59 X 107 m or “22,300” miles)
Show setup for calculation clearly.
Find the speed of the satellite. (3.08 X 103 m/s)
Show setup for calculation clearly.
6/25/2017
147028615
Name_ _____________________
Page 16 of 23
Given a compact disk at rest. The disk requires 2.50 s to reach a speed of 375.0 clockwise revolutions per minute. The
radius of the disk is 0.0575 m.
(a)
In SI units, calculate the final angular velocity of the compact disk.
(b) What is the tangential velocity of the black dot on the edge of the disk?
o At time t = 0, a tire has an angular velocity of 115.0 clockwise revolutions per minute. After 2.50 s, the angular velocity of the tire
is 375.0 clockwise revolutions per minute. The outer radius of the tire is 0.575 m.
(a) (3 pts) Write the angular velocity of the tire, after 2.50 s, in SI units.
Be sure to specify the correct sign!
(b) (2 pts) What is the tangential velocity of the black dot at the outer edge of the tire after 2.50 s?
(c) (3 pts) Determine the constant angular acceleration of the tire?
(d) (4 pts) How many revolutions does the black dot make after 2.50 s?
6/25/2017
147028615
Name_ _____________________
Y’ axis
Y axis
7.00 kg
3.00 kg
2.50 m
Page 17 of 23
X axis
2.50 m
The above dumbbell is a bar (negligible mass) of length 5.00 m with a small “point masses” of 3.00 kg on the left end and
7.00 kg on the right end. The origin is at the 7.00 kg mass.
_______ The X position of the center of gravity of the dumbbell is at
(a) the origin
(b) + 1.50 m
(c) – 1.50 m
(d) – 2.50 m
_______ The moment of inertia of the dumbbell about the Y axis of rotation is
(a) 75.0 kg m2
(b) 175. kg m2
(c) 250. kg m2
(d) 62.5. kg m2
_______ The moment of inertia of the dumbbell about the Y’ axis of rotation is
(a) 75.0 kg m2
(b) 175. kg m2
(c) 250. kg m2
(d) 62.5. kg m2
6/25/2017
147028615
Name_ _____________________
Page 18 of 23
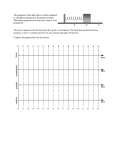
A mass m hangs by a string wrapped around a pulley of radius Rp 2.60 cm. The pulley is attached to a solid circular disk of
radius Rd 4.61 cm. The moment of inertia of the disk/pulley combination is 1.40 x 10-4 kg·m2. Assume the disk/pulley rotates
without friction. Assume the pulley has negligible mass. The angular velocity versus time graph of the disk/pulley is show in the
graph below.
Angular Velocity (rad/s)
Rd
200
Rp
150
100
50
m
0.2
0.4
0.6
0.8 1.0 Time (s)
(a) What is the net torque on the sysem?
(b) What is the tension in the string?
(c) What is the acceleration component ay of the small mass m? (Give correct sign.)
(d) What is the value of the hanging mass m?
(e) How fast will the small mass be going at time t = 0.800 s? You can do the problem using either Vt = r or Vyf = Vyi + ay t or
both formulas. You may also need at = r .
(f) What is the mass M of the large disk?
6/25/2017
147028615
Name_ _____________________
Page 19 of 23
y-axis
x-axis
m
A mass m hangs by a string wrapped around a small inner pulley of radius rP = 0.0800 m. The pulley is mounted on a solid
cylindrical disk of radius Rd = 0.280 m and mass Md. The moment of inertia of the disk plus the pulley is 1.40 kg m2. Assume
the disk/pulley rotates without friction. The mass m starts from rest and accelerates downward.
(b) The tension in the string is 650.0 N. Calculate the torque on the disk/pulley system.
Sketch and label the radial distance r and the force F┴ on the above figure.
(b) Calculate the angular acceleration of the system.
(c) Calculate the angular velocity of the disk/pulley after 5.00 seconds have elapsed.
(d) Assuming that the mass of the pulley is negligible, estimate the mass of the disk, Md? Hint: find the moment of inertia first by
getting the ratio of torque to angular acceleration.
6/25/2017
147028615
Name_ _____________________
Page 20 of 23
Example 7.8 The engine in a small plane is specified to have a torque of
500. Nm. This engine drives a 2.00 m long, 40.0 kg single blade propeller.
(a) What is the angular acceleration of the propeller? (37.5 rad/s2)
(b) On startup, how long does it take the propeller to reach 2000. rpm? (5.6 s)
6/25/2017
147028615
Name_ _____________________
Page 21 of 23
20.0º
Ft
40.0º
Given a fishing pole of length 3.00 m and inclined at an angle of 40.0 degrees with respect to the positive x-direction. The
tension (Ft = T) in the fishing line (at an angle of 20.0 degrees as shown) is 170. N. Calculate the torque on the pole about
the point where it is being held. Sketch and label the “perpendicular” component of the force.
Given a big wrench and a big nut that needs to be tightened on a big bolt. At a distance of 2 m from the center of the bolt, you
apply a force of 95 N to the wrench at the angle of 55˚ shown below.
(a) Label the axis of rotation (aor).
(c) Sketch and label the line of action (loa) on the diagram.
(d) Sketch and label the moment arm ( r┴ ) on the diagram.
(e) Calculate the torque that you are applying to the system. Be sure to specify the correct sign and the correct units.
55 ˚
2
m
6/25/2017
95 N
147028615
Name_ _____________________
Page 22 of 23
3.50 m
#1
#2
A uniform 20.0 kg board of length 6.00 m rests horizontally on two sawhorses as shown.
Place the “pivot point” or “axis of rotation” at the tip of sawhorse #2.
(a) Sketch all forces which act on the board at the location where each force acts.
(b) What is the torque (with the correct sign) due to the full weight of the board?
(c) The normal force magnitude from sawhorse #1 is 28.0 N. What is the torque due to the normal force from sawhorse #1 with the
correct sign?
6/25/2017
147028615
Name_ _____________________
Page 23 of 23
An ice skater rotates in a horizontal plane (around a vertical axis of rotation) as shown in the diagram.
Looking down from above, the skater is rotating in a counter-clockwise direction. With her arms and one leg
outstretched, her moment of inertia is 3.60 kgm2 and she rotates with an angular speed of 2.00 rev/s.
(a) What is the direction of the skater’s angular momentum vector? Circle the correct answer.
(i) Horizontally to the right
(ii) Horizontally to the left
(iii) Vertically down
(iv) Vertically up
(v) Perpendicular to and into the page
(vi) Perpendicular to and out of the page
(vii) None of the above
(b) What is the magnitude of the angular momentum of the skater? Write the answer in SI units.
(c) What is the skater’s rotational kinetic energy? Write the answer in SI units.
(d) The skater now pulls her arms and leg in very close to her body such that her moment of inertia decreases to 0.720 kgm2.
What is the skater’s new rotational speed?
6/25/2017