Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download MAT 0024 5
Document related concepts
Maxwell's equations wikipedia , lookup
Two-body problem in general relativity wikipedia , lookup
Path integral formulation wikipedia , lookup
Two-body Dirac equations wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Schrödinger equation wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Dirac equation wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Equations of motion wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Van der Waals equation wikipedia , lookup
Itô diffusion wikipedia , lookup
Differential equation wikipedia , lookup
Calculus of variations wikipedia , lookup
Exact solutions in general relativity wikipedia , lookup
Transcript
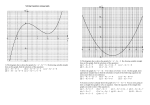
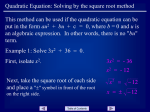
5.7 Solving Polynomial Equations by Factoring A quadratic or second degree equation (highest power of x is 2) is one that may be written in the form ax2 + bx + c = 0, where a 0. Example: x2 – 2x + 4 = 0 Get 0 on one side. 1. x2 –5x = 8 2. 5x2 = 3x 3. x2 = 25 We use the Principle of Zero Products to solve a quadratic equation: AB=0 is true if and only if A=0 or B=0 or both. A product is 0 if and only if at least one factor is 0. Use the Principle of Zero Products to solve these equations: 1. x(x + 3)= 0 2. (x - 4) (3x + 1)= 0 3. x(x + 1) (5x – 2)= 0 To Solve a Quadratic Equation: 1) Get 0 on one side of the equation. Make term of highest degree positive. 2) Factor the other side of the equation. 3) Set each factor equal to 0 and solve for the variable. SOLVE: 1. x2 – 25= 0 2. x2 – x – 12= 0 3. x3 + 14x2 + 24x = 0 4. y2 – 9y = 0 5. w2 – 16 = 0 6. x3 – 3x2 – 10x = 0 7. x2 - x= 20 8. –24 = 6x – 3x2 9. -8x2 = 5x 10. 2x2 – 6x = x 11. 13. 2x3 – 4x2 = 30x 14. 9 = 25y2 x4 + 25 = 26x2 12. 6x = 3x2 15. 3x2 – 13x = 10
