* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 2-5: Complex Numbers
Survey
Document related concepts
Transcript
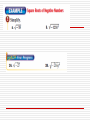
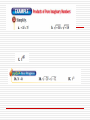
Imaginary & Complex Numbers 5-3 English Casbarro Unit 5: Polynomials Definition: i is defined as . So every negative number under a square root sign can be written as (–1) times the number. Recall: . If you have which equals 5 * Now you try: i = 5i. , you can rewrite it as Sometimes the numbers will need to be factored before a perfect square appears. For example, to Now you try: is not a perfect square. But it will factor = 5* i* =5 i i comes in groups of 4: i=i i =i i = -1 i = –1 i = -i i = -i i =1 i =1 5 2 6 3 7 4 8 So, to find i 542, you would have to figure out where it is in the group of 4 You just need to know the remainder. 4 542 You can also solve equations using imaginary numbers. Example 4 3x2 + 48 = 0 Example 5 x2 = -81 Example 6 3x2 + 75 = 0 A complex number is a number that has both imaginary and real components. It is in the form below: a + bi This is the real part This is the imaginary part Because there are 2 distinct parts, you can make simple equations using the imaginary and the real parts. Example 7 3x + 25i = 15 – 5yi Example 8 2x – 6 i = -8 + 20yi Adding and Subtracting Complex Numbers Complex numbers behave just like the real numbers you have been adding And subtracting. Remember that you must have like terms to combine them. There are more difficult problems that you can solve that depend on your knowing the following factorizations (make sure to check out the pattern!): (x (x (x (x (x (x (x (x (x (x + + + + + + + + + + 1)2 = x2 + 2x + 1 2)2 = x2 + 4x + 4 3)2 = x2 + 6x + 9 4)2 = x2 + 8x + 16 5)2 = x2 + 10x + 25 6)2 = x2 + 12x + 36 7)2 = x2 + 14x + 49 8)2 = x2 + 16x + 64 9)2 = x2 + 18x + 81 10)2 = x2 + 20x + 100 Completing the Square What number would I need to add to the following expressions to keep to the pattern from the previous slide? x2+ 20x + _______ x2 + 24x + _______ x2 + 30x + _______ x2 + 42x + _______ How would you write the factors of these expressions? Now, let’s use what we’ve learned to solve some equations. Example 9 Find the zeroes of each function. a. f(x) = x2 + 2x + 5 b. f(x)= x2 + 10x + 35 Notice that each root is ±. This will always be true when you are taking a square root, so imaginary numbers will always come in pairs, one positive and one negative. Complex numbers have conjugates i 5 + 2 has the conjugate 5 – 2 i The Quadratic Formula For any quadratic equation ax2 + bx + c = 0, the solutions can be found using the following formula. The quadratic formula will work for any quadratic equation, just like completing the square. In fact, the quadratic formula was discovered using the method completing the square. Proving the Quadratic Formula: ax2 + bx + c = 0 Find the number that you have to add to make a perfect square— divide b by 2, and square it– add it to the opposite side also Factor the left side using the square You must get a common denominator on the right side You must get a common denominator on the right side Consolidate the right side into a single fraction Take the square root of both sides Solve for x by moving other side. to the Consolidate the right side into a single fraction