Download 2-5: Complex Numbers

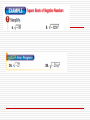
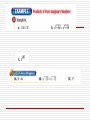
Imaginary & Complex
Numbers
5-3
English Casbarro
Unit 5: Polynomials
Definition:
i
is defined as
. So every negative number under
a square root sign can be written as (–1) times the number.
Recall:
.
If you have
which equals 5 *
Now you try:
i = 5i.
, you can rewrite it as
Sometimes the numbers will need to be factored before a perfect square
appears. For example,
to
Now you try:
is not a perfect square. But it will factor
= 5*
i*
=5
i
i comes in groups of 4:
i=i
i =i
i = -1
i = –1
i = -i
i = -i
i =1
i =1
5
2
6
3
7
4
8
So, to find
i
542,
you would have to figure out
where it is in the group of 4
You just need to know the
remainder.
4 542
You can also solve equations using imaginary numbers.
Example 4
3x2 + 48 = 0
Example 5
x2 = -81
Example 6
3x2 + 75 = 0
A complex number is a number that has
both imaginary and real components. It is
in the form below:
a + bi
This is the
real part
This is the
imaginary part
Because there are 2 distinct parts, you can make simple
equations using the imaginary and the real parts.
Example 7
3x + 25i = 15 – 5yi
Example 8
2x – 6
i = -8 + 20yi
Adding and Subtracting Complex
Numbers
Complex numbers behave just like the real numbers you have been adding
And subtracting. Remember that you must have like terms to combine them.
There are more difficult problems that you can solve
that depend on your knowing the following
factorizations (make sure to check out the pattern!):
(x
(x
(x
(x
(x
(x
(x
(x
(x
(x
+
+
+
+
+
+
+
+
+
+
1)2 = x2 + 2x + 1
2)2 = x2 + 4x + 4
3)2 = x2 + 6x + 9
4)2 = x2 + 8x + 16
5)2 = x2 + 10x + 25
6)2 = x2 + 12x + 36
7)2 = x2 + 14x + 49
8)2 = x2 + 16x + 64
9)2 = x2 + 18x + 81
10)2 = x2 + 20x + 100
Completing the Square
What number would I need to add to
the following expressions to keep to
the pattern from the previous slide?
x2+ 20x + _______
x2 + 24x + _______
x2 + 30x + _______
x2 + 42x + _______
How would you write the factors of these
expressions?
Now, let’s use what we’ve learned to solve some equations.
Example 9
Find the zeroes of each function.
a. f(x) = x2 + 2x + 5
b. f(x)= x2 + 10x + 35
Notice that each root is ±. This will always be true when you are taking a
square root, so imaginary numbers will always come in pairs, one positive and
one negative. Complex numbers have conjugates
i
5 + 2 has the conjugate 5 – 2
i
The Quadratic Formula
For any quadratic equation ax2 + bx + c = 0,
the solutions can be found using the
following formula.
The quadratic formula will work for any quadratic equation, just like
completing the square. In fact, the quadratic formula was discovered
using the method completing the square.
Proving the Quadratic Formula:
ax2 + bx + c = 0
Find the number that you have to
add to make a perfect square—
divide b by 2, and square it– add it
to the opposite side also
Factor the left side using the square
You must get a common denominator on
the right side
You must get a common denominator on
the right side
Consolidate the right side into
a single fraction
Take the square root of both sides
Solve for x by moving
other side.
to the
Consolidate the right side into
a single fraction