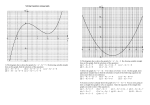
Download Chapter 22 Problem 66 † Given V (x)=3x - 2x 2

Chapter 22
Problem 66
†
Given
V (x) = 3x − 2x2 − x3
Solution
a) Find the locations where the potential is zero.
Factor the potential function as much as possible.
V (x) = x(3 − 2x − x2 )
V (x) = x(3 + x)(1 − x)
The only places where the potential is equal to zero is when one of its factors is equal to zero. Therefore,
Either x = 0, 3 + x = 0, or 1 − x = 0 From these 3 equations we get
x = −3 m, 0 m, 1 m
b) Find the electric field function in the x direction.
The electric field in the x direction is given by
Ex = −
d(3x − 2x2 − x3 )
dV
=−
dx
dx
Ex = −(3 − 4x − 3x2 ) = −3 + 4x + 3x2
c) Find the locations where the electric field is zero.
Setting the electric field to zero gives
−3 + 4x + 3x2 = 0
Use the quadratic formula to find the zeros of the function.
p
−(4) ± (4)2 − 4(3)(−3)
x=
2(3)
√
√
−4 ± 52
−2 ± 13
x=
=
6
3
x = −1.87 m, 0.535 m
†
Problem from Essential University Physics, Wolfson