Download Euclidean Geometry

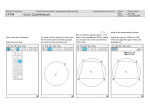
Zhijing Chen
Cyclic Quadrilaterals Theorems
This project introdeced us the theorems about cyclic quadrilaterals.
According to these three theorems, we could find out some interesting results about
the cyclic quadrilaterals. And the key point of all the proofs is based on the attributes of
circumscribed triangles: If two triangles have a same circumscribed circle , and they
have congruent sides, the opposite angles of the side are congruent.
1. Here I would like to re-present the second theorem of this theorem first because it
helps define what a cyclic quadrilateral is.
“The sum of the opposite angles of a cyclic quadrilateral is 180 degree.”
Here are four different quadrilaterals with the same length of sides.
But only two of them( upper two quadrilaterals) are cyclic quadrilaterals by this
theorem.
2. Ptolemy's Theorem:
The sum of the products of its two pairs of opposite sides is equal to the product of its
diagonals.
Ptolemy’s Theorem leads a way to find out the hidden connection of cyclic
quadrilaterals.
3. if a cyclic quadrilateral has perpendicular diagonals, then the perpendicular to a side
from the point of intersection of the diagonals always bisects the opposite side.
This theorem reminds me another proof of the formula in Trigonometry,
Assume a,b,c are the sides of a triangle; A,B,C are the three angles. Then we know
the area of the triangle is:
S=1/2 ab sin C
=1/2 ac sin B
=1/2 bc sin A
Plus, we know:
a2 = b2 + c2 − 2bc cosA
b2 = c2 + a2 − 2ca cosB
c2 = a2 + b2 − 2ab cosC
If we use s for the perimeter of a triangle, then we can get:
S2 = qs(s − a)(s − b)(s − c)
(s = 1/2 (a + b + c))
Diagram for Projective Plane in Order 2
Michael River and Wesley Parker’s project introduces the finite projective planes and
finite fields. A projective plane coodinatized by a finite field exists for all prime power
orders. Here is the table for projective plane in order 2----the smallest prime. I will show
how to use the table to construct the Fano Plane.
Points:
Lines:
(0,0,1)n
(0,1,0)o
(0,1,1)p
(1,0,0)q
(1,0,1)r
(1,1,0)s
(1,1,1)t
(0,0,1)
A
1
0
1
0
1
0
1
(0,1,0)
B
0
1
1
0
0
1
1
(0,1,1)
C
1
1
0
0
1
1
0
(1,0,0)
D
0
0
0
1
1
1
1
(1,0,1)
E
1
0
1
1
0
1
0
(1,1,0)
F
0
1
1
1
1
0
0
(1,1,1)
G
1
1
0
1
0
0
1
Those points are named by letters from A to G; while the lines are named by letter from
n to t.
The Fano Plane is a four-point plane( see diagram below).
When we start to construct this plane, the number “0” means the point is incident with the
line. So now, we can get the plane like the diagram below: