Download Presentation: Cyclic Quadrilaterals

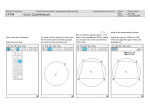
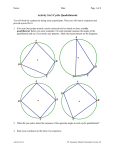
Euclidean and Non-Euclidean Geometry – Fall 2007
Dr. Hamblin
Presentation: Cyclic Quadrilaterals
In this presentation, you will investigate a special class of quadrilaterals known as “cyclic quadrilaterals.”
By definition, a cyclic quadrilateral is one where all four vertices lie on a single circle.
Using Sketchpad, investigate cyclic quadrilaterals and verify the following
facts (you will prove these later):
The opposite angles of a cyclic quadrilateral are supplementary.
The perpendicular bisectors of the sides of a cyclic quadrilateral are
always concurrent at the center of the circle.
Proofs
In order to prove these statements, we will need to use the Inscribed Angle
Theorem (p. 270 in your book). This theorem states that the measure of an
inscribed angle is equal to half of the measure of its intercepted arc.
As part of your presentation, you should include the following.
Explain briefly why the Inscribed Angle Theorem is true.
Use the Inscribed Angle Theorem to prove that the opposite angles
of a cyclic quadrilateral are supplementary.
Explain why the perpendicular bisectors of each of the four sides passes through the center of
the circle. Draw a line segment connecting opposite vertices to split the quadrilateral into two
triangles. Then use the result of Problem #20 from Section 3.3.
Converse
So far, you have proved that if a quadrilateral is cyclic, then its opposite angles are supplementary. Now
we will prove that if a quadrilateral has the property that a pair of opposite angles is supplementary,
then it must be cyclic.
We will prove this by contradiction: Suppose that quadrilateral
has the property that opposite
angles are supplementary, specifically that
and
are supplementary. However, suppose
also that
is not cyclic. Follow this outline to complete the proof.
Since
is not cyclic, the circumcircle of
does not pass
through . For now, assume that lies outside of this circle. We will
consider the other case later.
Euclidean and Non-Euclidean Geometry – Fall 2007
Dr. Hamblin
Since lies outside the circle, either
or
meets the circle. Without loss of generality,
suppose
meets the circle at . (You should use Sketchpad to illustrate the case where
does not meet the circle.)
What kind of quadrilateral is
?
From what you already proved about cyclic quadrilaterals, what is the relationship between
and
?
What do you already know about the relationship between
tell you about
and
?
Draw segment
and
? What does this
, and use the Exterior Angle Theorem to reach a contradiction.
You should now consider the case where is inside the circle. The argument should be similar,
involving the facts you have already proved about cyclic quadrilaterals and the Exterior Angle Theorem.
Further Investigation: Cyclic Polygons
We can extend the definition of cyclic to pentagons, hexagons, and so on. What
can you say about the measures of the angles of these kinds of polygons? Make a
conjecture and prove that it is correct.