Algebraic semantics for predicate logics and their completeness
... Algebraic semantics for nonclassical propositional logics provides us a powerful tool in studying logical properties which are common among many logics. In fact, it has been producing a lot of interesting general results by the help of universal algebraic methods. On the other hand, it seems that th ...
... Algebraic semantics for nonclassical propositional logics provides us a powerful tool in studying logical properties which are common among many logics. In fact, it has been producing a lot of interesting general results by the help of universal algebraic methods. On the other hand, it seems that th ...
Algebra - University at Albany
... the exactness properties of tensor and hom. In Section 9.3, Hilbert’s Nullstellensatz is proven, using many of the tools so far developed, and is used to define algebraic varieties. In Section 9.5, extension of rings is used to extend some of the standard results about injections and surjections betw ...
... the exactness properties of tensor and hom. In Section 9.3, Hilbert’s Nullstellensatz is proven, using many of the tools so far developed, and is used to define algebraic varieties. In Section 9.5, extension of rings is used to extend some of the standard results about injections and surjections betw ...
Affine group schemes over symmetric monoidal categories
... 2009]. It is therefore natural to ask whether arithmetic geometry can be similarly developed in the general framework of symmetric monoidal categories. In particular, since the theory of finite flat group schemes is closely linked to arithmetic (see [Tate 1997], for instance), they are a natural sta ...
... 2009]. It is therefore natural to ask whether arithmetic geometry can be similarly developed in the general framework of symmetric monoidal categories. In particular, since the theory of finite flat group schemes is closely linked to arithmetic (see [Tate 1997], for instance), they are a natural sta ...
Greenwich Public Schools Mathematics Curriculum Objectives
... The measures of geometric figures can be calculated and analyzed using a variety of strategies, tools, and technologies. A change in one dimension of an object results in predictable changes in area and or ...
... The measures of geometric figures can be calculated and analyzed using a variety of strategies, tools, and technologies. A change in one dimension of an object results in predictable changes in area and or ...
COMMUTATIVE ALGEBRA Contents Introduction 5 0.1. What is
... In these notes we will be (almost) always working in the category of commutative rings with unity. In a sense which will shortly be made precise, this means that the identity 1 is regarded as part of the structure of a ring and must therefore be preserved by all homomorphisms. Probably it would be m ...
... In these notes we will be (almost) always working in the category of commutative rings with unity. In a sense which will shortly be made precise, this means that the identity 1 is regarded as part of the structure of a ring and must therefore be preserved by all homomorphisms. Probably it would be m ...
Fun with Fields by William Andrew Johnson A dissertation submitted
... • Fields, and valued fields in particular • Theories without the independence property (NIP theories) • Elimination of imaginaries The most important result is a classification of dp-minimal fields, presented in Chapter 9. Recall that dp-rank is a notion of “rank” or “dimension” that is particularly ...
... • Fields, and valued fields in particular • Theories without the independence property (NIP theories) • Elimination of imaginaries The most important result is a classification of dp-minimal fields, presented in Chapter 9. Recall that dp-rank is a notion of “rank” or “dimension” that is particularly ...
Abstract Algebra - UCLA Department of Mathematics
... multiply them by scalars. In abstract algebra, we attempt to provide lists of properties that common mathematical objects satisfy. Given such a list of properties, we impose them as “axioms”, and we study the properties of objects that satisfy these axioms. The objects that we deal with most in the ...
... multiply them by scalars. In abstract algebra, we attempt to provide lists of properties that common mathematical objects satisfy. Given such a list of properties, we impose them as “axioms”, and we study the properties of objects that satisfy these axioms. The objects that we deal with most in the ...
Wedhorn, Adic spaces
... The product order on i∈I Γi (i.e., (γi )i ≤ (γi0 )i if and only if γi ≤ γi0 for all i ∈ I) is not a total order (except if there exists only one index i such that Γi 6= {1}). (4) More generally, let I be a totally ordered index set and let (Γi )i∈I be a family of totally ordered Q groups. We define ...
... The product order on i∈I Γi (i.e., (γi )i ≤ (γi0 )i if and only if γi ≤ γi0 for all i ∈ I) is not a total order (except if there exists only one index i such that Γi 6= {1}). (4) More generally, let I be a totally ordered index set and let (Γi )i∈I be a family of totally ordered Q groups. We define ...
Algebra 2 - Adventist Education
... Simplify expressions using the order of operations, including radicals and absolute value. N-RN.1,2, NCN.1,2 ...
... Simplify expressions using the order of operations, including radicals and absolute value. N-RN.1,2, NCN.1,2 ...
Notes
... Let’s go back to the analogy between function fields and number fields. In the function field context, we have moduli spaces of shtukas. These are associated to data (G, {µ1 , . . . , µm }) where G is a reductive group and the µi are conjugacy classes of cocharacters of G (over an algebraic closure) ...
... Let’s go back to the analogy between function fields and number fields. In the function field context, we have moduli spaces of shtukas. These are associated to data (G, {µ1 , . . . , µm }) where G is a reductive group and the µi are conjugacy classes of cocharacters of G (over an algebraic closure) ...
Symplectic structures -- a new approach to geometry.
... where the flux group Γω is a subgroup of H 1 (M, R). Example. In the case of the torus T 2 with a symplectic form dx ∧ dy of total area 1, the group Γω is H 1 (M, Z). The family of rotations Rt : (x, y) 7→ (x+t, y) of the torus T 2 consists of symplectomorphisms that are not Hamiltonian. Its image u ...
... where the flux group Γω is a subgroup of H 1 (M, R). Example. In the case of the torus T 2 with a symplectic form dx ∧ dy of total area 1, the group Γω is H 1 (M, Z). The family of rotations Rt : (x, y) 7→ (x+t, y) of the torus T 2 consists of symplectomorphisms that are not Hamiltonian. Its image u ...
An Introduction to Algebraic Number Theory, and the Class Number
... We describe various algebraic invariants of number fields, as well as their applications. These applications relate to prime ramification, the finiteness of the class number, cyclotomic extensions, and the unit theorem. Finally, we present an exposition of the class number formula, which generalizes ...
... We describe various algebraic invariants of number fields, as well as their applications. These applications relate to prime ramification, the finiteness of the class number, cyclotomic extensions, and the unit theorem. Finally, we present an exposition of the class number formula, which generalizes ...
Hovhannes Khudaverdian's notes
... Make the lexicographic ordering in the space of polynomials. It is like in dictionary: xp is higher than xq if p > q. Monomial xa1 1 . . . xann is higher than monomial xb11 . . . xbnn if a1 > b1 . If a1 = b1 we have to look at the degree of the second variable x2 : If a1 = b1 and a2 > b2 then monomi ...
... Make the lexicographic ordering in the space of polynomials. It is like in dictionary: xp is higher than xq if p > q. Monomial xa1 1 . . . xann is higher than monomial xb11 . . . xbnn if a1 > b1 . If a1 = b1 we have to look at the degree of the second variable x2 : If a1 = b1 and a2 > b2 then monomi ...
Noncommutative geometry @n
... Ever since the dawn of noncommutative algebraic geometry in the midseventies, see for example the work of P. Cohn [21], J. Golan [38], C. Procesi [86], F. Van Oystaeyen and A. Verschoren [103],[105], it has been ring theorists’ hope that this theory might one day be relevant to commutative geometry, ...
... Ever since the dawn of noncommutative algebraic geometry in the midseventies, see for example the work of P. Cohn [21], J. Golan [38], C. Procesi [86], F. Van Oystaeyen and A. Verschoren [103],[105], it has been ring theorists’ hope that this theory might one day be relevant to commutative geometry, ...
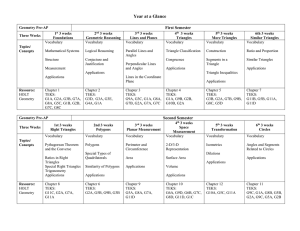
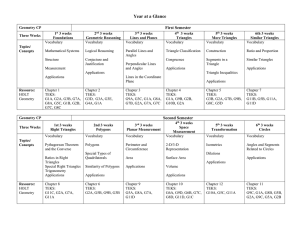
Geometry Pre AP Scope and Sequence
... Investigate properties of similar triangles Construct statements related to triangle similarity relationships Determine necessary and sufficient conditions in order for triangles to be similar Use logical reasoning to justify triangle similarity from a variety of perspectives Apply propert ...
... Investigate properties of similar triangles Construct statements related to triangle similarity relationships Determine necessary and sufficient conditions in order for triangles to be similar Use logical reasoning to justify triangle similarity from a variety of perspectives Apply propert ...
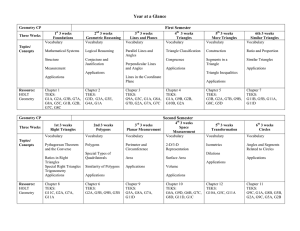
Geometry CP Scope and Sequenc
... based on the number of their sides or angles. Use a variety of methods to investigate the interior and exterior angle relationships of polygons Make and justify conjectures about component parts of polygons Investigate necessary conditions for polygons to be identified as “regular” Make and ...
... based on the number of their sides or angles. Use a variety of methods to investigate the interior and exterior angle relationships of polygons Make and justify conjectures about component parts of polygons Investigate necessary conditions for polygons to be identified as “regular” Make and ...
kucukarslan et al.
... membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical structures and to study properties of these fuzzy objects. Many scientists have studied fuz ...
... membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical structures and to study properties of these fuzzy objects. Many scientists have studied fuz ...
Varieties of cost functions
... Related work Toruńczyk [28] also established a link between cost functions and profinite words, using a different approach. More precisely, Toruńczyk identifies a regular cost function with the set of profinite words that are limits of infinite sequences of words over which the function is bounded ...
... Related work Toruńczyk [28] also established a link between cost functions and profinite words, using a different approach. More precisely, Toruńczyk identifies a regular cost function with the set of profinite words that are limits of infinite sequences of words over which the function is bounded ...
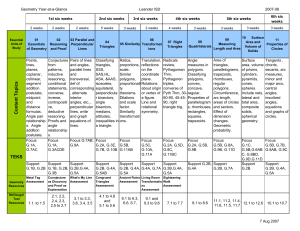
Mapping for Instruction - First Nine Weeks
... resource. It is extremely important and required that the Sequence of Instruction and Pacing be followed as presented in the curriculum guide. This will allow the formative assessment tests to be an effective instructional tool. Students will take a formative assessment test during the second, third ...
... resource. It is extremely important and required that the Sequence of Instruction and Pacing be followed as presented in the curriculum guide. This will allow the formative assessment tests to be an effective instructional tool. Students will take a formative assessment test during the second, third ...
TEKS Content Topics
... (B) recognize the historical development of geometric systems and know mathematics is developed for a variety of purposes. - line segment ...
... (B) recognize the historical development of geometric systems and know mathematics is developed for a variety of purposes. - line segment ...
Non-euclidean shadows of classical projective
... We claim that there are enough reasons for this line to deserve the name Euler line. Giving credit to [24], we will call it Euler-Wildberger line. Some of the classical centers of an euclidean triangle can be defined in multiple ways, all of them equivalent. However, two such definitions, equivalent ...
... We claim that there are enough reasons for this line to deserve the name Euler line. Giving credit to [24], we will call it Euler-Wildberger line. Some of the classical centers of an euclidean triangle can be defined in multiple ways, all of them equivalent. However, two such definitions, equivalent ...
Algebraic variety

In mathematics, algebraic varieties (also called varieties) are one of the central objects of study in algebraic geometry. Classically, an algebraic variety was defined to be the set of solutions of a system of polynomial equations, over the real or complex numbers. Modern definitions of an algebraic variety generalize this notion in several different ways, while attempting to preserve the geometric intuition behind the original definition.Conventions regarding the definition of an algebraic variety differ slightly. For example, some authors require that an ""algebraic variety"" is, by definition, irreducible (which means that it is not the union of two smaller sets that are closed in the Zariski topology), while others do not. When the former convention is used, non-irreducible algebraic varieties are called algebraic sets.The notion of variety is similar to that of manifold, the difference being that a variety may have singular points, while a manifold will not. In many languages, both varieties and manifolds are named by the same word.Proven around the year 1800, the fundamental theorem of algebra establishes a link between algebra and geometry by showing that a monic polynomial (an algebraic object) in one variable with complex coefficients is determined by the set of its roots (a geometric object) in the complex plane. Generalizing this result, Hilbert's Nullstellensatz provides a fundamental correspondence between ideals of polynomial rings and algebraic sets. Using the Nullstellensatz and related results, mathematicians have established a strong correspondence between questions on algebraic sets and questions of ring theory. This correspondence is the specificity of algebraic geometry among the other subareas of geometry.