
What is Hyperbolic Geometry? - School of Mathematics, TIFR
... A finite straight line may be extended continuously in a straight line. ...
... A finite straight line may be extended continuously in a straight line. ...
What is Hyperbolic Geometry?
... A finite straight line may be extended continuously in a straight line. ...
... A finite straight line may be extended continuously in a straight line. ...
On Lobachevsky`s trigonometric formulae
... details, and highlighting applications of his work outside the world of pure geometry,6 with the hope of attracting the attention of his colleagues. His efforts in that direction were vain, and his work was acknowledged only ten years after his death. These memoirs that he left, despite the fact tha ...
... details, and highlighting applications of his work outside the world of pure geometry,6 with the hope of attracting the attention of his colleagues. His efforts in that direction were vain, and his work was acknowledged only ten years after his death. These memoirs that he left, despite the fact tha ...
On Lobachevsky`s trigonometric formulae
... details, and highlighting applications of his work outside the world of pure geometry,6 with the hope of attracting the attention of his colleagues. His efforts in that direction were vain, and his work was acknowledged only ten years after his death. These memoirs that he left, despite the fact tha ...
... details, and highlighting applications of his work outside the world of pure geometry,6 with the hope of attracting the attention of his colleagues. His efforts in that direction were vain, and his work was acknowledged only ten years after his death. These memoirs that he left, despite the fact tha ...
File
... If TWO SIDES and the INCLUDED ANGLE of one Triangle are CONGRUENT to TWO SIDES and the INCLUDED ANGLE of another Triangle THEN ...
... If TWO SIDES and the INCLUDED ANGLE of one Triangle are CONGRUENT to TWO SIDES and the INCLUDED ANGLE of another Triangle THEN ...
Slides for Nov. 12, 2014, lecture
... Euclid’s Fifth Postulate 5. If one straight line falling on two straight lines makes the interior angles in the same direction less than two right angles, then the two straight lines, if produced in infinitum, meet one another in that direction in which the angles less than two right angles are. ...
... Euclid’s Fifth Postulate 5. If one straight line falling on two straight lines makes the interior angles in the same direction less than two right angles, then the two straight lines, if produced in infinitum, meet one another in that direction in which the angles less than two right angles are. ...
math 260 perspectives in geometry
... where d1 and d2 are the lengths of the diagonals. 31. A square is a quadrilateral that is both a rhombus and a rectangle. Cool Fact 29 If a rhombus has one right angle, then it is a square. Cool Fact 30 Since a square is a rhombus, then we can compute its area using its diagonals. 32. A trapezoid is ...
... where d1 and d2 are the lengths of the diagonals. 31. A square is a quadrilateral that is both a rhombus and a rectangle. Cool Fact 29 If a rhombus has one right angle, then it is a square. Cool Fact 30 Since a square is a rhombus, then we can compute its area using its diagonals. 32. A trapezoid is ...
geometry - Calculate
... This is a terrific website: Art and Mathematics http://www.math.nus.edu.sg/aslaksen/teaching/math-art-arch.shtml ...
... This is a terrific website: Art and Mathematics http://www.math.nus.edu.sg/aslaksen/teaching/math-art-arch.shtml ...
Triangles in Hyperbolic Geometry
... model results in slightly different definitions for lines, distance and area. A useful tool when working in the Poincaré model is the transformation of inversion and its effects on objects in the Hyperbolic plane. 3.1. Alternatives to Euclid’s Parallel Postulate. Depending on what axioms are used, ...
... model results in slightly different definitions for lines, distance and area. A useful tool when working in the Poincaré model is the transformation of inversion and its effects on objects in the Hyperbolic plane. 3.1. Alternatives to Euclid’s Parallel Postulate. Depending on what axioms are used, ...
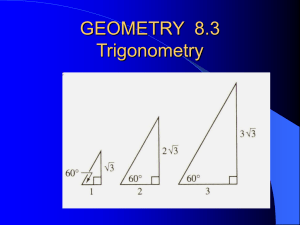
GEOMETRY 8.3 Trigonometry
... He can Calculate ALL three (Equations) Thank you SOHCAHTOA I’m Really Glad to Know Ya You’re the CHIEF of Trigonometry ...
... He can Calculate ALL three (Equations) Thank you SOHCAHTOA I’m Really Glad to Know Ya You’re the CHIEF of Trigonometry ...
A Brief History of the Fifth Euclidean Postulate and Two New Results
... theorem is to be found in Baudhayana’s ( 800 BC ). The chord which is stretched across the diagram of a square produces an area of double the size. The earliest recorded beginnings of geometry can be traced to ancient Mesopotamia, Egypt, and the Indus Valley from around 3000 BC. Early geometry was a ...
... theorem is to be found in Baudhayana’s ( 800 BC ). The chord which is stretched across the diagram of a square produces an area of double the size. The earliest recorded beginnings of geometry can be traced to ancient Mesopotamia, Egypt, and the Indus Valley from around 3000 BC. Early geometry was a ...
On characterizations of Euclidean spaces
... arbitrarily chosen unit) of the corresponding sector of the unit circle (normalized to 2π). This also defines an angular bisector. ...
... arbitrarily chosen unit) of the corresponding sector of the unit circle (normalized to 2π). This also defines an angular bisector. ...
Page 1 of 1 Geometry, Student Text and Homework Helper 11/7
... 11. Create Representations to Communicate Mathematical Ideas (1)(E) In spherical geometry how many perpendicular line segments can you draw from a point to a line? Draw a sketch to support your answer. ...
... 11. Create Representations to Communicate Mathematical Ideas (1)(E) In spherical geometry how many perpendicular line segments can you draw from a point to a line? Draw a sketch to support your answer. ...
[edit] Construction of the Lebesgue measure
... you can even take one real number into two continuously, so that a one-dimensional object can completely fill up a higher dimensional object. Every space filling curve hits every point many times, and does not have a continuous inverse. It is impossible to map two dimensions onto one in a way that i ...
... you can even take one real number into two continuously, so that a one-dimensional object can completely fill up a higher dimensional object. Every space filling curve hits every point many times, and does not have a continuous inverse. It is impossible to map two dimensions onto one in a way that i ...
Geometry 4.1 Some DEFINITIONS POLYGON
... Definition: EXTERIOR ANGLE An Exterior Angle is formed by one side of a triangle and the extension of another side. Definition: REMOTE INTERIOR ANGLES The Interior Angles of the Triangle NOT adjacent to a given Exterior Angle are Remote Interior Angles. ...
... Definition: EXTERIOR ANGLE An Exterior Angle is formed by one side of a triangle and the extension of another side. Definition: REMOTE INTERIOR ANGLES The Interior Angles of the Triangle NOT adjacent to a given Exterior Angle are Remote Interior Angles. ...
lesson 3.3 Geometry.notebook
... Use the angles formed by a transversal to prove two lines are parallel. Today we are doing the converse of last class! ...
... Use the angles formed by a transversal to prove two lines are parallel. Today we are doing the converse of last class! ...
GEOMETRY FINAL REVIEW - Lakeside High School
... GEOMETRY FINAL REVIEW-ch. 2 The given statement is a valid geometric proposition. Statement: If a triangle has two congruent angles, then it is an isosceles triangle. a) Write the contrapositive of this statement: b) NOW, Determine if the contrapositive statement is valid. Explain your reasoning. ...
... GEOMETRY FINAL REVIEW-ch. 2 The given statement is a valid geometric proposition. Statement: If a triangle has two congruent angles, then it is an isosceles triangle. a) Write the contrapositive of this statement: b) NOW, Determine if the contrapositive statement is valid. Explain your reasoning. ...
Introduction to Hyperbolic Geometry - Conference
... negation, which we shall call the „Hyperbolic Parallel Axiom' " . Returning to the definition of Hyperbolic Geometry, two parts were emphasized. First, the axioms of Neutral Geometry, which consist of the theorems that can be proven without the use of the fifth postulate, are included in Hyperbolic ...
... negation, which we shall call the „Hyperbolic Parallel Axiom' " . Returning to the definition of Hyperbolic Geometry, two parts were emphasized. First, the axioms of Neutral Geometry, which consist of the theorems that can be proven without the use of the fifth postulate, are included in Hyperbolic ...
Contents 1 2 9
... of blue prints and building. Using the same blue prints, one can build different sized models, or real buildings, in wood, steel, or plastic, for example. Ther are two benefits: To understand how all these buildings work, one really just have to study their common blue print carefully. Or since they ...
... of blue prints and building. Using the same blue prints, one can build different sized models, or real buildings, in wood, steel, or plastic, for example. Ther are two benefits: To understand how all these buildings work, one really just have to study their common blue print carefully. Or since they ...
Homography
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which they are derived. It is a bijection that maps lines to lines, and thus a collineation. In general, there are collineations which are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation.Historically, homographies (and projective spaces) have been introduced to study perspective and projections in Euclidean geometry, and the term ""homography"", which, etymologically, roughly means ""similar drawing"" date from this time. At the end of 19th century, formal definitions of projective spaces were introduced, which differed from extending Euclidean or affine spaces by adding points at infinity. The term ""projective transformation"" originated in these abstract constructions. These constructions divide into two classes that have been shown to be equivalent. A projective space may be constructed as the set of the lines of a vector space over a given field (the above definition is based on this version); this construction facilitates the definition of projective coordinates and allows using the tools of linear algebra for the study of homographies. The alternative approach consists in defining the projective space through a set of axioms, which do not involve explicitly any field (incidence geometry, see also synthetic geometry); in this context, collineations are easier to define than homographies, and homographies are defined as specific collineations, thus called ""projective collineations"".For sake of simplicity, unless otherwise stated, the projective spaces considered in this article are supposed to be defined over a (commutative) field. Equivalently Pappus's hexagon theorem and Desargues' theorem are supposed to be true. A large part of the results remain true, or may be generalized to projective geometries for which these theorems do not hold.
















![[edit] Construction of the Lebesgue measure](http://s1.studyres.com/store/data/001141507_1-534aa5aeea25b32a8226835f0ebc16e0-300x300.png)





