Download math 260 perspectives in geometry

California State University, Fresno
MATH 260
PERSPECTIVES IN GEOMETRY
Spring 2011
Instructor : Stefaan Delcroix
Author: Oscar Vega
Contents
1 Things you should know
The essentials, on the plane . .
Congruency . . . . . . . . . . .
Polygons . . . . . . . . . . . . .
Circles . . . . . . . . . . . . . .
3 − D geometry . . . . . . . . .
The Cartesian plane and conics
Exercises . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
2
5
5
12
16
17
19
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . .
. . . . . . .
in geometry
. . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
25
27
30
33
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
35
36
39
41
45
4 Basic neutral geometry
Euclid’s Elements . . . . . . . . . . . . . . . . .
Definitions . . . . . . . . . . . . . . . . . .
Common Notions . . . . . . . . . . . . . .
Postulates . . . . . . . . . . . . . . . . . .
The first 28 propositions . . . . . . . . . .
Saccheri-Khayyam and Lambert quadrilaterals
Equivalent to the fifth . . . . . . . . . . . . . .
Exercises . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
47
47
47
48
49
49
55
60
65
2 Measuring is overrated
A.K.A Size does not matter
Affine planes . . .
Projective planes .
Other measure-free
Exercises . . . . .
. . . .
. . . .
results
. . . .
3 Cylinders, cones, spheres,
The sphere . . . . . . . . . .
Cylinders and cones . . . . .
Covers . . . . . . . . . . . . .
Exercises . . . . . . . . . . .
24
etc.
. . .
. . .
. . .
. . .
.
.
.
.
.
.
.
.
5 Non-Euclidean Geometries
66
Hyperbolic Geometry . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
The real projective plane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
6 Dissections
76
Parallel transport and holonomy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
Dissection of polygons. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
1
Chapter 1
Things you should know
What follows is just a list of things you should know, we will re-explore many of these concepts in much
more depth later in the semester. Most of the proofs of the facts listed are left as exercises for you, although
we might go over many of them during the semester.
The essentials, on the plane
1. We may think of a point as a dot on a piece of paper. A point has no length or width, it just specifies
an exact location.
2. We may think of a line as a “straight” line that we might draw with a ruler on a piece of paper, except
that in geometry, a line extends forever in both directions. A line passing through two different points
←→
A and B is written as AB.
Any two points determine a unique line.
3. Three or more points are said to be collinear if there is a line that contains them.
P
Q
R
l
Figure 1.1: P , Q and R are collinear points
4. Three or more lines are concurrent if they all pass through the same point.
l
m
n
Figure 1.2: l, m and n are concurrent lines
5. A ray is the portion of a line that has one endpoint and extends indefinitely from the endpoint on. A
−−→
←−−
ray with endpoint A and passing through a point B is written as AB or BA.
−−→
−→
6. The rays AB and AC are opposite rays if they are distinct and the points A, B and C are collinear.
2
CHAPTER 1. THINGS YOU SHOULD KNOW
3
Cool Fact 1 Opposite rays form a 180o angle
7. A line segment is the portion of a line that is between two points. A line segment with endpoints A
and B is written as AB.
8. The length of the segment AB is the distance between A and B. Two segments, AB and CD, having
the same length are said to be congruent. We denote that as AB ∼
= CD.
9. A point P between A and B such that AP ∼
= P B is called the midpoint of the segment AB. The
midpoint is said to bisect the segment.
Cool Fact 2 Given a segment, its midpoint is unique.
10. A bisector of a segment is a line that passes through the midpoint of the segment. If the bisector
intersect the given line forming a 90o angle, then it is called a perpendicular bisector.
l
R
P
Q
Figure 1.3: l is the perpendicular bisector of P Q. R is the midpoint of P Q
Cool Fact 3 Given a segment, its perpendicular bisector is unique.
−−→
−→
11. An angle with vertex A is a point together with two rays AB and AC (called the sides of the angle)
emanating from A. We call this angle ∠BAC or ∠CAB. Often we will use lowercase greek letters to
denote angles.
12. Two angles with a common vertex and that share a side are said to be adjacent angles.
13. Vertical angles are two nonadjacent angles formed by two intersecting lines.
Cool Fact 4 Vertical angles are congruent (Vertical Angle Theorem).
l
m
"
!
Figure 1.4: α and β are vertical angles
14. An acute angle is an angle whose measure is greater than 0o and less than 90o .
15. A right angle has measure exactly 90o .
16. An obtuse angle is an angle whose measure is greater than 90o and less than 180o .
17. A straight angle has measure exactly 180o .
CHAPTER 1. THINGS YOU SHOULD KNOW
4
18. Two angles are called complementary if the sum of their measures is exactly 90o
19. Two angles are called supplementary if the sum of their measures is exactly 180o
Cool Fact 5 Two complementary (or supplementary) angles need not to be adjacent.
20. Congruent angles are angles of the same measure.
21. An angle bisector is a ray whose endpoint is the vertex of the angle and which divides the angle into
two congruent angles.
−−→
In the picture, if α = β, then BD is a bisector of ∠ABC.
D
A
!
"
B
C
Cool Fact 6 Given an angle, its angle bisector is unique.
22. A linear pair of angles are adjacent angles whose non-common sides are opposite rays (form a
straight line).
Cool Fact 7 Two angles that form a linear pair are supplementary of each other.
23. Two lines ` and m are perpendicular if they intersect at a point P and if there is a ray that is part of
` and a ray that is a part of m that form a right angle. Perpendicular lines ` and m are denoted by
` ⊥ m.
24. Two lines in the same plane which never intersect are called parallel lines. We say that two line
segments are parallel if the lines that they lie on are parallel. If `1 and `2 are parallel we write `1 ||`2 .
Two distinct lines that are not parallel intersect in a unique point.
Cool Fact 8 If one throws a perpendicular to, let us say, `1 at ANY point P ∈ `1 , then the segment
created ‘between’ the lines `1 and `2 has always the same length, independently of the point P .
25. Let `1 ||`2 and m a transversal to both of them forming eight angles, like in the following picture,
m
%
'
"
!
#
$
&
l1
(
l2
Then, α = δ = = ϕ and β = γ = φ = ψ.
26. If two lines `1 and `2 are such that there is a transversal m as in the picture above with α = or δ = ϕ
or β = φ or γ = ψ then `1 ||`2 .
27. Given a line ` and point P ∈
/ ` there is a unique parallel line to ` through P .
CHAPTER 1. THINGS YOU SHOULD KNOW
5
Congruency
When we have two figures/shapes that overlap perfectly once one of them is placed on top of the other we
will say that the shapes are congruent. The symbol for ‘congruent to’ is ∼
=.
Since most of the times we will not have the chance to take one shape and place it on top of the other,
then we need criteria to decide when figures are congruent. For example,
1. Two segments are congruent if they have the same length.
2. Two angles are congruent if they have the same measure.
3. Two circles are congruent if they have the same radius.
Congruence of more complicated shapes will be listed in the following sections.
One important thing to remark about congruency is that it is transitive. That is, if A, B and C are
figures/shapes such that A ∼
= B and B ∼
= C, then A ∼
= C.
Polygons
1. A polygon is a set/shape formed by vertices and sides such that every vertex is the endpoint of exactly
two sides.
Note that this definition includes shapes such as
which is a polygon with 5 vertices and 5 sides.
A polygon with sides intersecting only at vertices is called a simple polygon.
Now, a figure such as
A
C
D
B
is also a polygon, but it is not what we usually consider as a polygon.
A convex polygon is a polygon with interior angles measuring less than 180o (this is not the standard
definition).
2. The perimeter of a polygon is the sum of the lengths of all the sides of the polygon.
3. We define the exterior angles of a polygon as the angles obtained by extending one side (either) at
all vertices.
CHAPTER 1. THINGS YOU SHOULD KNOW
6
"
#
!
$
%
&
Figure 1.5: α, β, γ, δ, and φ are external angles
Cool Fact 9 The sum of the interior angles of a polygon with n sides equals n · 180o minus the sum
of the exterior angles.
4. The number of diagonals in an n-gon is n(n − 3)/2.
5. An equilateral polygon is a polygon with all sides congruent to each other.
6. An equiangular polygon is a polygon with all interior angles congruent to each other.
7. If a polygon is equilateral and equiangular then the polygon is regular.
8. A regular polygon possesses a point C (called the center of the polygon) that is equidistant from all
vertices of the polygon. The distance r is called the radius of the polygon.
!
C
r
Figure 1.6: A regular polygon with center C, radius r, and apothem ρ
The height of the triangles formed by using the center is called the apothem of the polygon (denoted
ρ or just a).
Cool Fact 10 The apothem is the radius of the circle inscribed in the polygon, this circle touches each
side of the polygon at its midpoint.
Cool Fact 11 The area A of a regular polygon can be computed by using its apothem a and its perimeter P . In fact
a·P
A=
2
Cool Fact 12 Using the picture above, of a regular polygon partitioned into congruent triangles, we
could find the sum of the interior angles of the polygon. This idea may be generalized to any polygon
Cool Fact 13 The measure of an interior (or exterior) angle of a regular polygon can be computed by
just knowing the number of sides of the polygon.
Cool Fact 14 If α is half of an interior angle of a regular polygon and s is half the length of a side
of the polygon, then the apothem a is given by
a = s tan α
CHAPTER 1. THINGS YOU SHOULD KNOW
7
9. Two polygons are said to be similar (symbol ∼) if there is a one-to-one correspondence between their
vertices such that all pairs of corresponding angle are congruent and the ratios of of the measures of
all pairs of corresponding sides are equal.
In the following picture 4ABC ∼ 4P QR but 4ABC 6∼ 4RP Q
C
Q
B
A
R
P
Figure 1.7: Similar triangles
Cool Fact 15 Any two regular polygons with the same number of sides are similar.
Cool Fact 16 The apothems of two similar regular polygons are in the same ratio as their corresponding sides.
1. A triangle is a polygon with exactly three sides. Depending on the picture one can determine its base
C
B
A
Figure 1.8: Triangle with base AB
The angles ∠CAB and ∠ABC are called base angles.
2. A triangle with at least two sides congruent is called an isosceles triangle. For instance, the following
picture represents an isosceles triangle as long as AC ∼
= BC.
C
B
A
Figure 1.9: Isosceles triangle
Cool Fact 17 The base angles of an isosceles triangle are congruent. And, conversely, a triangle
having congruent base angles is isosceles.
3. A triangle with all three sides congruent is called an equilateral triangle.
Cool Fact 18 An equilateral triangle is equiangular. That is, and equilateral triangle is regular.
CHAPTER 1. THINGS YOU SHOULD KNOW
8
4. A triangle with a right angle is called a right triangle. The two sides that form the right angle are
called arms or legs of the triangle, the third side is called the hypothenuse.
Cool Fact 19 (Pythagorean theorem) In a right triangle with legs measuring a and b and hypothenuse
measuring c, it is always true that a2 + b2 = c2
5. A triangle with one obtuse angle is called an obtuse triangle.
6. A triangle with three acute angles is called an acute triangle.
7. A median of a triangle is a segment from a vertex to a midpoint of its opposite side.
8. An altitude of a triangle is a segment starting at a vertex and ending at the point it intersects the line
containing the opposite side. Altitudes are always perpendicular to the line containing the opposite
side.
9. The segment that joins the midpoints of two sides of a triangle is called a midline of the triangle.
Cool Fact 20 A midline’s length is one half of the length of the third side of the triangle. Also, a
midline is parallel to the third side. That is, in the following picture the length of AC is twice the
length of EF , and AC||EF .
C
E
A
F
B
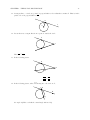
10. The perpendicular bisectors of a triangle are the three perpendicular bisectors of the sides of the
triangle.
Cool Fact 21 The perpendicular bisectors are concurrent, the intersection point (called the circumcenter) is the center of the circle circumscribed to the triangle.
B
C
O
A
Figure 1.10: O is the circumcenter of 4ABC
11. The angle bisectors of a triangle are the three bisectors of the angles of the triangle.
Cool Fact 22 The angle bisectors are concurrent, the intersection point (called the incenter) is the
center of the circle inscribed to the triangle
CHAPTER 1. THINGS YOU SHOULD KNOW
9
C
B
P
A
Figure 1.11: P is the incenter of 4ABC
12. The area of a triangle with base b and altitude h is A(4) =
bh
.
2
Cool Fact 23 The area of a triangle with sides with length a, b, and c is given by
A(4) =
p
s(s − a)(s − b)(s − c)
where
s=
a+b+c
2
This is called Heron’s formula.
13. In any triangle the sum of the lengths of any two sides is greater than the remaining one. This is the
triangle inequality!!
14. In any triangle the angle opposite the greater side is greater, and vice-versa.
15. If two triangles have two sides congruent to two sides respectively, and have the angle contained by
the congruent sides congruent, then the triangles are congruent (SAS)
16. If a triangles has its three sides congruent to the sides of a second triangle, then the triangles are
congruent (SSS)
17. If two triangles have two angles congruent to two angles respectively, and one side equal to one side,
namely, either the side adjoining the equal angles, or that opposite one of the equal angles, then the
triangles are congruent. Note that is a little more than just ASA
18. We have already learned the definition of similarity of polygons, now we will see what happens with
similar triangles. We have two main criteria for similarity.
i If two triangles have two pairs of corresponding angles that are congruent, then they are similar.
ii If two corresponding sides are in the same ratio and the angles they form (in each triangle) are
congruent, then the triangles are similar.
Cool Fact 24 The triangle formed by the midlines of a triangle is similar to the original triangle.
C
B’
A’
A
C’
B
Figure 1.12: 4ABC ∼ 4A0 B 0 C 0
CHAPTER 1. THINGS YOU SHOULD KNOW
10
Cool Fact 25 The ‘triangle inside another triangle’ and the ‘bowtie‘ figure are classical cases of triangle similarity. In fact, if
C
E
B
D
A
where AB||DE, then 4ABC ∼ 4DEC. And if
C
E
B
D
A
where AC||DE, then 4ABC ∼ 4EBD.
19. (Thales’s theorem) Let 4ABC be the right triangle in the picture below
C
h
A
p
D
q
B
where h is the height, p is the length of AD and q is the length of DB. Then, h2 = pq.
20. The sum of the interior angles of a triangle is 180o .
21. A polygon with 4 vertices (and sides) is called a quadrilateral.
22. Two sides of a quadrilateral that have a common vertex are called adjacent sides and two sides that
do not have a common vertex are called opposite sides.
23. The diagonals of a quadrilateral are the segments that are not sides of the quadrilateral whose
endpoints are vertices of the quadrilateral.
24. A parallelogram is a quadrilateral whose opposite sides are parallel.
25. Two angles that have their vertices at the endpoints of the same side of a parallelogram are called
consecutive angles.
26. An altitude of a parallelogram is a segment that is perpendicular to two opposite sides (or the lines
that contain them).
27. The area of a parallelogram with altitude measuring h and base b is A = bh.
28. A rectangle is a parallelogram with all interior angles measuring 90o .
CHAPTER 1. THINGS YOU SHOULD KNOW
11
Cool Fact 26 The diagonals of a rectangle are congruent. The converse is also true, i.e. if a parallelogram has congruent diagonals, then it must be a rectangle.
Cool Fact 27 It is in the definition that the interior angles of a rectangle are right, but it is also true
that if a quadrilateral has four right angles then it must be a rectangle.
29. A rhombus is a quadrilateral with four congruent sides.
Cool Fact 28 The diagonals of a rhombus are perpendicular to each other. Moreover, they are angle
bisectors.
The converses of these two (individual) facts are also true but only when the quadrilateral is already a
parallelogram. In fact, for a parallelogram to be a rhombus it is enough that one diagonal is a bisector.
Now look at the figure below, in it we see that the diagonal DB is a bisector and that the two diagonals
intersect in 90o , however ABCD is not a rhombus, as their sides are not congruent.
D
A
C
B
Figure 1.13: Nope, not a rhombus
30. The area of a rhombus is given by
A=
d1 d2
2
where d1 and d2 are the lengths of the diagonals.
31. A square is a quadrilateral that is both a rhombus and a rectangle.
Cool Fact 29 If a rhombus has one right angle, then it is a square.
Cool Fact 30 Since a square is a rhombus, then we can compute its area using its diagonals.
32. A trapezoid is a quadrilateral with only two sides parallel. The two parallel sides of a trapezoid are
called bases (sometimes I will call one the base and the other the summit).
33. The two angles adjacent to the base are called base angles, the two angles adjacent to the summit
are called summit angles.
Cool Fact 31 Two consecutive angles in a trapezoid, not both base or summit angles, are suplementary.
34. The median of a trapezoid is the segment joining the midpoints of the two non-parallel sides.
Cool Fact 32 The median is parallel to the bases and it measures exactly
b1 + b2
2
CHAPTER 1. THINGS YOU SHOULD KNOW
12
35. An altitude of a trapezoid is a segment that is perpendicular to both bases (or to the lines containing
them).
36. The area of a trapezoid is given by
h(b1 + b2 )
2
where h is the length of the altitude, and b1 and b2 represent the two bases.
A=
Cool Fact 33 If m is the length of the median of a trapezoid with height h, then we can say that the
area of a trapezoid is A = mh.
37. An isosceles trapezoid is a trapezoid whose non-parallel sides are congruent.
Cool Fact 34 In an isosceles trapezoid the two base angles are congruent, and so are the two summit
angles.
Cool Fact 35 The diagonals of an isosceles trapezoid are congruent.
Cool Fact 36 Any two opposite angles in an isosceles trapezoid are supplementary.
In case you are like me and forget so many properties about trapezoids, just keep in mind the following
picture.
Figure 1.14: An ‘extended’ trapezoid
which shows how a trapezoid can be ‘extended’ to a triangle, and since the bases of the trapezoid are
parallel, then the big triangle is similar to the small (dashed) one... pretty much all you need to know can
be obtained by from this picture.
Circles
1. A circle is the set of all points that are at the same distance r from a given point C. The number r is
called the radius of the circle and C is the center. The largest distance between two points on a circle
is d = 2r, which is called the diameter of the circle.
It is possible to draw a circle with any given center and radius.
Cool Fact 37 Two circles intersect in at most two points.
2. A line intersects a circle C in at most two points. A line that does not intersect C is said to be exterior,
a line that intersects C in exactly one point is a tangent, and a line intersecting C is called a secant.
3. The segment, created by a secant line, that is between two points of the circle is called a chord.
Cool Fact 38 If a chord is perpendicular to a radius, then the radius bisects the chord
CHAPTER 1. THINGS YOU SHOULD KNOW
13
Cool Fact 39 If two chords are at the same distance from the center then they are congruent.
4. Let us recall that there is a second way to measure angles, by using radians. We use radians when
we want to use length (inches, yards, centimeters, etc) to measure angles. The conversion rate from
degrees to radians is given by 180o = π radians.
5. An angle with vertex at the center of the circle is called a central angle. An angle with vertex at a
point of the circle is called an inscribed angle.
D
"
E
#
B
C
!
A
Figure 1.15: α is central, β and γ are inscribed
Cool Fact 40 Note that the angles in the picture above share points A and B, when this happens we
get that the central angle is exactly twice the inscribed angle. That is,
2γ = 2β = α
Cool Fact 41 Using the previous cool fact we can see that any triangle inscribed in a circle with the
diameter as a base must be a right angle. That is, if in the picture below DB is a diameter then both
4DBC and 4DBA are right.
C
D
B
A
Cool Fact 42 Any pair of opposite angles in a quadrilateral inscribed in a circle are supplementary.
That is, in the picture below ∠D + ∠B = ∠C + ∠A = 180o .
C
D
B
A
Figure 1.16: Quadrilateral inscribed in a circle
CHAPTER 1. THINGS YOU SHOULD KNOW
14
6. The points on a circle that lie between the two points a central angle intersects the circle is called a
circle arc. The whole ‘slice’ obtained by drawing a central angle is called a circle section.
In the picture below, the shaded area is the section associated to the same center angle as the blue arc.
7. The perimeter (or circumference) of a circle with radius r is P = 2πr. The area of a circle is A = πr2 .
Cool Fact 43 The length of a circular arc with central angle α (in radians) is `α = αr. The area
2
of a circle sector with central angles α is Aα = αr2 .
It follows that congruent central angles yield congruent arcs and sectors.
8. In the picture below, α equals one-half of the sum of the central angles that are determined by the
arcs AB and CD.
C
B
!
A
D
9. In the picture below, α equals one-half of the difference of the central angles that are determined by
the arcs AB and CD.
B
C
!
D
A
10. In the picture below,
BE · ED = AE · EC
C
B
E
A
D
(note that I am talking about the multiplication of the lengths of those segments)
CHAPTER 1. THINGS YOU SHOULD KNOW
15
11. A tangent line to a circle at a point P is perpendicular to the radius that contains P . That is, in the
picture below l is perpendicular to CP .
P
r
l
C
12. Let us throw two tangent lines from a point A outside the circle
P
A
Q
Then AP ∼
= AQ
13. In the following picture
P
A
R
Q
AQ
AP
=
AP
AR
←→
14. In the following picture, where P R is tangent to the circle at P ,
P
R
Q
the angle ∠QP R is one-half the central angle with arc P Q.
CHAPTER 1. THINGS YOU SHOULD KNOW
16
3 − D geometry
1. Let us called E3 to our three-dimensional space. E3 is formed by points, lines, planes and many other
curves and solids.
2. Two distinct lines in E3 can be skew (no intersection and pointing in different directions), parallel (no
intersection and pointing in the same direction), or they intersect in a point.
3. Just as an infinite number of points create a line, an infinite number of lines create a plane, which only
has two dimensions (width and length).
Cool Fact 44 If two distinct planes in E3 intersect, then they do so along a line. Also, two distinct
planes could be parallel (meaning no intersection).
4. A prism is a solid with parallel congruent bases (most of the times polygons)
Figure 1.17: Prisms
A prism with bases that are not aligned one directly above the other is called an oblique prism.
Figure 1.18: Oblique prism
Cool Fact 45 A prism with a polygonal base has parallelograms as lateral faces.
5. The surface area of a solid is the sum of the areas of all its faces. The volume of a solid measures the
amount of space it occupies in space. Here is a list of formulas for surface area and volume:
Volume
Surface area
Prism
Cone
Pyramid
h · Abase
1
2
3 hπr
1
3h
h · Pbase + 2Abase
πrs + πr2
where
(a)
(b)
(c)
(d)
(e)
Abase is the area of the base of the solid,
Pbase is the perimeter of the base of the solid,
h is the height of the solid,
r is the radius of the circle that is the base of the cone,
R is the radius of the sphere
· Abase
? see below
Sphere
4
3
3 πR
4πR2
CHAPTER 1. THINGS YOU SHOULD KNOW
17
(f) s is the length of the slant height of a cone
s
Figure 1.19: Cone with slant height s
? The surface area of the pyramid depends on the number of sides, and the shape, of the polygon used
for the base.
The Cartesian plane and conics
We can write every point P on the plane as a unique ordered pair of numbers P = (x, y). The numbers x
and y are called the coordinates of P . This presentation of the plane as a set of ordered pairs is called the
Cartesian plane.
Given two points P = (x1 , y1 ) and Q = (x2 , y2 ) then we can find the distance between P and Q by using
the formula
p
d(P, Q) = (x2 − x1 )2 + (y2 − y1 )2
The conic sections are obtained as intersections of a double cone with a plane, like in the picture below
Ellipse
Hyperbola
Parabola
Figure 1.20: The conic sections
The intersections are of three types; ellipses, hyperbolas or parabolas. A circle is a type of ellipse (look
at the base of the cone).
We want to study these curves in a coordinate plane so we can find their equations.
1. A circle with center (h, k) and radius r has equation.
(x − h)2 + (y − k)2 = r2
CHAPTER 1. THINGS YOU SHOULD KNOW
18
2. The equation of the ellipse
b
(h,k)
a
a
b
is
(y − k)2
(x − h)2
+
=1
2
a
b2
3. The equation of the hyperbola
2a
(h,k)
2b
is
(y − k)2
(x − h)2
−
=1
a2
b2
CHAPTER 1. THINGS YOU SHOULD KNOW
19
Exercises
1. Show cool facts 2, 3, and 6.
2. Show the vertical angle theorem.
3. The sum of the interior angles of a polygon with n sides equals n · 180o minus the sum of the exterior
angles.
4. Show cool fact 9.
5. Show cool fact 11.
6. What is the measure of an interior angle of a regular n-gon. Repeat with an external angle.
7. What is the sum of the interior angles of a convex polygon. What is the sum of the exterior angles?
Hint: You may want to consider the pictures below
8. Show cool facts 15 and 16.
9. Show cool fact 21 and 22
10. Show cool fact 23.
11. Show cool facts 24 and 25.
12. Show Thales’s theorem.
Hint: Use similarity of triangles.
13. Use Thales’s theorem to show that if p, q > 0 then
the arithmetic mean).
√
pq ≤ (p + q)/2 (the geometric mean is at most
14. Show cool fact 26.
15. Show that if a quadrilateral has diagonals that are perpendicular to each other and angle bisectors,
then the quadrilateral must be a rhombus.
16. Show that the area of a rhombus is A =
d1 d2
, where d1 and d2 are the lengths of the diagonals.
2
17. Show cool fact 29.
18. Show cool facts 31 and 32.
19. Show that the area of a trapezoid is A =
b2 represent the two bases.
20. Show cool facts 34, 35, and 36.
21. Show cool facts 38 and 39.
h(b1 + b2 )
, where h is the length of the altitude, and b1 and
2
CHAPTER 1. THINGS YOU SHOULD KNOW
20
22. Show cool facts 40 and 42.
23. Show items 8, 9 and 10 in page 13.
24. Show items 12, 13 and 14 in page 14.
25. Prove the formulas for surface area in the table given in the 3 − D geometry section for the cone, prism,
and pyramid with any polygonal base.
26. The trapezoid RW T S is isosceles
S
T
P
W
R
Is 4RP W isosceles?
27. Let LM be the median of the trapezoid ABCD, and P the midpoint of AD
B
C
L
M
A
D
P
If LP ∼
= M P . Show that ABCD is isosceles.
28. If α > β. Can ABCD be a rectangle?
D
C
E
A
"
!
B
29. Let #ABCD be a parallelogram, AE ∼
= CF ,
B
!
C
F
E
A
D
Find ∠CDF .
30. If the edge of a cube is y. What is the distance from one corner of the cube to the furthest corner on
the opposite side of the cube?
31. Consider a cone that has been cut/sliced by a plane that is parallel to its base, like in the picture below
CHAPTER 1. THINGS YOU SHOULD KNOW
21
If the height of the cone is h, the height of the little cone that is formed above the highest plane is k,
the slant height of the big cone is p + q and the slant height of the little cone is p, then what is the
ratio of the surface areas of the cones?
32. Using the picture below
C
l1
#
!
A
"
l2
B
where l1 ||l2 . Show that the sum of the interior angles of 4ABC is 180o .
33. Consider a right triangle with hypothenuse c and legs a and b. Now take four copies of it and arrange
them in a square in the following way
b
a
a
c
c
b
b
c
c
a
a
b
Conclude the Pythagorean theorem.
Now with the same right triangle used above, use the following figure to find a different proof for the
Pythagorean theorem.
c
b
a
c
a
b
b
b
a
c
a
c
34. Assume that ABC, ACE, and CDE are semicircles, and that AC ∼
= CE. Show that the area of the
shaded region is equal to the area of 4ACE
CHAPTER 1. THINGS YOU SHOULD KNOW
22
C
B
D
E
A
35. Consider the following figure
which is obtained by drawing a square inscribed in a circle and then four semicircles with diameters
the sides of the square.
Show that the red area is equal to the blue area.
36. Assume that CXEY is a square, where C is the center of the circle. Show that the arc QP is congruent
to the arc JT .
T
P
E
Y
X
C
Q
J
37. Assume that ∠ACE = 30o , AF ||BE, and AB||ED.
F
A
B
C
E
D
Find ∠F AB
38. Consider a ‘sand-clock-like’ figure formed by two congruent cones sharing their vertex. This figure
is perfectly fit inside a cylinder that has the same base as the cones’... something like the following
picture.
CHAPTER 1. THINGS YOU SHOULD KNOW
23
If the radius of the base is 3 in and the height of the cylinder is 8 in. What portion of the volume of
cylinder is the volume of the sand clock?
Chapter 2
Measuring is overrated
A.K.A Size does not matter
Many of the properties we know in geometry use the idea of measure. For instance, a circle needs the idea
of distance to be defined, something similar happens when we measure angles, areas, volumes, etc. In this
chapter we will see how far we can get without using any type of measure, thus we will play with objects
like points, lines, planes, etc.
When one wants to define what a (straight) line is, most of the times, one tends to go in circles:
• A line goes straight.... something goes straight when it follows a line
• A line does not bend... bending is when one goes out of a straight path...
This becomes more and more complex when ideas such as “the shortest distance between two points is
given by a line” are matched with what happens in a sphere, cone, saddle... over there lines are not that
straight anymore! Thus we need to forget about our intuition and the idea of measure to capture the essence
of what a line is.
1. Any line has at least two points,
2. Any two points are in at most one line.
This is too simple, as figures like the following three
are not what we would call a geometry by do satisfy the previous two properties. Let us try again, now we
follow Euclid
1. Any two points determine a unique line,
2. For an given line ` and point P ∈
/ ` there is a unique line that goes through P and is parallel to `.
This one does not quite work either as a space containing a line having a single point will satisfy the
previous properties but it is not what we want. So, we want our lines to have at least two points.
How far can we get with these properties? Not too far, as property two needs of a line ` and point P ∈
/`
for it to work, and not having the proper conditions may lead to a degenerate geometry. For instance, a
line formed by two points (and nothing else, no more lines, no more points) satisfies both properties.. but
24
CHAPTER 2. MEASURING IS OVERRATED
A.K.A SIZE DOES NOT MATTER
25
it looks nothing like what we are used to think when we do geometry. Thus we will need to add a third
property to assure things are not too strange.
Euclid has also another ‘rule’ for lines, that one can extend a segment into an infinite line, but in our
case (no measure) what does it mean to extend a line? To make something longer is an idea belonging to
measure-world. So, we will not consider it for now.
Affine planes
Define an affine plane Π as a set of points P and a set of sets of points (lines) L such that
1. Any two points determine a unique line (which forces that any two distinct lines intersect in at most
one point),
2. Lines contain at least two points.
3. For an given line ` and point P ∈
/ ` there is a unique line that goes through P and is parallel to `,
4. There are three points not on a line.
Note that in this definition we have stripped lines off of their ‘straight’ property we are so used to. So,
it shouldn’t be so surprising to have lines that are weird-looking.
Definition 1 An affine plane is said to be finite if it contains finitely many points. It is called infinite
otherwise.
Example 1 The smallest possible affine plane has 4 points and 6 lines, it can be represented as
Figure 2.1: AG(2, 2)
This plane is called the affine plane of order 2 or just AG(2, 2), where AG stands for ‘affine geometry’,
the first 2 is because a plane is 2 dimensional, and the second 2 is because lines have 2 points.
One way to look at geometry, specifically when working with lines and points, is by using coordinates.
In the Euclidean/Cartesian plane lines look like y = mx + b, where m, b ∈ R. That is, lines are just parallel
translations of lines that go through the origin, i.e. the line y = mx + b is a parallel translation of y = mx.
Can we mimic this in AG(2, 2)?
Since AG(2, 2) looks like a square then we can take the base and left side as the x-axis and y-axis
respectively, this also sets our origin. Of course, we will not have many points in our axes but that is OK.
We now note that there are three lines through the origin, as mentioned before two of them are the axes, or
x = 0 and y = 0, the third one goes through the origin and the intersection of two lines that are parallel to
the axes. By labeling a few points (see figure below) we get that the third line goes through (0, 0) and (1, 1),
and thus it is y = x. The last line to label should be a translate of y = x... copying that the translations
used in the other lines were done by a ‘+1’, let us say the third line is y = x + 1. We get,
CHAPTER 2. MEASURING IS OVERRATED
1
A.K.A SIZE DOES NOT MATTER
26
y=1
y=x
x=0
x=1
y=x+1
y=0
1
Figure 2.2: AG(2, 2) with coordinates
How can we rig this to get the last line to be y = x + 1? We want the points (1, 0) and (0, 1) to be in
that line. By plugging these points into y = x + 1 we realize that we need 0 = 1 + 1. Now it all makes sense,
as the coordinates for the points were 0’s and 1’s and now we need 0 = 1 + 1. It follows that we are using
Z2 to coordinatize AG(2, 2).
Definition 2 The set S of lines through the origin in an affine plane that is necessary to obtain all lines in
the plane as translates of elements in S is called a spread of the plane.
Remark 1 Not every affine plane possesses a spread.
Example 2 The set of lines S = {x = 0, y = 0, y = x} is a spread of AG(2, 2).
Example 3 The next affine plane (in terms of number of points it contains) is AG(2, 3).
Figure 2.3: AG(2, 3)
When we coordinatize this plane we notice that we have three points per line, and thus we will need to
use 0, 1 and 2 for coordinates. A spread for AG(2, 3) is given by S = {x = 0, y = 0, y = x, y = 2x}, and
that the operations need to be done in Z3 for all this to work.
Definition 3 The affine plane of order n that is coordinatized by a field with n elements is called AG(2, n).
Remark 2 Not all affine planes are AG(2, n)’s.
In the previous examples we have seen that all lines in an affine plane have the same number of elements,
also that the number of lines through a point stays constant, and that the number of lines and points are
almost the same. This is not a coincidence.
Theorem 1 Let Π be a finite affine plane, then there is a positive integer n, called the order of Π, such that
every line has exactly n points and every point is in exactly n + 1 lines.
CHAPTER 2. MEASURING IS OVERRATED
A.K.A SIZE DOES NOT MATTER
27
Proof. Assume there is a line l with n points, and let P be any point not on l. Then we can draw n distinct
(why distinct?) lines P Q where Q ∈ l, but using axiom 3 in the definition of affine plane we get an n + 1-st
line. Note that every point R ∈ Π must be in one of these lines (why?). Now take l, a line m intersecting
l and a point P ∈
/ l ∪ m (why does this point exist?). If we count the lines through P using the same idea
used in the previous paragraph, but now using m instead of l, we will get that the number of points in m is
equal to the number of points in l. It follows that all lines have the same number of points and that a point
in l is in exactly n + 1 lines (why?).
Corollary 1 An affine plane of order n contains n2 points and n2 + n lines. Also, every maximal set of
parallel lines contains exactly n lines, and thus a spread of such a plane (if it exists) contains n + 1 lines.
Something interesting happening here is that we can add a new ‘line’ to an affine plane to create a new
type of plane, one that will keep most of the main properties of an affine plane except for the one about
parallel lines. In fact, there will not be parallel lines in this plane.
Consider an affine plane π of order n. Partition the lines into bunches of mutually parallel lines, corollary
1 says that there are n + 1 classes each containing exactly n lines. Next we label each classes with some
index, a ‘slope’ if you please, from {m1 , m2 , · · · , mn+1 }. Since we want to keep the main properties of an
affine plane, then we cannot create new intersections but only among parallel lines, so we will say that all
lines in the class with slope mi will intersect at a new point called (mi ). This will create n + 1 new points,
which we will say determine a line that we will call `∞ .
The object created from an affine plane of order n by adding `∞ will be called a projective plane of order
n (in particular, from AG(2, n) we obtain P G(2, n)). An easy counting argument shows that a projective
plane of order n contains n2 + n + 1 lines, n2 + n + 1 points, and that every point is in exactly n + 1 lines
and every line contains n + 1 points. Much more symmetric now!!! Also, we can define a projective plane in
a general way by just modifying the definition of an affine plane.
Projective planes
A projective plane Π is a set of points P and a set of sets of points (lines) L such that
1. Any two points determine a unique line,
2. Lines contain at least three points,
3. Two distinct lines intersect in one point,
4. There are four points not three of them on a line.
Example 4 We use the picture we have of AG(2, 2) to construct P G(2, 2).
1
y=1
y=x
x=0
x=1
y=x+1
y=0
1
where the three red points are the new points, on the new line `∞ . However, the picture is very awkward, so
we will re-draw it (keeping the color code) as what is called the Fano plane.
CHAPTER 2. MEASURING IS OVERRATED
A.K.A SIZE DOES NOT MATTER
28
(0,1)
(1,1)
(0,0)
(1,0)
Figure 2.4: The Fano plane
Sometimes it is not that easy to get a nice picture for a given projective plane, thus we will not be able
to study projective planes by working with pictures. For instance, in the picture below, the first two figures
represent P G(2, 3) and the third represents P G(2, 4)
Figure 2.5: P G(2, 3) and P G(2, 4)
Do not forget that affine planes need not to be finite. In fact, if one takes the Euclidean affine plane and
constructs a projective plane from it then one obtains the real projective plane, which we will study later.
If in a projective plane one calls its points lines and its lines points, and ‘flips’ the sign ∈ accordingly
then one obtains another projective plane, called ‘the dual plane of Π. This re-labeling is called dualization.
We can dualize not only whole planes but also properties, shapes, etc that take place in a projective
plane. For example, the dual property of three lines that are concurrent is three points that are collinear.
Definition 4 Two triangles 4ABC and 4A0 B 0 C 0 are in perspective from a point O if once a correspondence
between the vertices of the triangles has been set (in this case A ↔ A0 , B ↔ B 0 , and C ↔ C 0 ) then the pairs
of corresponding vertices are collinear with O.
O
B
A
C
B’
A’
C’
Figure 2.6: 4ABC and 4A0 B 0 C 0 in perspective from O
CHAPTER 2. MEASURING IS OVERRATED
29
A.K.A SIZE DOES NOT MATTER
We can now attempt to define what it means for 4ABC and 4A0 B 0 C 0 to be in perspective from a line,
we will do this by dualizing definition 4.
Definition 5 Two triangles 4ABC and 4A0 B 0 C 0 are in perspective from a line l if once a correspondence
between the points in the triangles has been set (in this case A ↔ A0 , B ↔ B 0 , and C ↔ C 0 ) then the pairs
of corresponding sides are concurrent with l.
B
A
C
B’
A’
C’
l
Figure 2.7: 4ABC and 4A0 B 0 C 0 in perspective from l
Since in the pictures above we used the same triangles, then it is not so strange to try to put both pictures
together. This arrangement of lines and points is called the Desargues configuration.
O
B
A
C
B’
A’
C’
l
Figure 2.8: Desargues configuration
So, we have that 4ABC and 4A0 B 0 C 0 are in perspective both from a point and from a line. This
situation does occur in many projective planes (in particular in the one constructed from the Euclidean
affine plane and in the P G(2, n)’s) but not in all of them. Surprisingly, the definition of projective plane
leaves things ‘loose’ enough to allow planes with many different characteristics to exist. Anyway, we phrase
now a theorem that we will (hopefully) prove later in the semester.
Theorem 2 (Desargues) In a projective plane arising from an ‘Euclidean’ affine plane. If two triangles
are in perspective from a point, then they are also in perspective from a line.
Cool Fact 46 The converse of the theorem of Desargues is also true, as it is just the dual of itself.
Another very important result of the same type (i.e. valid only in ‘Euclidean’ planes, and that we will
hopefully prove later) is
CHAPTER 2. MEASURING IS OVERRATED
A.K.A SIZE DOES NOT MATTER
30
Theorem 3 (Pappus) If the six vertices of a hexagon lie alternately on two lines, then the three pairs of
opposite sides meet in collinear points.
That is, in the following picture, we start with the hexagon AB 0 CA0 BC 0 and we obtain that the points
P , Q and R are collinear.
A
B
Q
P
A’
B’
C
R
C’
Figure 2.9: Pappus configuration
Remark 3 So far we have seen examples of planes that do not necessarily satisfy the same set of properties,
and that, in spite of this, one can study properties of figures/shapes living in these planes. As properties of
figures must always be proved, the one thing that cannot be left out is that the set of axioms of a plane has
to be consistent, meaning that the axioms cannot contradict themselves.
Hence, it should not be a surprise anymore to talk about geometry even though the properties we are
learning/studying are not ‘the usual ones’ or are counterintuitive. We will see more of this in the next
chapters.
The moral of this remark is that if you think something is true, then you should have a reason to believe
so. Intuition is never enough... prove it.
Other measure-free results in geometry
We know a polyhedron is formed by vertices, edges and faces. Around 1639, Descartes discovered a number
that was the same for all (convex) polyhedra (the total angular defect). His discovery could have been
re-phrased in terms of edges, vertices and faces. Years later, around 1750, Euler re-discovered this formula
in the simpler form we will see next. The first proof for this formula was given by Legendre in 1794.
Theorem 4 (Euler’s formula for polyhedra) Let P be a polyhedron with V vertices, E edges, and F
faces, then V − E + F = 2.
Proof. Consider a polyhedron P, think of it as a rubber sphere with flat sides. Then remove a point from
one of the faces and stretch and flatten the solid to get a planar figure with vertices and edges that connect
them. Note that for any two vertices there is always a path made out of edges that joins them (why?). We
can call this object ‘flat P’.
Figure 2.10: Flat cube
CHAPTER 2. MEASURING IS OVERRATED
A.K.A SIZE DOES NOT MATTER
31
It is easy to see that by extracting an edge from the graph one is not only subtracting one edge but also
a face, thus the Euler’s formula of the new figure is equal to the previous figure’s. If one keeps going this
way then one gets to the point where the figure has been transformed into a polygon (why?), which has the
same Euler’s formula as P (why?).
We now recall that the exterior of our polygon was a face of P, then we can compute the Euler’s formula
of this polynomial, we get V − E + F = 2.
We will now use this theorem to find out how many regular polyhedra there are.
Definition 6 A polyhedron is said to be regular if its faces are congruent regular polygons and that has the
same number of faces meeting at each vertex. A convex regular polyhedron is called a Platonic solid.
Corollary 2 There are only five Platonic solids. They are:
Figure 2.11: The five Platonic solids
Proof. Let P be a Platonic solid, then each vertex has the same number of edges branching from it, call
this number d. Also, each face has the same number of sides (edges), call this number k.
We know that each edge touches two vertices and that each vertex touches d vertices. Then, by counting
the number of pairs (e, v) where e is an edge and v is a vertex we get:
2E = V d
Similarly, since each edge separates two faces, then
F k = 2E
By plugging these values into the Euler formula for P we get:
2E
2E
2
2
−E+
=2
or
E
−1+
=2
d
k
d
k
We note that, since E > 0 then d2 − 1 + k2 > 0 or, in other words, d2 + k2 > 1. Since we need at least
three sides per face then k ≥ 3. Similarly, d ≥ 3 (why?). Now we see that if any d or k are larger than 5
then there is no way that the inequality holds (why?). Thus d and k can be 3, 4, 5.
By just trying numbers we get that the solutions for the inequality are:
(d, k) = (3, 3), (3, 4), (4, 3), (3, 5), (5, 3)
These pairs yield:
CHAPTER 2. MEASURING IS OVERRATED
(d,k)
(3, 3)
(3, 4)
(4, 3)
(3, 5)
(5, 3)
V
4
12
6
20
15
E
6
8
12
30
30
A.K.A SIZE DOES NOT MATTER
F
4
6
8
12
20
32
Name
Tetrahedron
Cube
Octahedron
Dodecahedron
Icosahedron
Another corollary of the Euler’s formula is Pick’s theorem. We will not prove this one because it requires
knowledge of algebra.
Theorem 5 (Pick) The area of a (not necessarily convex) polygon Q with vertices having both coordinates
in Z (the vertices are integral points) is given by
1
A(Q) = nint + nbd − 1
2
where:
nint = number of integral points in the interior of Q
nbd = number of integral points in the boundary of Q.
Example 5 For the following polygon P
we get nint = 5 and nbd = 13. Then, using Pick’s theorem we get that its area is 5 + 13
2 − 1 = 10.5. By
re-arranging pieces of the polygon one can check that the area of the polygon is actually 10.5 (square units).
CHAPTER 2. MEASURING IS OVERRATED
A.K.A SIZE DOES NOT MATTER
33
Exercises
1. Give an example of an infinite affine plane.
2. Finish the details in example 3 then construct AG(2, 5) (a picture would be nice but it might be pretty
ugly). Be sure of explaining how the coordinatizations work, and why Z3 and Z5 are the fields that
are necessary for everything to work out alright.
3. Fill the gaps in the proof of theorem 1.
4. Prove corollary 1.
5. Suppose you have 4-dimensional vector space V over Zp , p prime, and a set of 2-dimensional subspaces
that cover the points of V and that pairwise intersect at the zero vector. Show that taking translates
of the subspaces creates lines that when put all together define an affine plane. What would be the
order of the plane?
Such planes are called translation planes.
6. Do the counting that shows how many points per line, how many lines per point, how many points
and lines there are in a projective plane of order n.
7. Show that we can partition the set of all lines of an affine plane of order n into (disjoint) sets by putting
all lines that are parallel to each other in the same set (these sets are called parallel classes). Also,
show that all these sets have the same number of elements.
8. Show that the relation on the set of lines of an affine plane defined by l ∼ m if and only if l is parallel
to m defines an equivalence relation and thus the parallel classes described in the previous problem are
just equivalence classes under this relation.
9. Show that the construction of a projective plane from an affine plane satisfies the 4 axioms in the
definition of projective plane. Also, show that a projective plane minus a line and all the points on it
yields an affine plane.
Hint: For the second part you might want to use the results in problem 6.
10. Take the standard Euclidean plane and then elaborate on what ‘real life’ situations might be explained
by considering a projective plane instead of an Euclidean plane.
11. Convince yourself that the two pictures in figure 2.3 representing AG(2, 3) are, in fact, just different
pictures of the same plane.
12. What is dual picture of a triangle? Repeat replacing triangle with quadrilateral, pentagon, and
hexagon.
13. Find the dual of the dual of the following picture
14. Show that by dualizing a projective plane one obtains a projective plane. Now assume that the original
plane has order n, what is the order of its dual?
15. Show that the dual of a finite affine plane is not an affine plane.
CHAPTER 2. MEASURING IS OVERRATED
A.K.A SIZE DOES NOT MATTER
34
16. Find a Desarguesian configuration (figure 2.7) and a Pappus configuration (figure 2.9) in P G(2, 3)
(figure 2.5).
17. Show that the dual of the theorem of Desargues is its converse.
18. What is the dual of the theorem of Pappus?
19. Fill the gaps in the proof of Euler’s formula.
20. Fill the gaps in the proof of the existence of exactly five Platonic solids.
Chapter 3
Cylinders, cones, spheres, etc.
In this chapter we will explore the geometry of spaces that are not the usual Euclidean plane. In order to
do that we will need to first understand what defines the main objects we use in standard geometry. The
good thing is that now we will be able to use distances, and thus angles, for our study.
The first goal is to define lines (straight lines, that is). Since the spaces we want to investigate are
contained in the three-dimensional space we live in, then it would be plausible to think that these spaces
will inherit lines, circles, etc from their ambience space. But, does that even make sense?
Think of the sphere, and match it with our planet Earth. Now consider a straight line in space... does
that constitute a straight line on Earth? Not really. Thus, when we want to study lines, circles, etc on a
space such as the sphere we need to embed ourselves into it, we need to think as if we lived on the surface
of the sphere (or cone, cylinder, etc). We have to think locally, not globally.
The difference between local and global (or intrinsic and extrinsic) is clearly seen in a Möbius band and
a cylinder. A Möbius band is obtained by taking a strip of paper and twisting once before gluing the ends.
Figure 3.1: Möbius band
Of course, a cylinder is obtained from the same strip of paper but gluing the ends without any twisting.
It is clear that if one is standing at a point ‘in the middle’ of the band (see picture below) or ‘in the
middle’ of a cylinder, then a line (locally) would go parallel to the edge(s) of each space.
P
However, globally, the line on the cylinder will always stay on the outside of it, but on the band the line
will go and pass to the other side of it.
Since we live on a sphere (well, almost) it is probably easier for us to study the basics of spherical
geometry first. This is a good starting point.
35
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
36
The sphere
It is not so hard to convince oneself that if one wanted to go ‘straight’ on the surface of Earth from a point
on the equator to another point in the equator, then the way to go would be to follow the equator. Now, if
we wanted to go straight from any point P to any point Q on the sphere, then we can always rotate a sphere
so that both points lye on the new equator (after rotations have been made). It follows that straight lines
on the sphere are given by ‘equators’, they are actually called great circles.
Another argument for lines on the sphere being great circles is more empirical. Take a sharpie and any
spherical object. Take two points P and Q on the sphere and draw, with the sharpie, what seems to be the
‘straightest’ way to get from one to the other, once you have done this extend this line around the sphere,
you will see that you will get a great circle containing P and Q.
Yet another experiment one can design with any spherical object requires a piece of string (or something
similar). First position the string on the two points and then pull on one side (creating the shortest possible
path between P and Q). Then again you will see that the string will use the same path you drew with the
sharpie.
A similar experiment is to take a point and with a sharpie draw a ‘direction’ on the surface of the sphere,
if you prolong this direction you should get around and reach the point you started with again, on the way
you would have created a great circle.
More ways to convince ourselves about great circles being lines on a sphere comes from analyzing regular
lines on the Euclidean plane, as these lines have very important symmetry properties. For example, we can
reflect the whole plane across the line and we will get the same plane back, meaning that what is ‘above’ the
line is, in some sense, equal to what is ‘below’ it (in particular, the line is fixed under this reflection). If we
take any curve on the sphere that is not a great circle then we will see clearly that the two halves created by
the curve will not be equal. Similarly, in the Euclidean plane if P is a point on a line `, then we can rotate
the whole plane around P half a revolution (180o ) and get the ‘same’ plane back (in particular, the line is
fixed under this rotation). Trying to repeat this on the sphere with anything but a great circle would fail
miserably. Also, if one moves a point along a line in the Euclidean plane one still has the same plane back,
this does not occur on the sphere unless the point moves along a great circle (note that this movement is a
rotation on the sphere!).
Finally, we are very used to the idea of a line determining the shortest path between two given points. We
mentioned this already above, but now (as an exercise) you will show it. You may need a proper definition
of a great circle.
Definition 7 (Euclid) A small circle on a sphere is obtained by intersecting the sphere with a plane that
does not go through the center of the sphere. When the plane contains the center of the sphere, then the
intersection is a great circle.
So, what is this ‘shortest distance’ thing?
Definition 8 A surface S is a geometric figure (space) that when one looks at the immediate surroundings
of any point P ∈ S one does not see any difference from the surroundings of a point on the Euclidean plane.
A sphere is a surface, as we (living on one) do not see any difference between it and a plane. Similarly,
an infinite cylinder is a surface. Same with an infinite cone, as it is clear that the definition of surface works
well at every point of the cone that is not the vertex. At the vertex we need to look at it from above, then it
is not so hard to see that the surroundings of the vertex also look like a piece of Euclidean plane. However,
that vertex is too sharp, so the cone will not be considered to be smooth.
Another surface we will study a little is the torus, which can be thought of as the surface of a donut.
Figure 3.2: Torus
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
37
An example of a space that is not a surface would be a finite cylinder, because a boundary point on it will
not have surroundings looking like the plane’s. A double cone would also be an example of a non-surface, as
now the vertex has two cones coming out of it, this is not something that happens on the Euclidean plane.
Definition 9 A curve on a surface S that gives the shortest distance between two points is called a geodesic.
Note that a geodesic would determine what is straight in the correspondent surface. As of now we have
convinced ourselves that great circles define geodesics on a sphere, but how do we show there are no other
geodesics we have not been able to see yet? The following theorem takes care of this.
Theorem 6 At every point on a smooth surface (no sharp points) there is a unique geodesic going from that
point in any direction.
Since geodesics would be determined locally (i.e. a point and a direction), then it makes even more
sense to say that geodesics determine what is straight on a surface (recall that straight is something we had
realized should be studied locally).
So, we know what lines are on the sphere. But, do they behave like we expect lines to do? In our
Euclidean experience we have learned that lines intersect in at most a point and that there are parallel lines,
these two properties of lines do not hold for great circles. In fact, two distinct great circles always intersect
in exactly two points, and these two points are antipodal.
Definition 10 Two points on a sphere are called antipodal if the segment (in 3 − D space) joining them
goes through the center of the sphere. For instance, the North and South pole are antipodal.
Note that a sphere with great circles as lines has a ‘projective’ vibe to it, as in a projective plane there
were no parallel lines. However, the fact that lines intersect in more than one point is pretty bad, we will
need to do some surgery there later. For now we will keep studying the sphere with no changes but keeping
in mind that if one looks at a hemisphere then lines will intersect in exactly one point.
Another thing about great circles that is not quite like Euclidean lines is that great circles have a finite
length. This will become important later in certain proofs that need a line to be extended infinitely.
Now that we know what lines are, and we are aware of the differences with standard lines, we can start
thinking about polygons. However, do not forget that polygons do not need to be simple or convex.
The study of polygons with the tools we have right now might be a little boring, so we first need to
introduce measures (after all, this is not chapter 2). Distances on the sphere are measured on the surface of
the sphere and using geodesics (great circles). This distance can be shown to be proportional to the standard
distance (in the three-dimensional Euclidean space). Angles will be measured by either the 3 − D direction
that a great circle points at when starting from the vertex, or equivalently, by consider the angle between
the planes that determine the great circles.... wait, what angle between planes?
Definition 11 The dihedral angle between two planes (or angle between two planes) is obtained by measuring
the angle created by the planes’ normal vectors.
P
N!
"
NP
!
Figure 3.3: Dihedral angle between planes P and Π
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
38
Figure 3.4: Spherical triangle
We will start studying triangles, because they are the simplest objects to look at, and because they are
always simple polygons. A spherical triangle is obtained by three non-concurrent great circles.
Euclidean triangles separate the plane into two disjoint pieces, that can be called the interior and exterior
of the triangle. This situation also holds on a sphere but now it is not so clear what is the inside and what
is the outside of the triangle. Thus three non-concurrent lines will define two triangles.
Figure 3.5: Two spherical triangles with same three sides
Note that only one of these triangles could be contained in a hemisphere. This triangle will be the one
we mean when we talk about the triangle formed by any three given vertices.
One of the facts that is very easy to notice does not work in spherical triangles is that the sum of their
interior angles will not always add up to 180o . For instance, the large triangle in figure 3.5. But we can even
find examples of this in ‘small’ triangles. In fact any triangle formed by two vertices on the equator and the
North pole will be isosceles with right base angles. The obvious question now is if this is the case for all
spherical triangles. In order to answer this questions we need to take a look at a special kind of polygon we
don’t find in Euclidean geometry: lunes.
Definition 12 A lune is a 2-gon on a sphere.
Figure 3.6: A lune with vertices the North and South pole.
We will use lunes as ways to measure area, and we will discover that the area of a triangle is closely
related to the sum of its interior angles.
Remark 4 The two interior angles of a lune are congruent. Also, the area of a lune is
A = 2αr2
where α is the angle (in radians) that determines a lune, and r is the radius of the sphere.
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
39
Theorem 7 (Girard) Let 4 be a spherical triangle with interior angles α, β and γ, then its area is
A4 = r2 (α + β + γ − π)
where r is the radius of the sphere.
Proof. 4 can be considered as the intersection of three lunes, each having sides a pair of sides of the triangle
and having angles α, β and γ. This can be clearly seen in figure 3.5. Let us call these lunes Lα , Lβ and Lγ .
Now notice that there are three more lunes created from drawing the complete great circles that are the
sides of Lα , Lβ and Lγ . It is clear that these three new lunes have angles α, β and γ, and thus have the
same area as the original three lunes (Why?). Also, these lunes will intersect in a triangle that is congruent
to 4 (Why?).
Since these six lunes cover the sphere completely and overlap only to form two copies of 4, then the sum
of their areas is the area of the sphere plus four times the area of 4. Hence,
4πr2 + 4A4 = 2 2αr2 + 2βr2 + 2γr2
which implies the formula we wanted (Why?).
Corollary 3 The sum of the interior angles of a spherical triangle is always more than 180o . Moreover, the
larger the triangle the more over 180o the sum of its interior angles is.
Definition 13 The excess of a spherical triangle is how much over 180o (or π) the sum of its interior angles
is.
Remark 5 Recall that similar triangles must have the same corresponding angles. It follows that in spherical
geometry this will force the triangles to have the same area (and same angles), thus making the triangles
congruent.
Let us move on to circles. We define a circle in the usual way, as the set of points that are at the same
distance from another fixed point. The difference now is that distances are measured on the sphere by using
great circles.
The first important fact to note is that a circle on a sphere is formed by cutting the sphere by a plane.
In fact, if the center of the circle is the North pole, then this plane is parallel to the plane that defines the
equator. Also, the points on a circle are not only at the same distance from the center on the sphere but
also in the Euclidean 3 − D space.
Cylinders and cones
Let us first look at the cylinder, and infinite cylinder that is. As mentioned before, this is a smooth surface,
and thus the local geodesics will determine what we will call lines on a cylinder. So, let us think as if we
lived on a cylinder.
By using the same type of tricks we used on the sphere, it is easy to see what is a straight line that joins
two points that are one on top of the other, or are on one of the circles that form the cylinder.
Figure 3.7: Cylinder with a ‘vertical’ line and a ‘horizontal’ line.
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
40
Figure 3.8: Cylinder with a helix as a line.
The question is more interesting when we want to join two points that are not in either of the two
positions described above. Probably the easiest way to do this is to try to join to points that are fairly closed
(recall the local property of geodesics) with a string. Once the local stuff is clear, we just need to extend
these lines in the same direction... whatever that means. We obtain helixes as lines, awesome!
There are several things that go wrong with these lines. For example, horizontal and vertical lines
intersect in one point but a vertical line and a helix line will intersect in infinitely many points! But this is
even worse, because at least vertical and helix lines are lines of different type. In fact there are at least two
helix lines connecting two points that cannot be joined by horizontal or vertical lines. Also, some lines have
infinite length and other have finite length. So, a cylinder with its lines is not even close to be a standard
Euclidean plane.
However, if we draw a vertical line `, and we set it as a limit for the length of lines, i.e. once a line
touches ` the line stops. By doing this we get the same horizontal and vertical lines, and a unique helix
line going through any two points not on horizontal/vertical lines. Moreover, now vertical and helix lines
intersect in exactly one point.... the only problem is that an ‘old’ helix line now is infinitely many ‘new’
helix lines. Odd. Anyway, with this new ‘rule’ we have that any two points do determine a unique line, but
I guess the restriction is too much to ask.
For an infinite cone we cannot use the fact we used before about geodesics on smooth surfaces, as the
vertex is sharp point (non-smootheness follows from here). However, we can use the tools we used on the
sphere to explore what straight lines should be on a cone. However, we first have to realize that there are
many different types of cones, and that what makes them different is essential and not just like the radius
of a sphere or radius of the circle used to construct a cylinder. Well, let us start with a definition.
Definition 14 A cone is the surface obtained by rays with initial point the center of a sphere and passing
through all the points on a simple curve drawn on the sphere.
Figure 3.9: A real cone.
Of course, this is not what we are used to think about when a cone is mentioned. We would prefer
something with a circular base, some sort of infinite ice cream cone. Note that if the curve drawn on the
sphere that determines the cone is a spherical circle then we get one of these cones. From now on these will
be the only cones we will consider.
If we make a cut from the vertex of the cone following one of the rays that creates the cone we will be
able to unfold the cone and create something like.
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
41
!
Figure 3.10: Open cone.
The picture above may change from cone to cone, as the angle α can take any non-zero value. We will
call α the cone angle. This angle determines how steep the cone is, the smaller the angle the steeper the
cone is. You should experiment at this point with different angle cones to see why this is true. While you
are at it you should also take a string and experiment on what straight lines on a cone should be. Do you
see any difference between cones with different angle cones?
If two points are on one of the rays that define the cone, then it is easy to see that the line joining then
is given by the ray that contains them. Note that this takes care of all lines through the vertex of the cone.
The situation is more complicated for points that are not collinear with the vertex. In this case the string
experiment (previous paragraph) yields a very nice surprise; some kind of helix line spiraling towards the
vertex of the cone. What is interesting about these lines is that their behavior depends on the cone angle.
In fact, if the cone angle is more than 180o then nothing too special occurs, but if it is less than 180o then
these lines intersect themselves! Even worse, if the cone angle is less than 90o then these lines intersect at
least twice... not good.
Covers
Arguably the most important ideas used in the combinatorial study of manifolds are identification of points
and covers. The plan is to study a space S by looking at a (hopefully) simpler space that can be ‘wrapped’
around S.
As a first example construct a cone by rolling a piece of paper and taping two opposites edges of the
paper. If we now consider a piece of paper that is twice as wide as the first one then we can wrap this piece
around the cylinder twice. It follows that an infinite-width piece of paper will wrap around our cylinder
infinitely many times. From here it is not so hard to see that the Euclidean plane can be wrapped around
an infinite cylinder infinitely many times.
Now let us come back to the cylinder you constructed, which have been wrapped around by another
larger piece of paper, let us say, 5 times. Next take a pin and pierce the cylinder (still wrapped) in any
point you want. Be careful of going through all the layers of paper without piercing any other point of the
cylinder. When you unwrap the larger piece of paper you will see exactly 5 holes, all these points correspond
to that unique hole in the cylinder.
If we call P to the point/hole in the cylinder, then the other five points that correspond to P in the larger
piece of paper are called the fiber of P , and the large piece of paper is called a 5-fold cover (or covering) of
the cylinder. What is interesting is that the points on the fiber of P , with their immediate surroundings,
look just like P and its surroundings. Well, since geodesics turned out being a local thing, why don’t we take
a look at the geodesics of the points in the fiber of P to see what the geodesics around P could be? Will
we get the same ‘straight’ lines we found by observation in the previous section? Experiment and realize
this occurs. In fact we can construct n-fold covers of the cylinder for all positive integer n and this situation
repeats.
Sometimes covers are not as good as the ones we found for the cylinder, where all lines through any
point can be found looking at the same cover. On the sphere we can think of a (pretty much) cover by the
whole Euclidean plane. In order to do this we consider a sphere with radius one and center the origin of the
standard three-dimensional space. Thus, the southern hemisphere is below the x − y-plane and the other
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
42
half is above. Of course, the equator is on that plane.
For any point P on the sphere we draw the line joining the North pole with P , this line must intersect
the x − y-plane at some point P 0 , this point is called the projection of P from the North pole.
N
P
P’
Figure 3.11: P 0 is the projection of P from N .
Note that points on the southern hemisphere project to the circle delimited by the equator and the points
on the northern hemisphere will project to points outside this circle. It is possible to show that every point
on the x − y-plane is the projection of some point on the sphere. This projection of all the points on the
sphere (not the North pole) onto the x − y-plane is called the stereographic projection.
A way to think about this map is what we do when one wants to wrap a baseball in a sheet of paper
that is just big enough to cover the ball. Of course, the big difference is that in the case of the stereographic
projection the sheet of paper is infinitely large and thus it needs to ‘shrink’ in order to cover the finite surface
of the sphere. We can see now that the plane could be considered as a 1-fold cover of the sphere (helped
with the stereographic function). However, we cannot forget that the North pole will stay uncovered.
Now, just as we did with the cylinder, we consider the set of lines on the x − y-plane that pass through
the origin. It is easy to see that after the stereographic covering is applied to them we get (sphere) lines
through the North pole. Then again, a (pseudo) cover is giving us the lines in the space we want to study
for free.
When we talked about cylinders and cones we did not discuss certain topics that we did talked about on
the sphere. For instance, angles and circles. Hence, the obvious question would be if the stereographic projection would also give us angles and circles on the sphere for free. Well, it does! This is a project/presentation
topic.
For the cone most things depend on the cone angle, we have already seen this strange behavior when we
realized that the the number of times a line will self intersect depends on the cone angle. A trivial cover of
the cone is given by the way we would construct a cone if we were given a sheet of paper. We would tape
together two consecutive edges of the sheet... we have just found a 1-fold covering of that cone!
Following the idea used to find a 1-fold covering of a cone by a sheet of paper we can construct a 2-fold
covering by just going twice around the cone before taping the edge to the previous layer of paper (note this
covering is not double at the vertex of the cone). This process can be easily generalized to construct n-fold
coverings of a cone (minus the vertex!). The only problem with this generalization is that we will need to
tape lots of sheets side by side to be able to wrap the cone over and over again.
Let us focus on a cone with cone angle measuring 45o . With a sheet of paper construct a 4-fold covering
of it. Now draw the three lines that are identified with the edges of the sheet after covering the cone, these
lines should be concurrent at the (one) point that will cover the vertex of the cone. So far we have partitioned
the sheet into 4 pieces that do not quite look the same. The idea is that we should do this with an infinite
sheet of paper covering an infinite cone, in this situation we will have 4 congruent parts completing the cover
space.
Then, similar to what we did with the cylinder, pierce the surface of the cone (and cover) without crossing
the opposite side of the cone. In this way we will get 4 points on the sheet that will be identified with each
other after doing the covering. You should get something like.
Now draw a straight line on the sheet and then wrap it around the cone to see what the line becomes,
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
43
Figure 3.12: A 4-fold covering of a 45o cone.
you will see it will give you one of the weird lines we had found before! Note the self intersections. One
way to see these self intersections on the cover is to copy/identify the pieces of the line that are on distinct
quarters of the cover and paste them into one quarter. Also note that if you draw any straight line on the
cover that contains the point that will cover the vertex of the cone you get one of the straight lines on the
cone we also had suspected existed.
We will now use the idea of cover to study what lines should be on a torus. We haven’t looked at this
space by itself, but by now we feel comfortable enough with the idea of a space inheriting the geometry of
its cover to play with ‘the donut’.
We consider a square and we tape its two pairs of parallel sides, this taping creates an identification
of the points on the sides of the square, this identification can be seen in the following picture (where two
points of the same color are considered to be the same after taping/identifying.
Figure 3.13: A square with identified sides that yields a torus.
Note that a torus is nothing but a cylinder with top and bottom identified. Also note that the four
vertices of the square are identified to one point on the torus.
The previous square yields a 1-fold covering of the torus (except for the two curves where a pair of
opposite sides meet, and the point where these curves intersect). For an n-fold covering we need to consider
many of these squares at the same time. For example, the following picture is a 6-fold covering of a torus.
Figure 3.14: A 6-fold cover of a torus.
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
44
Probably the most interesting cover of the torus is the whole Euclidean plane. This is an ∞-fold covering!
We create the squares by drawing all lines y = a and x = b for all a, b ∈ Z and we identified their sides just
like picture 3.13.
Now we take two points that are the same under the identification and draw a line through them (this is
to assure that the line will be closed, that it will not go forever). We get something like
We identify all the pieces of the line that are in different squares and we put them in one. We get
When this square is bent and folded to create a torus we will get a curve that will be a line in the torus.
If you think this curve as a piece of thread that will wrap around the torus then it will go around the torus
4 times in one direction and once in the other direction. Just like in the next figure the coil goes around the
torus 12 times in one direction and once on the other.
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
45
Exercises
1. Give a convincing argument that given two points on a sphere, the shortest path between them will
be given by a great circle.
2. Show that every small circle is parallel (in 3 − D space) to some great circle.
3. Find the ratio of the distance in 3 − D space and the distance on the sphere between two points on
the sphere.
4. Show that there are no geodesics on the sphere besides great circles.
5. A bear walks for 1 mile due South, then 1 mile due East, then 1 mile due North, returning to the exact
place where it started. What color is the bear?
6. Show that two distinct great circles always intersect in exactly two (antipodal) points.
7. Show that two great circles on a hemisphere intersect exactly in one point.
8. Prove remark 4.
9. Finish the proof of Girard’s theorem and prove corollary 3.
10. Find the formula for the result of Girard’s theorem when the angles are measured in degrees instead
of radians.
11. Extend Girard’s theorem to (simple, convex) polygons.
12. Look at Girard’s formula and think about a small triangle drawn on Earth’s surface... since the radius
of Earth is so big, what can we say about the excess of that triangle?
13. How big can the sum of the interior angles of a spherical triangle be? Is this value actually reached?
Is it possible to obtain all possible angle-sums up to that value?
14. Does the Pythagorean theorem hold on spheres?
15. Do SSS, ASA, and SAS hold on spheres? Does that theorem saying that the measure of an exterior
angle of a triangle is equal to the sum of the opposite two interior angles work on spheres?
16. Show that a circle on a sphere is formed by cutting the sphere by a plane. Describe this plane. Is the
converse true?
17. Show that the points on a circle are equidistant from the center of the circle in the Euclidean 3 − D
space. Find this distance in terms of the radius of the circle and the radius of the sphere.
18. Get the area and perimeter of a circle on a sphere in terms of its (spherical) radius.
19. We know that π can be obtained from any circle by dividing the circle’s perimeter by its diameter. Is
this possible on a sphere? In case it is possible, what value do we get for π ? Is this consistent with
the perimeter of a circle with radius 1 being 2π?
20. is there a largest triangle on the sphere? Is there a largest circle? Is it possible for a circle to become
so large that is is a line? What about these questions on the Euclidean plane?
21. Show that for any two points on a cylinder that cannot be joined by a vertical or horizontal line there
are infinitely many helix lines that join them.
22. Show that ‘new’ lines on the cylinder actually do well-behave as described in the text.
23. What is a cone with cone angle equal to 360o ?
CHAPTER 3. CYLINDERS, CONES, SPHERES, ETC.
46
24. Show that the set of lines on the x − y-plane that pass through the origin are mapped, under the
stereographic projection, to (sphere) lines through the North pole.
25. Using the idea discussed before and after figure 3.12 get a formula for the number of self intersections
of a (weird) line on a cone. This formula should depend on the cone angle.
Hint: You should try coverings for many different cones (meaning different cone angles) to figure what
is really causing the self intersections. Also, don’t forget that you are modeling a cover of an infinite
cone.
26. (Hard) Show that there is a line on the torus that passes through every point of the torus exactly once.
Chapter 4
Basic neutral geometry
Arguably the most important math book in history is Euclid’s Elements. A 13 volume treaty, written about
2300 years ago, that compiled all the mathematical knowledge of that time in a increasing manner, meaning
that at the beginning one can find the very basic and essential and then later it all gets more complex and
fancier. So, the first book contains definitions and a few ‘obvious’ or ‘evident’ facts that needed no proof
and that will be crucial to develop future results.
These evident facts were called common notions and postulates. The earlier are general ideas, not
necessarily geometric. The latter are purely geometric and contain a very controversial ‘evident’ fact... the
fifth. Most of the theorems that are taught in schools today are in the Elements. Euclidean has shown to
be great to solve ‘real life’ problems, as is what engineers use to design buildings, bridges, etc.
The study of shapes and their properties (sometimes called geometry) that avoids as much as possible
the use of the fifth is called neutral geometry. In order to learn about this geometry we need to review the
work of Euclid first.
Euclid’s Elements
What follows has been taken out of Book I of Euclid’s Elements.
Visit
http : //aleph0.clarku.edu/ ∼ djoyce/java/elements/elements.html
for a more complete review of this material.
Definitions
1. A point is that which has no part. We would say now ‘it has no dimensions’
2. A line is breadthless length. We would say now ‘it is one-dimensional’
3. The ends of a line are points. Thinking mostly about segments, what are the ends of a line?
4. A straight line is a line which lies evenly with the points on itself. Kind of using the idea of a line
being self-symmetric
5. A surface is that which has length and breadth only. We would say now ‘it has two dimensions’
6. The edges of a surface are lines. Similar thing as the ends of lines
7. A plane surface is a surface which lies evenly with the straight lines on itself. A plane must contain
all the lines through any of its points
47
CHAPTER 4. BASIC NEUTRAL GEOMETRY
48
8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do
not lie in a straight line.
9. And when the lines containing the angle are straight, the angle is called rectilinear.
10. When a straight line standing on a straight line makes the adjacent angles equal to one another, each
of the equal angles is right, and the straight line standing on the other is called a perpendicular to that
on which it stands.
11. An obtuse angle is an angle greater than a right angle.
12. An acute angle is an angle less than a right angle.
13. A boundary is that which is an extremity of anything.
14. A figure is that which is contained by any boundary or boundaries.
15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one
point among those lying within the figure equal one another.
16. And the point is called the center of the circle.
17. A diameter of the circle is any straight line drawn through the center and terminated in both directions
by the circumference of the circle, and such a straight line also bisects the circle.
18. A semicircle is the figure contained by the diameter and the circumference cut off by it. And the center
of the semicircle is the same as that of the circle.
19. Rectilinear figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than
four straight lines. Polygons!
20. Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle
that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
21. Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled
triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles
acute.
22. Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that
which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and
a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral
nor right-angled. And let quadrilaterals other than these be called trapezia.
23. Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely
in both directions, do not meet one another in either direction. ... being in the same plane...
Important!!! When lines do not intersect in the 3 − D space, it is common to say they are
‘skew’
Common Notions
1. Things which equal the same thing also equal one another. Transitivity
2. If equals are added to equals, then the wholes are equal.
3. If equals are subtracted from equals, then the remainders are equal.
4. Things which coincide with one another equal one another.
5. The whole is greater than the part.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
49
Postulates
Let the following be postulated: Important: kind of assumed here is that all elements considered
are on the same plane, also assumed that lines have infinite length
1. To draw a straight line from any point to any point. A unique line!
2. To produce a finite straight line continuously in a straight line.
3. To describe a circle with any center and radius. Note that the center and the radius must be
known
4. That all right angles equal one another.
5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than
two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the
angles less than the two right angles.
About the 5th :
(a) In a picture, the fifth says that if
A
B
C
"
D
!
E
F
then since the sum of the angles α and β is less than 180o , then the lines AC and BF , once extended
forever, should intersect ‘on the side’ of the line BE where α and β are.
(b) What does ‘on that side’ mean? We are assuming some kind of order or orientation, we never had this
in chapter 2.
(c) Euclid does not use this postulate until proposition 29, thus the first 28 are valid in neutral geometry.
The first 28 propositions
1. To construct an equilateral triangle on a given finite straight line.
Proof. Given segment AB with length r. First draw circles with centers A and B and radius r
(postulate 3). The intersection of these circles is called C (note we have two options for C, choose
either). The triangle 4ABC is equilateral with the given base (we use postulate 1 to construct the
triangle).
CHAPTER 4. BASIC NEUTRAL GEOMETRY
50
C
A
B
2. To place a straight line equal to a given straight line with one end at a given point.
Proof. Given segment AB and a point P . First join P and A with a line (postulate 1). Using
proposition 1 we can find Q such that 4AP Q is equilateral. Now draw a circle centered at A with B
on the boundary (postulate 3).
P
Q
A
B
Extend the segments QA andn QP into lines (postulate 2), call D and E to the intersections of these
lines and the circle already constructed. Now draw a circle centered at Q with D on the boundary
(postulate 3).
∼ AD and that QD ∼
Note that AB =
= QE. Since QA ∼
= QP , it follows that AB ∼
= AD ∼
= P E.
E
P
Q
A
B
D
3. To cut off from the greater of two given unequal straight lines a straight line equal to the less.
Proof. Using the previous proposition we copy the shorter segment and put it at one extreme of the
longer segment. It follows that we can now cut off (literally) the shorter segment from the longer.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
51
4. If two triangles have two sides equal to two sides respectively, and have the angles contained by the
equal straight lines equal, then they also have the base equal to the base, the triangle equals the
triangle, and the remaining angles equal the remaining angles respectively, namely those opposite the
equal sides. Better known as SAS
Proof. Assume that two lengths, a and b, are given and the angle α between them, thus we have a
picture like.
a
!
b
It is pretty clear that there is a unique way to complete that picture to create a triangle. Done.
5. In isosceles triangles the angles at the base equal one another, and, if the equal straight lines are
produced further, then the angles under the base equal one another.
6. If in a triangle two angles equal one another, then the sides opposite the equal angles also equal one
another.
Proof. (Prop. 5 and 6.) We will represent an isosceles triangle as
C
A
B
where AC ∼
= BC.
Extend AC and BC downwards (using the picture above) the same distance (using proposition 2) to
←→
←→
obtain a point F on AC and a point G on BC, thus creating two triangles 4F AC and 4GAB. Since
FA ∼
= GA, ∠ACB is common to both triangles, and AC ∼
= BC then 4F AC ∼
= 4GAB (by SAS). It
∼
follows that ∠F BC = ∠GCB thus forcing the base angles of 4ABC to be congruent.
Moreover, if 4ABC above has congruent base angles (but we don’t know yet it is isosceles), then we
could assume that AC is larger than BC. Using proposition 3 we can find a point D on AC such that
AD ∼
= BC. Now consider 4ABC and 4BAD, note that ∠ABC ∼
= ∠DAB, BC ∼
= AD, and that AB
∼
is common to both triangles, thus 4ABC = 4BAD (by SAS).
It follows that the area of 4ABC equals the area of 4BAD, which is a contradiction. Hence, using a
similar argument for when BC is larger than AC, we get that AC ∼
= BC, and thus the triangle must
be isosceles.
Note that there is another proof for proposition 5 that uses the angle bisector from C, and a proof for
6 that uses ASA. We cannot write those proofs at this points because we haven’t proved ASA and we
haven’t learned how to construct the angle bisector of a given angle.
7. Given two straight lines constructed from the ends of a straight line and meeting in a point, there
cannot be constructed from the ends of the same straight line, and on the same side of it, two other
straight lines meeting in another point and equal to the former two respectively, namely each equal to
that from the same end.
Proof. This confusing proposition says that if 4ABC is given then it is impossible to construct a
second triangle 4ABD, like in the picture below, such that AC ∼
= AD and BC ∼
= BD.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
52
C
C
D
A
A
B
B
If we assume such a triangle can be constructed then we join C and D and consider 4ACD and
4BCD, both isosceles by assumption. It follows that ∠ACD ∼
= ∠ADC and that ∠DCB ∼
= ∠CDB.
Since ∠DCB is ‘contained’ in ∠ACD then ∠DCB < ∠ADC (measures, that is), an similarly ∠CDB >
∠ADC. So, ∠CDB > ∠DCB ∼
= ∠CDB, which is impossible.
8. If two triangles have the two sides equal to two sides respectively, and also have the base equal to the
base, then they also have the angles equal which are contained by the equal straight lines. Better
known as SSS
9. To bisect a given rectilinear angle.
Proof. We first draw a circle centered at the vertex V of α. The intersections of this circle with the
sides of the angle are labeled P and Q. Now we draw two circles with the same radius centered at
P and Q. These circles intersect at R (note we have two choices for R, choose either).
P
R
!
Q
V
Note that the triangles 4V P R and 4V QR are congruent by SSS. It follows that ∠P V R ∼
= ∠QV R.
−−→
Thus V R is the bisector of α.
10. To bisect a given finite straight line.
Proof. The segment AB is given. We draw circles with the same radius centered at A and B. These
circles intersect in two points, which we label C and D. The line through C and D intersects AB at a
←→
point M . We claim that M is the midpoint of AB. Moreover, that the line CD is the perpendicular
bisector of AB.
C
M
A
B
D
The claim follows from the fact that the points C and D are equidistant from A and B and thus
4CBD ∼
= 4CAD. It follows that ∠BCD ∼
= 4ACD, which implies that 4CM B ∼
= 4CM A by SAS.
Hence AM ∼
= M B.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
53
←→
The fact that CD is the perpendicular bisector of AB follows from the fact that the angles ∠AM C is
congruent to ∠CM B and that their sum is 180o .
11. To draw a straight line at right angles to a given straight line from a given point on it.
12. To draw a straight line perpendicular to a given infinite straight line from a given point not on it. The
previous two propositions allow us to draw all types of perpendiculars to a given line
13. If a straight line stands on a straight line, then it makes either two right angles or angles whose sum
equals two right angles.
14. If with any straight line, and at a point on it, two straight lines not lying on the same side make the
sum of the adjacent angles equal to two right angles, then the two straight lines are in a straight line
with one another.
15. If two straight lines cut one another, then they make the vertical angles equal to one another. Corollary.
If two straight lines cut one another, then they will make the angles at the point of section equal to
four right angles. VAT
Proof.
l
m
$
#
!
"
Since α + β = 180o and β + γ = 180o , then α = γ.
Similarly, we get that β = δ.
16. In any triangle, if one of the sides is produced, then the exterior angle is greater than either of the
interior and opposite angles.
Proof. We want to show that in the picture below ∠CBD is larger than both ∠CAB and ∠ACB.
C
A
D
B
Using proposition 10 we find the midpoint of CB, call it E. Then we draw the line from A to E, and
using proposition 2, and postulate 2, we find a point F on it such that AE ∼
= EF . We obtain the
picture
C
F
E
A
D
B
G
CHAPTER 4. BASIC NEUTRAL GEOMETRY
54
where E is the midpoint of both CB and AF . It follows that 4AEC ∼
= 4F EB by SAS, and thus
∠ACB ∼
= ∠F BE < ∠EBD.
We obtain that ∠CAB < ∠EBD in a similar way.
Note that in proof above, we need to find the point F by extending a line until it reaches a desired
length. This is done by assuming that lines extend indefinitely. It follows that for this proposition to
work we need infinite lines.
17. In any triangle the sum of any two angles is less than two right angles.
18. In any triangle the angle opposite the greater side is greater.
19. In any triangle the side opposite the greater angle is greater.
20. In any triangle the sum of any two sides is greater than the remaining one. This is the triangle
inequality
21. If from the ends of one of the sides of a triangle two straight lines are constructed meeting within the
triangle, then the sum of the straight lines so constructed is less than the sum of the remaining two
sides of the triangle, but the constructed straight lines contain a greater angle than the angle contained
by the remaining two sides.
22. To construct a triangle out of three straight lines which equal three given straight lines: thus it is
necessary that the sum of any two of the straight lines should be greater than the remaining one.
Kind of a non-constructability theorem
23. To construct a rectilinear angle equal to a given rectilinear angle on a given straight line and at a point
on it. We can ‘copy’ angles
24. If two triangles have two sides equal to two sides respectively, but have one of the angles contained by
the equal straight lines greater than the other, then they also have the base greater than the base.
25. If two triangles have two sides equal to two sides respectively, but have the base greater than the base,
then they also have the one of the angles contained by the equal straight lines greater than the other.
26. If two triangles have two angles equal to two angles respectively, and one side equal to one side, namely,
either the side adjoining the equal angles, or that opposite one of the equal angles, then the remaining
sides equal the remaining sides and the remaining angle equals the remaining angle. Better known
as ASA
27. If a straight line falling on two straight lines makes the alternate angles equal to one another, then the
straight lines are parallel to one another.
28. If a straight line falling on two straight lines makes the exterior angle equal to the interior and opposite
angle on the same side, or the sum of the interior angles on the same side equal to two right angles,
then the straight lines are parallel to one another.
The previous two propositions say that, in the following picture, if γ = ψ or γ = φ, then
l1 is parellel to l2
m
%
'
"
!
#
$
&
l1
(
l2
Since by now we have covered all what Euclid was able to show without using the fifth we will now
abandon Euclid’s work and we will study the work of more recent mathematicians.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
55
Saccheri-Khayyam and Lambert quadrilaterals
As mentioned before, we will assume only the first four postulates of Euclid, and thus the first 28 propositions
in the Elements. Recall that proposition 16 needs lines to have infinite length so, the neutrality of this
geometry is also relative to the fifth postulate.
Our study will focus on a special class of quadrilaterals, which when considered under this ‘neutral’ view
are called Saccheri quadrilaterals or Khayyam quadrilaterals.
D
C
A
B
Figure 4.1: A Saccheri-Khayyam quadrilateral.
In the picture above we call AB the base, CD the summit, and AD ∼
= BC the arms of the quadrilateral.
Also, ∠ADC and ∠DCB are called summit angles. Note that the two base angles are right.
Theorem 8 The summit angles of a Saccheri quadrilateral are congruent.
∼ 4BAD by SAS, this implies that AC ∼
Proof. 4ABC =
= BD. Then, 4ADC ∼
= 4BCD by SSS. Therefore
∠ADC ∼
= ∠BCD.
Theorem 9 The line joining the midpoints of the base and summit of a Saccheri quadrilateral is perpendicular to both of them. Moreover, the base and summit lie on parallel lines having a common perpendicular.
Proof. Call E and F to the midpoints of AB and CD, respectively. Then, 4DEA ∼
= 4CEB by SAS. It
follows that DE ∼
= CE, ∠ADE ∼
= ∠BCE, and ∠DEA ∼
= ∠CEB. So, 4CEF ∼
= 4DEF by SSS. Hence
∠DF E ∼
= ∠CF E, and thus these angles are right. Also, ∠F EC ∼
= ∠F ED, and so ∠AEF , which is the
union of ∠DEA and ∠F ED, must be congruent to the union of ∠CEB and ∠F EC, which is ∠F EB. In
other words, ∠AEF ∼
= ∠F EB, and that forces them to be right.
←→ ←→
Hence, EF is a common perpendicular to AB and CD, it follows that AB||CD by proposition 27.
Theorem 10 In a Saccheri quadrilateral, the segment joining the midpoints of the lateral sides is perpendicular to the segment joining the midpoints of the base and the and the summit.
Proof. Let E, F , G, and H be the midpoints of AB, CD, AD and BC, respectively.
D
F
G
A
C
H
E
B
Since ABHG is a Saccheri quadrilateral then its summit angles are congruent. Because of the previous
theorem we know that the line that goes through the midpoints of the base and the summit of ABHG is
perpendicular to AB at E. Since the line through E and F is also perpendicular to AB at E then E and F
are collinear with the midpoint of GH. Done.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
56
Theorem 11 The sum of the interior angles of a triangle does not exceed 180o .
Proof. We will proceed by contradiction. Assume that the sum of the interior angles of 4ABC is 180 + ←→
degrees, where is a positive real number. Let D be the midpoint of BC and take E on AD so that
AD ∼
= DE. We get the following picture.
C
E
D
A
B
Using V AT we get that ∠BDA ∼
= ∠EDC, and thus 4BDA ∼
= 4CDE by SAS. This implies that
∼
∼
∠ECD = ∠DBA and ∠CED = ∠DAB, and this implies that the sum of the interior angles of 4AEC is
equal to the sum of the interior angles of 4ABC. Similarly, the sum of the interior angles of 4AEB is equal
to the sum of the interior angles of 4ABC.
Now notice that ∠BAC is formed by ∠CAE and ∠EAB. So, either ∠CAE and ∠EAB is less than
or equal to half of ∠BAC. Thus, we can consider either 4AEC or 4AEB as a triangle having the same
angle-sum as 4ABC but having an angle that is half one of the angles of 4ABC.
WLOG assume that ∠EAB is less or equal than half of ∠BAC. We now repeat the process above with
4ABE and create a new triangle having angle at A half of that of 4ABE and having the same angle-sum.
Then we do it again, and again, and again... eventually we will obtain a triangle 4AP Q with same angle-sum
as 4ABC and angle at A that is less than . This yields a contradiction (with proposition 17), as it would
mean that the sum of the angles not at A of 4AP Q is more than 180o .
Remark 6 The previous proof is similar to the proof of proposition 16, as it uses that lines have infinite
length.
Theorem 12 The summit angles of a Saccheri quadrilateral are not obtuse.
Proof. By contradiction, assume that the summit angles are obtuse. Then the sum of the four angles of the
quadrilateral is more than 360o . It follows that the sum of the interior angles of either 4ABC or 4ACD is
more than 180o , contradicting the previous theorem.
Theorem 13 In a quadrilateral with right base angles (not necessarily Saccheri), if the arms relative to the
base are unequal, so are the summit angles, and conversely, the greater summit angle always lying opposite
the greater arm.
Proof. Consider the picture below, where AD is larger than BC. And E is a point on AD such that
AE ∼
= BC.
D
E
A
C
B
It follows that ABCE is a Saccheri quadrilateral and thus ∠ECB ∼
= ∠CEA. Since a part is less than the
whole then ∠DCB is larger than ∠ECB, and than ∠CEA. Now we use proposition 16 to get that ∠ADC
is less than ∠CEA.
The converse is an exercise.
The following definition is inspired by theorem 11 and the work on triangles we did on the sphere.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
57
Definition 15 The defect of 4ABC is the difference between π (or 180o ) and the sum of the interior angles
of 4ABC.
We know that in Euclidean geometry triangles have defect zero, but we don’t know that is true in neutral
geometry, so there might be triangles with non-zero defect.
Theorem 14 In the following picture, def (4ABC) = def (4ADC) + def (4DBC).
C
$
"
A
&
!
%
#
B
D
Proof. Consider the triangle given above. Note that
def (4ABC)
=
π − (α + β + γ + δ)
=
π − (α + γ + σ) − (β + δ − σ)
=
def (4ADC) − (β + δ − σ)
=
def (4ADC) − (β + δ − (π − τ ))
=
def (4ADC) − (β + δ + τ − π)
=
def (4ADC) + π − (β + δ + τ )
=
def (4ADC) + def (4DBC)
Lemma 1 If there is a Saccheri quadrilateral with acute summit angles, then all Saccheri quadrilaterals
have acute summit angles.
Proof. Let ABCD be a Saccheri quadrilateral with acute summit angles. Let E and F be the midpoints
of its base and summit, respectively. Let A0 B 0 C 0 D0 be another Saccheri quadrilateral with segment joining
the midpoints of its base and summit congruent to EF . It follows that WLOG we can consider E and F to
be the midpoints of its base and summit.
We have two cases, depending if the base of the second Saccheri quadrilateral is smaller or larger than
the base of ABCD. For the first case we get the following figure,
D’
A’
D
A
F
E
C
! "
B
C’
#
B’
If we assume that α is acute then β is obtuse, then γ must be acute to get an angle sum of at most 360◦
for the quadrilateral BB 0 C 0 C.
For the other case we will use the Archimedean property. This case also assumes that α is acute but now
the base of A0 B 0 C 0 D0 is shorter than the base of ABCD. In order to reach a contradiction we will assume
that the summit angles of A0 B 0 C 0 D0 are right. So, in this case, the picture is
CHAPTER 4. BASIC NEUTRAL GEOMETRY
D
D’
58
F
C’
C
!
A
E
A’
0
B
B’
0
Now let us assume we can ‘copy’ EB C F many times and then put all these copies side by side to the
←→
←→
right of EB 0 C 0 F (keeping DC as summit line and AB as base line). The idea is that after many copies the
right angle at C 0 will be copied to the right of the point C creating this picture.
D
D’
F
C’
C
C’’
" !
A
E
A’
B
B’
B’’
Now we look at BB 00 C 00 C and we note that in order for the angle sum of this quadrilateral to be at most
360◦ then β cannot be obtuse. This contradicts the fact that α is acute.
Now we will show that we can ‘copy’ EB 0 C 0 F as we needed it above. We consider only this quadrilateral
←−→
and the lines that contain its summit and base. Then we create a point P on EB 0 such that EB 0 ∼
= B0P ,
←−→0
←−→0
then we construct the perpendicular to EB at P , in this way we obtain a point Q on F C . The picture for
this is
F
C’
Q
E
B’
P
∼ 4P B 0 C 0 because of SAS, as EB 0 ∼
We note that 4EB 0 C 0 =
= B 0 P , the angles at B 0 being right and B 0 C 0
0 0 ∼
is common to both triangles. It follows that ∠EC B = ∠P C 0 B 0 (which implies that ∠F C 0 E ∼
= ∠QC 0 P ),
0
0 ∼
0
0
0
0
0
0
that ∠C EB = ∠C P B (which implies that ∠C EF ∼
= P C . Hence, 4EF C 0 ∼
=
= ∠C P Q), and that EC ∼
0
0 0
0
0
4P QC , which forces EB C F ∼
= B P QC . Done!
Now we need to move on to see that a Saccheri quadrilateral with segment joining the midpoints of its
base and summit not congruent to EF also has acute summit angles.
Consider any length d, construct a Saccheri quadrilateral with segment joining the midpoints of summit
←→
and base having length d as follows: from E find a point G on AB such that the length of EG is d. From
←→
G construct the perpendicular to AB, this will yield point P (the intersection of the perpendicular and
←→
←→
CD). Finally, we extend the perpendicular just constructed below AB to get a point Q on it such that
←
→
GP ∼
= GQ, and from this point we drop a perpendicular to EF creating a new point R (intersection of the
←→
perpendicular and EF ). We get that F RQP is a Saccheri quadrilateral with segment joining midpoints of
base and summit with length d. The picture for all this is,
CHAPTER 4. BASIC NEUTRAL GEOMETRY
D
59
F
C
P
"
A
E
!
G
B
Q
R
We notice that the construction yields ‘half’ a Saccheri quadrilateral, namely EGP F . Because of the
argument used in the first part of this proof we get that α being acute implies that β is acute. Since β is a
summit angle of F RQP then we are done.
The case when the length of EB is larger than d is similar.
Theorem 15 If there exists a triangle with defect 0, then rectangles exist. If a rectangle exists, then every
triangle has defect 0.
Corollary 4 If there is a triangle with positive defect, then all triangles have positive defect.
Now we move onto Lambert quadrilaterals. These quadrilaterals have three right angles, by convenience
we always consider the two base angles to be right.
D
C
A
B
Figure 4.2: A Lambert quadrilateral.
Note that, contrasting with Saccheri quadrilaterals, we are not assuming the arms to be congruent.
Theorem 16 In a Lambert quadrilateral, the fourth angle is not obtuse. Moreover, the side adjacent to the
fourth angle is greater than its opposite side.
Proof. The idea os to construct a Saccheri quadrilateral from the Lambert one given to us. We proceed
←→
by extending the base and summit of the quadrilateral. Then we get a point E on AB so that AB ∼
= BE.
←→
Finally we draw a perpendicular to AB at E creating a new quadrilateral AEF D. See figure below.
D
C
F
A
B
E
CHAPTER 4. BASIC NEUTRAL GEOMETRY
60
Using SAS we can show that 4ABC ∼
= CE, ∠BAC ∼
= ∠BEC (which implies
= 4EBC, which forces AC ∼
∼
∼
∠DAC = ∠F EC), and ∠BCA = ∠BCE (which implies ∠DCA ∼
=
= ∠F CE). It follows that 4DAC ∼
4F EC by ASA. Hence AD ∼
= EF , and thus AEF D is Saccheri.
The results follow from theorems 12 and 13.
Finally, consider the following construction of a Saccheri quadrilateral associated to 4ABC. Let E and
F be the midpoints of BC and AC, respectively. Then we obtain points G and H that are the points where
←→
←→
perpendiculars to EF from A and B cut EF . We get
C
G
H
E
F
A
B
Figure 4.3: The Saccheri quadrilateral associated to 4ABC.
It is easy to show that ABHG is a Saccheri quadrilateral (upside-down, though).
Theorem 17 The sum of the interior angles of 4ABC is equal to the sum of the summit angles in its
associated Saccheri quadrilateral (∠GAB and ∠HBA in our picture).
Equivalent to the fifth
One thing we must be aware of is the facts that many geometric properties we take as granted are not that
obvious as we think. In fact, when studying neutral geometry we can realize that there are impossible to
prove. Many times these results are proved using the fifth, and thus they need to be generalized to be true
when not considering that postulate.
It is possible to show that the fifth is actually equivalent to certain statements (by working in the realm
of neutral geometry). We will discuss a few of these next.
Theorem 18 The following statements are all equivalent
1. If two lines are cut by a transversal so that the angles formed on one side of the transversal add up to
less than 180o then the lines meet on that side of the line (AKA, the fifth)
2. By a point P exterior to a line ` passes exactly one line parallel to ` (AKA Playfair’s axiom).
3. The angle sum of any triangle is equal to two right angles. In other words, each triangle has defect
zero.
4. The summit angles in a Saccheri quadrilateral are right.
5. The Pythagorean theorem.
6. In any triangle, each exterior angle equals the sum of the two remote interior angles.
7. If two parallel lines are cut by a transversal, the alternate interior angles are equal, and the corresponding angles are equal. (AKA proposition 29).
8. There exists some triangle with angle sum is two right angles.
9. There exists an isosceles right triangle with angle sum equal to two right angles.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
61
10. There exists arbitrarily large isosceles right triangles with angle sum equal to two right angles.
11. The angle sum of any pair of triangles is always the same.
12. There exists a pair of similar, but not congruent, triangles.
13. Every triangle can be circumscribed.
14. The fourth angle in a Lambert quadrilateral is right.
15. Rectangles exist.
16. There exists a pair of straight lines that are at constant distance from each other.
17. Two lines that are parallel to the same line are also parallel to each other.
18. Given two parallel lines, any line that intersects one of them also intersects the other.
19. There is no upper limit to the area of a triangle.
20. The area of a triangle is half its base times its height.
21. There exists a circle passing through any three noncollinear points.
22. The circumference of any circle of radius r is 2πr.
23. The area of any circle of radius r is πr2 .
24. For any triangle, there exists a similar noncongruent triangle.
25. Opposite sides of a parallelogram are congruent.
Let us first consider proposition 29, which can be considered as the converse of propositions 27 and 28.
Proposition 29 A straight line falling on parallel straight lines makes the alternate angles equal to one
another, the exterior angle equal to the interior and opposite angle, and the sum of the interior angles on
the same side equal to two right angles.
Now we will show that it is equivalent to the fifth.
Proof. Let us steal the picture from propositions 27 and 28 for this proof.
m
%
'
"
!
#
$
&
l1
(
l2
First assume the fifth, and that in the picture above l1 ||l2 but, for example, β 6= φ.
If β − φ < 0 then γ + = β + (π − φ) = π + (β − φ) < π, thus by the fifth the lines must intersect to the
left of m. Contradiction.
If β − φ > 0 then δ + φ = (π − β) + φ = π − (β − φ) < π, thus by the fifth the lines must intersect to the
right of m. Contradiction.
Hence β = φ.
Now assume proposition 29 and let us prove the fifth. So, in the picture above we assume that δ + φ < π.
If l1 ||l2 then proposition 29 implies that β = φ, and thus δ + φ = δ + β = π. Contradiction.
If the lines intersect to the left of m, then we have a triangle with vertices l1 ∩ l2 and l1 ∩ m and l2 ∩ m.
Two of this triangle’s interior angles are γ = π − δ and = π − φ. Since δ + φ < π then the sum of these
two angles is
(π − δ) + (π − φ) = 2π − (δ + φ) > π
CHAPTER 4. BASIC NEUTRAL GEOMETRY
62
which is a contradiction.
The next proof shows that the fifth is equivalent to Playfair’s axiom.
Proof. Let us assume the fifth. Let l be a line and P a point not on l. We construct the unique line l⊥
that is perpendicular to l through P . Let Q = l⊥ ∩ l. Now we construct the unique perpendicular m to l⊥
through P . It follows that l⊥ is a common perpendicular to m and l, and thus m||l.
Now take any other line m0 through P . We get the next picture
l
m
P
R
m’
l
Q
Following the picture, note that the ∠QP R is less than 90◦ and thus the sum of the angles formed to the
right of l⊥ by this line and l and m0 add up to less than 180◦ . By the fifth l should intersect m0 to the right
of l⊥ .
Note that depending on the picture we might need to ‘relocate’ the point R so we can repeat the argument
above. Since this is always possible, then m is the only parallel to l through P .
Now let us assume Playfair’s axiom. Let us consider two lines l and m and a transversal n such that the
angles to (let us say) the right of n formed by n, and l and m add up to less than 180◦ , also assume that
l||m.
Note that if n is perpendicular to l then Playfair’s axiom and the construction of a parallel used in the
previous part of this proof force n ⊥ m.
If n is not perpendicular to l, then using Playfair’s axiom and the previous construction we get that n is
not perpendicular to m as well. Now drop the perpendiculars to l through P and to m through Q. Because if
the construction used before and the uniqueness of parallels (Playfair’s axiom) then these lines are common
perpendiculars to l and m. We get,
n
B
P
m
l
Q
A
It follows that QAP B is a rectangle! And thus by theorem 13 QA ∼
= BP and QB ∼
= AP . It follows that
∼
4QP B = 4P QA by SSS. But this forces that ∠P QA + ∠QP A = 90◦ , which contradicts our assumption
of having angles to the right of n with sum less than 180◦ (or that n is not perpendicular to l).
Next we show that Playfair’s axiom / fifth postulate is equivalent to the angle sum of a triangle is two
right angles (180◦ , when among friends).
Proof. Let us assume the fifth, and consider a triangle 4ABC
←→
We draw a parallel line to AB through C and then we extend the sides of 4ABC, and then we create a
copy of 4ABC as in the picture below. Note that to create that figure above we are using proposition 29
(proved using the fifth).
←−→
←→
Now, since AB and A0 B 0 are parallel then the angle sum of 4ABC is equal to the sum of the angles at
←
−→
A0 = C that are above A0 B 0 , which is 180o .
CHAPTER 4. BASIC NEUTRAL GEOMETRY
63
C
B
A
C’
B’
A’ = C
B
A
Now we want to show the fifth/Playfair assuming that the angle sum of every triangle is two right angles.
But first we need to show a little lemma assuming the angle-sum of any triangle is 180◦ . Let P be a point
←→
not on l, and θ any given angle, then it is possible to find a point T ∈ l such that the angle formed by P T
and l is less than θ.
The construction starts by dropping a perpendicular to l through P , let Q be the point of intersection
of l and this perpendicular. Now let R ∈ l be such that P Q ∼
= QR. Now let S ∈ be such that P R ∼
= RS.
We get the picture,
P
"
!
"
Q
!
R
S
We note that 90◦ + 2α = 90◦ + α + 2β = 180◦ , and thus 2β = α. We can repeat this argument as many
times as needed, until we get an angle that is less than θ.
Now we are ready to prove Playfair’s axiom. So, let P be a point not on a line l.
We first find a parallel m to l through P by constructing a common perpendicular n to l and m as we
have done before (we call Q = n ∩ l). Now take any other line m0 through P . Since m 6= m0 , then these lines
form an angle α. We will work on the side of n where m0 is ‘below’ m.
n
"
m
P
m’
Q
l
!
T
Using the mini lemma above we find a point T ∈ l such that ∠P T Q = θ < α (see picture above). Note
that, since all triangles have angle-sum exactly 180◦ then ∠QP T = 90◦ − θ > 90◦ − α. It follows that the
CHAPTER 4. BASIC NEUTRAL GEOMETRY
64
segment P T partitions the angle α. What we have found is a line that is ‘above’ m0 and that intersects l. It
follows that m0 intersects l in some point between T and Q. Hence, there is a unique parallel to l through
P.
Let us show that the Pythagorean theorem is equivalent to the fifth. We first notice that the Pythagorean
theorem is proved in standard Euclidean geometry, and thus the only thing to show is that the Pythagorean
theorem implies the fifth. We will do this via the angle sum of a triangle being 180o .
Proof. Let 4ABC be the isosceles right triangle below. We note that there are other smaller right triangles
in the figure
C
a
a
A
h
p
D
B
q
c
Assuming the Pythagorean theorem we get,
2a2 = c2
p2 + h2 = a2
h2 + q 2 = a2
c2 = (p + q)2 = p2 + q 2 + 2pq
By plugging the last three equations into the first one we get
(h2 + q 2 ) + (p2 + h2 ) = p2 + q 2 + 2pq
If one sets
or
q
h
=
p
h
h
q
= = c, then
p
h
h = cp
hc = q
and we plug it into one of the Pythagorean expressions above to get
a2 = (cp)2 + (hc)2 = c2 (p2 + h2 ) = c2 a2
and thus c = 1. It follows that h = p = q. Hence, 4ADC ∼
= 4CDB (by SAS) and both of them are
isosceles. Since the four base angles are congruent and two of them add up to one right angle (looking at
∠ACB), then the base angles of 4ABC also add to one right angle.
Hence, all isosceles right triangles have angle sum equal to two right angles. It follows from theorem 15
that all triangles have defect zero.
CHAPTER 4. BASIC NEUTRAL GEOMETRY
65
Exercises
1. Find a triangle on the sphere that does not satisfy proposition 16. Show how the proof of proposition
16 fails in this triangle.
2. Show the converse of theorem 13.
3. If m and n are distinct lines both perpendicular to the line `, then m and n are parallel.
4. If P is a point not on `, then the perpendicular dropped from P to ` is unique.
5. If ` is any line and P is any point not on `, there exists at least one line m through P which does not
intersect `.
6. Every segment has a unique midpoint, and every angle has a unique bisector.
7. Look at figure 14 and show that def (4ABC) = 0 if and only if def (4ADC) = def (4DBC) = 0.
8. Show theorem 15 using lemma 1.
9. Assume theorem 15 to show corollary 4.
10. If a triangle is subdivided into other triangles, then the sum of the defects of those triangles is equal to
the defect of the original triangle. Now given a triangle with positive defect, construct two triangles,
one with less defect than the given one, and one with more defect than the given one.
11. Show that the quadrilateral associated to a triangle is Saccheri. Also, show that given a triangle its
associated quadrilateral is unique.
←→
Hint: You might want to consider the perpendicular to EF from C, and proposition 26.
12. Show theorem 17.
13. Suppose that 4ABC and 4DEF have the same defect. Suppose the two triangles have a pair of
congruent sides. Show that their associated Saccheri quadrilaterals are congruent.
Chapter 5
Non-Euclidean Geometries
We call non-Euclidean geometry to the geometry obtained when, in neutral geometry, we negate the fifth
postulate of Euclid. In complete rigor, this yields only one type of geometry: hyperbolic geometry. However,
it is customary to ‘relax’ Euclid’s assumption of lines having infinite length, to then obtain a second nonEuclidean geometry: elliptic geometry. The latter is essentially captured by the sphere, as the real projective
plane RP2 is an example of an elliptic geometry.
Maybe the easiest way to describe these three geometries is by using modifications of Playfair’s axiom.
In fact, let P be a point not on a line `, then
I if there are no parallel lines to ` through P , then the geometry obtained is called elliptic,
II if there is exactly one parallel line to ` through P , then the geometry is Euclidean (sometimes called
parabolic),
III if there are more than one parallel lines to ` through P , then the geometry is called hyperbolic).
Hyperbolic Geometry
Just like the sphere is a ‘curved’ space, so is the hyperbolic plane, but the latter curves in the opposite way
of the sphere, it is curved outwards. Thus, it is is not so crazy to take a picture drawn on the sphere, and
then change the curvature of the lines to get a corresponding figure in the hyperbolic plane. For example,
in the figure below we see what a hyperbolic triangle looks, compared to a spherical triangle.
Figure 5.1: Spherical triangle (left) and hyperbolic triangle (right)
Another way to think about the curvature of the hyperbolic plane is to imagine that you have placed your
hand on the surface of a sphere and then, little by little, you flatten your hand until you get it completely
flat. At this point you can place your hand on the Euclidean plane. So far you have transitioned from the
sphere to the standard plane by making your hand less curved. Now imagine you can keep this movement
of your hand in the same direction, now your hand will bend backwards (pretty impossible, I know). Now
your hand could be placed perfectly on the hyperbolic plane.
In order to continue what we were doing in the previous chapter we will define hyperbolic geometry as
what we obtain in neutral geometry after assuming the following axiom.
66
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
67
Axiom 1 (Hyperbolic axiom) The summit angles of a Saccheri quadrilateral are acute.
Our first goal is to show that this axiom implies the modification of Playfair’s axiom mentioned above.
This follows from the fact that the summit angles of any Saccheri quadrilateral are congruent and acute and
thus there are no rectangles in the hyperbolic plane. Since the existence of rectangles is equivalent to the
fifth we have just shown that the hyperbolic axiom negates the fifth. Hence, in the hyperbolic plane the
following hold
1. In a Lambert quadrilateral, the fourth angle is acute.
2. The sum of the interior angles of a triangle is less than two right angles. In other words, the defect of
a triangle is always positive.
3. Playfair’s axiom fails, but since we can always construct a parallel through a point exterior to a line,
then there are more than one parallel through an exterior point to a line.
4. The Pythagorean theorem does not hold.
5. Proposition 29 does not hold.
6. If two triangles are similar, then they are congruent.
7. There is an upper limit to the area of a triangle.
One of the properties that one can partially ‘rescue’ from the ones listed above is proposition 29. In fact,
Theorem 19 Two lines have a common perpendicular (and thus parallel), if there is a transversal which
satisfies proposition 29 (it cuts the lines so as to form congruent alternate interior angles or congruent
corresponding angles).
Moreover, if two lines have a common perpendicular, there are transversals which satisfy proposition 29,
these go through the midpoint of the common perpendicular segment.
Proof. Let l and m be parallel lines with t a transversal satisfying proposition 29. Let P and Q be the
intersection points of t with l and m respectively, and call R to the midpoint of P Q. By drawing any line s
through R that intersects both l and m we get
s
t
P
A
!
l
R
m
!
Q
B
∼ ∠BRQ (by VAT) P R ∼
Using that ∠ARP =
= QR and ∠AP R ∼
= ∠BQR (by hypothesis and VAT) we
get that 4ARP ∼
= 4BRQ, which means that ∠P AR ∼
= ∠QBR.
Considering α to be a right angle yields one direction of the result. On the other hand, by constructing
∠RBQ to be right yields the other direction.
Remark 7 There are parallel lines in the hyperbolic plane that do not have a common perpendicular. We
will see an example of this when we learn about models for the hyperbolic plane.
Also, two lines have at most one common perpendicular, as if they had more than one then a rectangle
would exist.
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
68
Theorem 20 The shortest distance between two parallel lines with a common perpendicular is obtained along
that perpendicular. Also, the distance from any point on one of these lines to the other line gets larger and
larger, the farther the point is from the common perpendicular.
Proof. Let l and m be two parallel lines with a common perpendicular t which meets them at points P and
Q respectively. Let P2 and P3 be any two distinct points on l different from P , construct a perpendicular to
m through P2 , and P3 , and let Q2 and Q3 be the points where the perpendiculars intersect m.
l
P
P2
P3
Q
Q2
Q3
m
We want to show that
P Q < P2 Q2 < P3 Q3 P Q <
Since
P
QP
Q
is
a
Lambert
quadrilateral,
then
∠P
P
Q
is
acute
(less
than
∠P
P
Q
)
and
thus
2
2
2
2
2
2
P2 Q2 . Similarly, P2 Q2 Q3 P3 is a Saccheri quadrilateral, then ∠P2 P3 Q3 is acute, which is less than ∠P3 P2 Q2
(obtuse!!). It follows that P2 Q2 < P3 Q3 .
We know that there are at least two parallel lines through an external point to a line. In fact, there are
infinitely many!
Theorem 21 Let P be a point not on a line l. Then, there are infinitely many lines parallel to l through P .
Each one of these lines has a common perpendicular with l.
Proof. Construct a line m through P that is parallel to l with common perpendicular t (we have done this
before). As in the previous proof, Q is the intersection of t and l.
Now consider a point P2 on m, different from P . We drop a perpendicular
to l from P2 , the intersection
point of this line with l is Q2 . Because of the previous result, P Q < P2 Q2 , so we consider a point R2 on
P2 Q2 such that P Q ∼
= Q2 R2 .
Note that P QR2 Q2 is a Saccheri quadrilateral, and thus its summit and base are parallel, with a common
perpendicular joining the midpoint of the base and the midpoint of the summit of P QR2 Q2 .
Now let us take another point P3 on m, different from both P and P2 . We can repeat the construction
←−−→
←−−→
←−−→
above to obtain a line Q2 R2 that is parallel to l. Let us assume that Q2 R2 and Q1 R1 are the same line. It
follows that P is collinear with R1 and R2 , and that the distance from each of these points to l is the same
(because P Q ∼
= Q2 R2 ∼
= Q3 R3 ). That is a contradiction.
Since every lines has infinitely many points (something we have just realized we need to assume), then
there are infinitely many parallels to l through P .
Recall that triangles have positive defect in the hyperbolic plane. But, we don’t really know if all triangles
have the same defect, or if there are bounds for the defect, etc. Firstly, recall that if a triangle is broken into
two, then the defect of the big triangle is the sum of the defects of the smaller triangles, which means that
the defect cannot be a constant. Now we will use this idea to look at bounds for the defect.
Theorem 22 For any 0 ≤ x ≤ 180◦ there is a triangle with defect less than x.
Proof. Consider 4ABC in the figure below, which is right and has been broken into two right triangles.
Since def (4ABC) = def (4ADC) + def (4BDC). Then, one of these triangles has defect at most
1
def
(4ABC). WLOG assume
2
1
def (4ADC) ≤ def (4ABC)
2
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
69
C
A
D
B
Now repeat the process dropping an altitude from D. We get a new triangle with defect at most half
of the defect of 4ADC. It follows that this new triangle has defect at most a quarter of def (4ABC).
Continuing this process we can obtain a triangle with defect at most
n
1
def (4ABC)
2
which can be as small as one wants (for large n). So, we can find a triangle with defect less than x.
Using models of the hyperbolic plane it is not hard to convince oneself that one can construct triangles
with angle-sum as small as one wants. This would force the defect of a triangle to be as close to π ass one
wants.
Before continuing our way to find a relation between congruence and similarity of triangles, and also
between defect and area, let us look at a congruence criterion for Saccheri quadrilaterals.
Lemma 2 Two Saccheri quadrilaterals are congruent if their bases are congruent and either of the following
facts holds
1. A summit angle of one quadrilateral is congruent to a summit angle of the other quadrilateral.
2. An arm of one quadrilateral is congruent to an arm of the other quadrilateral.
Proof. For both parts we assume the bases are congruent.
1. First of all note that this is not true in Euclidean geometry, rectangles are a counterexample.
If a summit angle of one quadrilateral is congruent to a summit angle of the other quadrilateral, and
one quadrilateral has shorter arms than the other. We get the figure,
F
E
!
!
!
!
D
C
A
B
Now look at the quadrilateral DCEF , its angle-sum is
α + α + (180◦ − α) + (180◦ − α) = 360◦
which is not possible in the hyperbolic plane.
2. If an arm of one quadrilateral is congruent to an arm of the other quadrilateral, and the summit
angles are distinct, then the same four vertices yield two distinct quadrilaterals, in particular yield
two distinct summits, this contradicts the fact that there is a unique line through two points (the two
‘summit points’ of the quadrilaterals would have two distinct lines through them).
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
70
One of the many equivalent statements that are equivalent to the fifth is that there are two triangles
that are similar but that are not congruent. As in hyperbolic geometry we negate the fifth then this cannot
be true! Now we will prove that two triangles having three pairs of corresponding congruent angles must be
congruent. In short, we are going to show a hyperbolic version of AAA.
Theorem 23 Let 4ABC and 4A0 B 0 C 0 be such that ∠ABC ∼
= ∠A0 B 0 C 0 , ∠BCA ∼
= ∠B 0 C 0 A0 , and ∠CAB ∼
=
0 0 0
0
0
0
∠C A B , then 4ABC ∼
= 4A B C .
Proof. If the triangles are not congruent then all pairs of corresponding sides must be incongruent, otherwise
ASA would imply the triangles to be congruent to each other.
WLOG assume that AB is larger than A0 B 0 . Then consider a point D between A and B such that
←→
AD ∼
= A0 B 0 , and let E on AC such that AE ∼
= A0 C 0 (note that E could be between A and C or ‘beyond’
C).
By construction, and SAS, 4ADE ∼
= 4A0 B 0 C 0 , which forces ∠AED ∼
= ∠ACB. This implies that E
must be between A and C, as if it were not then ∠ACB is an exterior angle of a triangle and it is congruent
to an opposite interior angle (∠AED), which is impossible. The following picture shows this situation.
E
!
C
!
A
B
D
Hence, E is between A and C, which gives us the following picture.
C
"
E
"
!
A
!
D
B
But this is yields that BCED has angle-sum equal to 360◦ (which is impossible), unless D = B and
C = E.
Note that the previous theorem says that if AAA holds then the triangles have the same area. Obviously,
if AAA holds then the angle-sum of the triangles is the same. What we will prove next is a stronger result
than the previous one, as we will obtain triangles having the same area by just asking them to have the same
defect.
Theorem 24 If def (4ABC) = def (4A0 B 0 C 0 ) then 4ABC and 4A0 B 0 C 0 have the same area.
Proof. The proof will be in two parts. First we assume WLOG that 4ABC and 4A0 B 0 C 0 have congruent
bases and then we consider the case when the triangles have no pairs of congruent sides.
In the first case we construct the Saccheri quadrilateral associated to 4ABC and 4A0 B 0 C 0 . We know
that the triangles having the same defect implies that the Saccheri quadrilaterals are congruent (take home
exam problem ), in particular the associated quadrilateral will have the same area. We will now show that
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
71
the area of any triangle is equal to the area of its associated Saccheri quadrilateral by cutting and pasting.
Once this is clear the result we want to prove follows immediately..
Consider 4ABC and its associated Saccheri quadrilateral ABHG in the picture below
C
G
H
E
F
A
B
We drop a perpendicular to GH from C, we call P to the point of intersection. It follows (also a previous
assignment) that 4AGE ∼
= 4CP F . This shows what we wanted.
= 4CP E and 4BHF ∼
Now consider 4ABC and 4A0 B 0 C 0 with the same defect but with no pairs of congruent sides. We start
by relabeling if necessary so that A0 B 0 is the longest (or equal) side of 4A0 B 0 C 0 and that AB is the longest
(or equal) side of 4ABC. Moreover, we ask A0 B 0 to be longer than AB.
Consider the Saccheri quadrilateral given above and extend GH to the right of the figure. Using H’s
right angle construct a right triangle with vertices B and H and hypothenuse equal to |A0 B 0 |/2... why can
we construct this triangle?
Note that BH is shorter than BF , which is shorter or equal than |AB|/2. It follows that BH is shorter
than |A0 B 0 |/2.
Call the third vertex of this triangle P . Now we extend B to a line then we find a point Q on this line
such that P is the midpoint of BQ. We get the following picture.
C
Q
G
H
E
A
P
F
B
Note that 4ABQ has one side in common with 4ABC and another side congruent to A0 B 0 (from
4A0 B 0 C 0 ). So, if we prove that 4ABQ has the same defect as 4ABC then we would be done by the first
part of the proof.
In order to show what we need we start by extending GH to the right of the picture and dropping a
perpendicular to this line from Q. If we call the intersection point R then 4QRP ∼
= 4BHP (by SAA),
which forces QR ∼
= HB. We now use this to get 4QRT ∼
= 4AGT (by SAA), where T = GH ∩ AQ. Hence,
AT ∼
= T Q, which forces ABHG to be the Saccheri quadrilateral associated to ABQ.
The converse of the previous theorem is also true, but the proof needs ideas on triangulation of shapes,
which we have not covered in this course. We will skip it.
We want to find a formula that says that the larger the area the larger the defect gets (and vice-versa).
We will just look at an example to see that it makes sense to think that the defect and the area of a triangle
are proportional. Consider an isosceles triangle with defect 2δ, since dropping the altitude will partition this
triangle into two congruent triangles, then the defect of each one of these smaller triangles must be δ, but
also they must have the same area, which is half of the original triangle. It follows that the ratio of the area
of a triangle and its defect stays constant. This result backs the following corollary (sometimes given as a
definition of area).
Corollary 5 Let 4ABC be a triangle on the hyperbolic plane, then
def (4ABC) = Area(4ABC)
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
72
Before moving into studying the two easier models of the hyperbolic plane we will digress a little to study
types of lines and points, and types of parallel lines, so when we look at the models things make a little more
sense.
Definition 16 We will call the result in theorem 21 the ‘hyperbolic parallel axiom’.
Since the proof of theorem 21 implies that the set of lines that are parallel to a line l through a point P
will form different angles with the perpendicular to l dropped from P . It follows that there is an angle that
is the smallest possible among all lines that are parallel to l. It also follows that there will be a smallest
angle to the right and to the left of the perpendicular.
Definition 17 The lines forming the smallest angles with the perpendicular will be still called parallel to l,
all the other lines not intersecting l and passing through P with other larger angles will be called ultraparallel.
From the previous paragraph it follows that there are only two parallel lines to l through P , they are
sometimes called the left-hand parallel and the right-hand parallel. The angles these lines make with the
perpendicular are called angles of parallelism.
Remark 8 Note that if the angle of parallelism is 90◦ then the hyperbolic parallel axiom would be negated.
Hence, the angles of parallelism are acute.
Are these angles of parallelism congruent? Are these two parallel lines special in any way?
Theorem 25 The two angles of parallelism for the same point C ∈
/ l are congruent and acute.
Proof. The fact the angles are acute was discussed in the previous remark. For the other part of the proof
we will use the following picture.
C
A
D
B
F
E
←→
←→
Let the parallel lines be AC and BC. Assume that the angles of parallelism are not congruent, WLOG
∠F CA < ∠F CB.
Let E be a point on l such that ∠F CA ∼
= F E.
= ∠F CE. Now let D be another point on l such that F D ∼
∼
By SAS we get that 4F CD = 4F CE, which implies that ∠F CD ∼
= ∠F CE, that is a contradiction.
Since a parallel line to a given line l is the ‘closest’ line that does not intersect l, then we will say that they
intersect in an ideal point (this pretty much means that they intersect at infinity). Note that any line on the
hyperbolic plane has two distinct ideal points (one to the left and one to the right), these points will most
of the times denoted Ω and Ω0 . Now we might want to consider an ‘extended’ hyperbolic plane by allowing
ourselves to use ideal points. A triangle with one vertex that is an ideal point is called an Ω-triangle (or
omega triangle), these triangles have very similar properties to those of regular/standard triangles. However,
two sides of an omega triangle will have infinite length.
Remark 9 Note that one can modify the argument used above to prove that the angle of parallelism depends
solely on the distance between C and l, which is the length of CF . If this were not true then we would be able
to construct two triangles that would contradict SAS (one of them being an omega triangle and the other
not).
Theorem 26 Let 4ABΩ and 4A0 B 0 Ω0 be two omega triangles. They are congruent if the sides of finite
length are congruent and if a pair of corresponding angles are congruent.
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
73
Proof. By contradiction, assume AB ∼
= A0 B 0 and that ∠ABΩ ∼
= ∠A0 B 0 Ω0 but that the triangles are not
0 0 0
congruent. Then ∠BAΩ ∠B A Ω , because of the four infinite sides have all the same length. But then
one of these angles has to be smaller than the other, which forces (using the previous remark) the triangle
containing the smaller angle to have a third vertex that is not an ideal point. That is a contradiction.
Remark 10 It is possible to show that if two lines are ultraparallel then they have a common perpendicular.
In fact, only ultraparallel lines have a common perpendicular.
A few final remarks.
1. The distance formula for the Poincaré disk D: P, Q ∈ D, and A, B ∈ ∂(D) such that A, B, P and Q
are collinear in the disk.
|P A|/|P B| dD (P, Q) = ln
|QA||QB| 2. There are two distance formulas for the half plane model H+ :
- If P and Q are on a vertical line, and A is the projection of both points on the x-axis then
|P A| dH+ (P, Q) = ln
|QA| - If P and Q are on a semicircular line, and A and B are the endpoints of the semicircle (both on the
x-axis), then
|P A|/|P B| dD (P, Q) = ln
|QA||QB| 3. Both the disk and H+ are conformal models. Thus any study you want to do with angles in the
hyperbolic plane is perfectly fine if done using these models.
4. Circles on the disk and H+ look like regular circles, but the center is not located where one would
expect it, it is shifted away from the boundary of the disk (or the x-axis). That is the only way
distortion affects circles.
Interestingly, a circle centered at the center of the disk is not affected by distortion.
The real projective plane
Consider a sphere of radius one, then identify antipodal points to create a new space RP2 , called the real
projective plane (for instance, the North and South poles of the sphere become the same point in RP2 ).
This space is an example of a non-Euclidean plane with lines having finite length that negates the fifth by
assuming there are no parallel lines (thus the projective label).
The lines, angles, and distances of RP2 are ‘inherited’ from the sphere. For instance, a great circle on
the sphere, after the identification, becomes a line of RP2 . A triangle on the sphere will become a triangle
on RP2 ... but one must be careful, as considering shapes that contain points from opposite hemispheres on
the sphere might become weird once antipodal points are identified.
The main idea is that the real projective plane is ‘half’ of the sphere, and that it inherits all its geometry.
Let us check a few properties of RP2 .
We know that in the sphere two points might be in more than one line, but this happens only when
the points are antipodal. Since antipodal points are identified in RP2 , then there are no points that are
contained in more than one line. So, we have that any two points in RP2 determine a unique line.
Given a line we can extend it forever... well, the length of the line will be finite but you can keep drawing
the line on top of the line you already have, right?
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
74
Clearly there are circles centered at any point, with any radius (if the radius is large, then just go around
and around the sphere/RP2 until you reach the distance required).
All right angles are the same because they are given by planes that have dihedral angle equal to 90◦ .
Thus RP2 satisfies the first four postulates, as mentioned before the fifth does not hold because all lines
intersect (all great circles intersect).
Recall that euclid had assumed without mentioning it that lines have to have infinite length, that is why
when we study neutral geometry we ‘missed’ this space. In RP2 the longest a line can be is half the length of
the equator of the sphere. So, since this radius is one, then the length of half the equator is π. A segment of
length π on the sphere will start at one point and end at its antipodal point. These two points are identified,
so the line in RP2 is ‘one point short’ of length π, but that is not relevant, it is just one point! The maximum
length is reached.
CHAPTER 5. NON-EUCLIDEAN GEOMETRIES
75
Exercises
1. Try to duplicate standard constructions and results in Euclidean geometry but on the models of the
hyperbolic plane. For example, show VAT, the base angles of an isosceles triangle are congruent, etc.
2. Suppose a quadrilateral ABCD has opposite sides congruent. Must the figure be a parallelogram?
Discuss.
3. Show that the summit of a Saccheri quadrilateral is longer than its base.
4. Let Q be the midpoint of the side AC and let R be the midpoint of the side BC of 4ABC.
(a) Show that QR is shorter than half of AB.
(b) Show that QR and AB are ultraparallel.
5. Let A, B, C be three points on a line l and let O ∈
/ l. Let X, Y, Z be the midpoints of OA, OB and OC
respectively . Show that X, Y, Z are not colinear.
Chapter 6
Dissections
In this chapter we will study area by cutting and pasting. In order for this study to hold in the geometries
we have already studied we will need a couple of new concepts.
Parallel transport and holonomy.
Parallel transport is a technique that allows us to create two parallel lines that have congruent alternate
angles (a proposition 29 kind of thing). What we will do is to ‘slide’ one line along the other maintaining
the angle formed between them, when we stop this motion we have obtained a new line that has the same
angle with the line that stayed unmoved.
!
t
!
m
l
Figure 6.1: m is obtained from l by parallel transport along t.
A way to ‘justify’ parallel transport is by drawing a line connecting two points P ∈ l and Q ∈ m by a
line that intersects t at R and such that P R ∼
= QR.
Q
!
t
!
A
R
B
P
m
l
It is easy to see that 4AP R ∼
= 4BQR by AAS. Thus, copying 4AP R ‘along’ t will give us m.
Definition 18 Let P be a simple convex polygon, the holonomy of P, or H(P), is the smallest angle obtained
between a vector v and the vector w obtained after parallel transport v counterclockwise around the sides of
P. The angle must be measured from v to w.
76
CHAPTER 6. DISSECTIONS
77
Remark 11 This definition is valid in either of the three planes we have learned about. If one wanted to
study holonomy on a sphere then one needs to consider polygons completely contained in a hemisphere.
Holonomy is related to the curvature of the plane. The way we will look at it in these notes is a simplification only for the few shapes we will be really looking at, the more general idea of holonomy is studied in
differential geometry.
Consider a triangle on the Euclidean, hyperbolic of projective plane. Let us start with an angle x,
"
%
#
!
x
!"$
%
x
#
$
x
!"#
x
!"#+ x
$
$
2!"%"$ +x
#
!"#"x
%
H(triangle)
The last picture implies (even if H(4) < 0) that
(2π − β − γ + x) + (π − α − x) + H(4) = 2π
and this forces
H(4) = (α + β + γ) − π
It follows that the holonomy of a triangle is zero in the Euclidean plane, it is positive on the projective
plane (and the sphere), and negative in the hyperbolic plane.... I guess that comment on the relation between
holonomy and the curvature of the space makes more sense now.
Recall that we have talked about ‘arbitrarily’ making the curvature κ of the sphere 1 (when the radius
is equal to one as well) and the curvature κ of the hyperbolic plane −1. Under these assumptions we get
Area(4) = H(4)κ
We will use holonomy later when it links to the concept of dissection.
Dissection of polygons.
Suppose that one cuts a polygon P into pieces and then rearrange them to form a new shape S. It is clear
that Area(P) = Area(S). The converse is not that obvious, in fact there is no reason to think it is true.
Definition 19 Two shapes, P and S, are equivalent by dissection (denoted P =d S) if one of the shapes can
be cut into finitely many pieces, which after rearrangement form the second shape.
CHAPTER 6. DISSECTIONS
78
Our goal in this mini-chapter is to show that if two (finite) polygons on either of the three planes that
have the same area must be equivalent by dissection.... because of the lack of time left in the semester I will
mention many results with no proofs.
In the hyperbolic plane and the projective plane (or a hemisphere), the idea is essentially to take a simple
convex polygon and break it into triangles (preserving area and holonomy) and then work with those triangles
separately. Each of these triangles will be equivalent by dissection to its associated Saccheri quadrilateral
(which has the same holonomy as its associated triangle and summit equal to the base of its triangle). Here
is when things get complicated as we want to re-assemble all these quadrilaterals into one unique shape for
each area value. As we will see later, in the Euclidean plane we will use the basic unit of area, a square.
But, on the sphere and hyperbolic plane there are no squares, thus one needs to consider other basic units
of area, such as lunes. We will skip this so we can study what happens in the Euclidean plane.
In the Euclidean plane things work a little easier. Consider a convex simple polygon P and let C be a
point inside P that can be connected to each vertex of the polygon by a segment that is totally contained in
P. This allows us to break the polygon into a bunch of triangles, and of course the are is preserved.
Now any given triangle can be made equivalent by dissection to a rectangle that has the same base as
the triangle, this rectangle is the Saccheri quadrilateral associated to the triangle.
√ Now we want to take the
rectangle (of sides a and b) and convert it into a square of side s (and thus s = ab). We will do this, in a
first case, as follows
E
F
G
s B
C
I
J
A
b
a
H
D
We note that 4EAD ∼ 4JHD, thus
|HJ|
|HJ|
b−s
|HD|
=
=
=
|AE|
s
b
|AD|
which implies
|HJ| =
s2
s(b − s)
=s−
=s−a
b
b
and this forces |F J| = a.
Now we use this to get that 4EF J ∼
= 4ICD by AAS (∠JEF ∼
= ∠DIC, ∠EF J ∼
= ∠ICD, and
∼
∼
∼
F J = CD) and that 4EBI = 4JHD by ASA (∠IBE = ∠DHJ, JH ∼
= HB, and ∠BEI ∼
= ∠HJD).
Hence, we can cut 4JHD and 4ICD out of the original rectangle ABCD and replace them by 4EF J and
4EBI to obtain the square AEF H, which means that ABCD =d AEF H.
Note that the previous construction needs that we are able to construct a length that is the square root
of a given value (I am talking about constructing s), and it uses similarity of triangles, something we haven’t
studied in this course, but it is in chapter 1. Also, the proof above does not cover all the possible cases. The
problem is that we are assuming the segment ED is below the point G. This is not always the case, as we
can see in the pictures below, but this can be fixed by doing some more cutting and pasting in the original
figure to get a new rectangle that does behave like the one we have just studied. In order to do this we need
to assume a property of the real numbers called the Archimedean property
Definition 20 The Archimedean property of real numbers says that if one takes any two (positive) real
numbers x and y, then there is an integer n such that nx > y.
CHAPTER 6. DISSECTIONS
79
This property is used in may areas of mathematics, calculus being one of them (for instance, it is crucial
when one uses − δ to find/prove a limit of a sequence). We will use it to be sure that by copying the same
distance a finite number of times we can create a segment that is longer than any other given one.
Let us consider ABCD and AEF H as we did above, note that ED is above G. Then we break the
rectangle into many congruent pieces so that each one of the pieces is like the case we discussed above (in
the picture below I just cut ABCD into two rectangles),
E
F
E
C
B
G
A
D
H
F
B
C
G
A
D
H
Now by dissecting the smaller rectangles into squares we obtain (by putting all the squares side-by-side)
a ‘taller’ rectangle. We check this new rectangle if the conditions of the previous case hold, if not rinse and
repeat until one gets a good rectangle and then we dissect it into a square.
Thus so far by dissection we have been able to take any polygon with a specific area and obtain a bunch
of squares (note that the area has been preserved). So, what is left is to have a theorem that can combine
a number of squares and put them all together in one bigger square. In fact we just need a theorem that
combines two squares into a bigger square....
c
c
c
a
b
b
a
Figure 6.2: a2 + b2 = c2