* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Quantum Mechanics
Second quantization wikipedia , lookup
Schrödinger equation wikipedia , lookup
Quantum entanglement wikipedia , lookup
Bell's theorem wikipedia , lookup
Renormalization group wikipedia , lookup
Tight binding wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Atomic theory wikipedia , lookup
Quantum teleportation wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Identical particles wikipedia , lookup
Quantum state wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Canonical quantization wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
EPR paradox wikipedia , lookup
Ensemble interpretation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Path integral formulation wikipedia , lookup
Particle in a box wikipedia , lookup
Hidden variable theory wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Double-slit experiment wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Wave–particle duality wikipedia , lookup
Wave function wikipedia , lookup
Probability amplitude wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
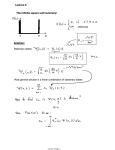
http://www.nearingzero.net Quantum Mechanics introduction to QM “The task is not to see what no one has seen, but to think what nobody has thought about that which everybody sees.” —E. Schrödinger Chapter 5 Quantum Mechanics We get a whole 4 or 5 days to cover material that takes a graduate course a semester to cover! Bohr’s model for the atom seems to be on the right track, but it only works for one-electron atoms… it doesn’t work for helium… it doesn’t account for spectral line intensities… it doesn’t account for splitting of some spectral lines… it doesn’t account for interactions between atoms… and we haven’t explained “stationary states.” Looks like we’ve got some work to do. You may be on the right track, but… you’ll get run over if you just keep sitting there. 5.1 Quantum Mechanics In Newtonian mechanics, if you know the position and momentum of a particle, along with all the forces acting on it, you can predict its behavior at any time in the future. We’ve already seen that because particles have wave properties, you can only measure approximately where a particle is or where it is going. You can only predict where it probably will be in the future. Argh! This could be annoying! Comments: much of chapter 5, especially the first half, is rather dry and mathematical (although the math is not difficult). It is also rather abstract. You may just have to grit your teeth and bear it. Quantum mechanics is a way of expressing the conservation laws of classical mechanics so that they encompass the wave particle duality which we have been studying. Quantum mechanics takes the fundamental laws of classical physics and includes the wave properties of matter. I have already mentioned wave functions before. Let's review wave functions for a minute. Then we will discuss the wave equation. (Kind of backwards, huh?) The symbol we use for the wave function is (“si”, rhymes with “pie”), which includes time dependence, or , which depends only on spatial coordinates. In other words, = (xyzt) and = (xyz). Quantum mechanics is concerned with the wave function , even though itself has no direct physical interpretation. The absolute magnitude evaluated at a particular time and place tells us the probability of finding the system represented by in that (xyzt) state. If the system described by exists, then * dV = 1 . - That is, the system exists in some state at all times. Such a wave function is normalized. The wave function must be well-behaved: and its derivatives continuous and single-valued everywhere, and must be normalizable. See Beiser page 163. Good ideas for quiz questions. could represent a single particle or an entire system. Let’s use the “particle” language for a while. In one dimension, the probability of finding the particle represented by between x1 and x2 is x2 x1 * dx . Let’s do an example. Suppose (x,t) = Ax, where A is a constant. has no time dependence in it; it doesn’t change with time, so we can just write (x) [or (x)]. Is “well-behaved?” and its derivative are single-valued and continuous, but it is not normalizable because the integral of * “blows” up: Here is . Here is *. The red area represents the value of the integral. What do we get if - < x < ? However, if we restrict this particle to a “box,” then is normalizable. So for my example wave function I will use (x) = Ax, for 0 ≤ x ≤ 1, and (x) = 0 elsewhere, where A is a constant to be determined. The first step is always to normalize (unless, of course, is already normalized).* If has some “unknown constant,” such as A, in it, you must normalize! *Failure to normalize is the first common mistake. To normalize, integrate: 1= * dV . Wait!* is zero for x < 0 and x > 1, so the integral becomes 1 1 = Ax Ax dx * 0 1 1 = Ax dx 2 0 1 = A2 3 1 x 3 0 3 3 1 0 2 1= A - 3 3 *Failure to use appropriate limits of integration is the second common mistake. A2 1= 3 A= 3. We have just “normalized” : (x) = 3 x for 0 x 1 . Wait a minute, you told me means there was time in the wave function, and means there is no time in the wave function. Where is time? You’re right. You can do this if you want: (x, t) = 3 x for 0 x 1 and all t . That was a lot of work for a stupid little linear function. What good is this? Good question! Answer: now that we know , in principle we “know” (i.e., can calculate) everything knowable about the particle represented by . That’s quite a powerful statement! OK, so give me an example of something we can calculate! Calculate the probability that the a measurement will find the particle represented by between x = 0 and x = 0.5. P(x1 x x 2 ) = x2 x1 * dx 1/2 1 P(0 x ) = ψ*ψ dx 0 2 1/2 1 P(0 x ) = 0 2 3x 3 x dx 1/2 1 P(0 x ) = 3 x 2 dx 0 2 3 1 x P(0 x ) = 3 2 3 1/2 0 3 1 1 P(0 x ) = - 03 2 2 1 1 *Failure to check that the P(0 x ) = . result makes sense is the 2 8 third common mistake. Does this result make sense?* How can we check? Here’s a plot of the wave function. But remember, we don’t measure the wave function. What we measure is proportional to the magnitude of the wave function squared. Here’s a plot of the probability density (magnitude of wave function squared). You “can’t” talk about the probability that the particle is at x = 0.5 (Heisenberg), but you can talk about the probability that the particle can be found within an incremental dx centered at x = 0.5. The red shaded area represents the probability that the particle can be found in 0 ≤ x ≤ 0.5. The blue shaded area represents the probability that the particle can be found in 0.5 ≤ x ≤ 1.0. I got P(0 ≤ x ≤ 0.5) = 1/8. What would you get if you calculated P(0.5 ≤ x ≤ 1.0)? Does it look like the red shaded area is about 1/8 the total area; i.e., the blue shaded area is about 7 times as big is the red shaded area? Links! http://phys.educ.ksu.edu/vqm/html/probillustrator.html http://phys.educ.ksu.edu/vqm/html/qtunneling.html http://www.phys.ksu.edu/perg/vqmorig/programs/java/qumotion/quantum _motion.html http://www.phys.ksu.edu/perg/vqmorig/programs/java/makewave/