Download Electric Potential and Energy

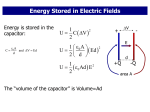
Electric Potential and Energy
The problem:
A conducting sphere of radius R and charge +Q, enclosed by a grounded spherical shell (radius 2R)
and surrounded by a spherical conductor with inner radius of 3R, outer radius of 4R and the total
charge −2Q.
• Find the electric potential and the electric field as a function of r
• Find the work needed to bring a charge q from ∞ to the center of the system
The solution:
The boundary conditions


φ2R = 0,
φ3R = φ4R ,


Q3 + Q4 = −2Q,
are
grounded shell
conductor
given
(1)
The potentials at the shells are
kQ kQ2 kQ3 kQ4
+
+
+
2R
2R
3R
4R
kQ kQ2 kQ3 kQ4
φ3R =
+
+
+
3R
3R
3R
4R
kQ kQ2 kQ3 kQ4
φ4R =
+
+
+
4R
4R
4R
4R
Solving the equations above, we get
(2)
φ2R =
(3)
(4)
1
6
4
Q2R = Q , Q3R = − Q , Q4R = − Q
5
5
5
Substituting the charges into the formulas for the potential of hollow spheres gives
 kQ

, r<R

2R


1
1


kQ( r − 2R ) , R < r < 2R
6
3
φ = kQ( 5r
− 5R
) , 2R < r < 3R


1 kQ

−5 R
, 3R < r < 4R



 4kQ
− 5r
, r > 4R
QR = Q
,
1
(5)
The electric field is the


0
,



kQ


,
 r2 r̂
kQ
6
~
E = 5 r2 r̂
,



0
,



 4 kQ
− 5 r2 r̂ ,
derivative of the potential:
r<R
R < r < 2R
2R < r < 3R
3R < r < 4R
r > 4R
(6)
The work needed to bring a charge +q from ∞ to the center is
U = q∆φ = q(φc − φ∞ ) =
kQq
2R
(7)
2
Electric dipole and capacitors
The problem:
A cylindrical capacitor has length L. The capacitor consists of two conducting cylinderical shells
with a common axis and radii b1 , b2 (b2 > b1 ).
1. What is the capacity of the capacitor?
2. Find the force that acts on the inner cylinder, if it is being pulled along the common axis up
to ∆L above the upper part of the capacitor. (∆L L)
The solution:
1. The capacity is defined as C =
shells using the Gauss’s law
Q
V.
First, we will calculate the field between the cylinderical
Q
l
L
2kQ
E =
Lr
Z b2
2kQ
2kQ b2
∆φ = −
dr = −
ln
Lr
L
b1
b1
L
Q
L
=
C =
= 2π0 b2
b2
V
2k ln b1
ln b1
E2πrl = 4πk
(1)
(2)
(3)
(4)
2. Since ∆L is very small, the change of the capacity will also be very small. The energy of a
Q2
capacitor is given by: U = 12 CV 2 = 2C
. So we presume that the change in the energy will be very
small.
C − ∆C = 2π0
∆U
F
L − ∆L
ln bb21
(5)
Q2 1
Q2 ∆C
1
1 Q2 ∆L
= U (C) − U (C − ∆(C)) =
≈−
−
=
−
2 C
C − ∆C
2 C2
2 LC
2
2
∆U
1Q
Q
b2
= −
=
=
ln
2
∆L
2 LC
4π0 L
b1
The direction of the force is downwards.
1
(6)
(7)
Conductors
The problem:
The inner plate R2 of a cylindrical capacitor is at the potential φ0 , the outer plate R1 is grounded.
Between the plates there is charge distribution with ρ = const. Find φ(r) between the plates.
Answer:
φ=
φ0 + kπρ(R22 − R12 )
r
ln
− kπρ(r2 − R12 )
R1
R
ln R2
1
The solution:
Let the linear density on the inner plate be λ. Gauss theorem gives
Er · 2πrl = 4πk(λ + πρ(r2 − R22 ))l
(1)
so that
Er =
2k(λ − πρR22 )
+ 2πρr
r
(2)
The potential will be
Z r
R1
φ = −
Er (r0 )dr0 = 2k(λ − πρR2 ) ln
− 2πρ(r2 − R12 )
r
R1
Z R2
R1
− 2πρ(R22 − R12 )
φ0 = −
Er (r0 )dr0 = 2k(λ − πρR2 ) ln
R
2
R1
Find λ from the second equation and substitute into the first.
1
(3)
(4)