Download Lecture 10 Induction and Inductance Ch. 30

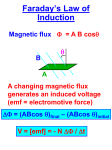
Lecture 10 Induction and Inductance Ch. 30
•
•
•
•
Cartoon - Faraday Induction
Opening Demo - Thrust bar magnet through coil and measure the current
Topics
– Faraday’s Law
– Lenz’s Law
– Motional Emf
– Eddy Currents
– LR Circuits
– Self and mutual induction
Demos


Elmo Problems 15 and 34 Chapter 30
Polling
Demos
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Galvanometer with bar magnet and 3 coils.
2. Gray magnet, solenoid, two LED’s, push and pull, shows different
LED’s light up. Lenz’s Law.
Coil connected to AC source will induce current to light up bulb in second
coil.
Jumping aluminum rings from core of solenoid powered by an AC source.
Cool a ring.
Slowing down of swinging copper pendulum between poles faces of a
magnet. Slitted copper pendulum. Eddy Currents
Inductive spark after turning off electromagnet. Inductance.
Neodymium magnet swinging over copper strip. Eddy currents
Neodymium magnet falling through copper pipe. Then cool with liquid
nitrogen. Eddy currents
Hanging aluminum ring with gray magnet. Lenz’s Law
Two large copper disks with one magnet levitating above another
Introduction
 Stationary charges cause electric fields
(Coulombs Law, Gauss’ Law).
 Moving charges or currents cause
magnetic fields (Biot-Savart Law).
Therefore, electric fields produce magnetic
fields.
 Question: Can changing magnetic fields
cause electric fields?
Faraday's Law
d m
Emf  
dt
• Discovered in 1830s by Michael Faraday and Joseph Henry.
Faraday was a poor boy and worked as a lab assistant and
eventually took over the laboratory from his boss.
• Faraday’s Law says that when magnetic flux changes in time,
an Emf is induced in the environment which is not localized and
also is non-conservative.
• Lets look at various ways we can change the magnetic field with
time and induce an Emf. If a conductor is present, a current can
be induced.
1. What is magnetic flux  m ?
2. What is an induced Emf ?
Demo 1 Thrust a bar magnet through a loop of wire
Magnetic flux

   B  nˆ dA
d
Emf  
dt
Faraday’s Law
Field from Bar
magnet

Units:
A
B is in Tesla
A is in m2
n̂
i
m
is in (Webers) Wb
Current flows in the ring in a
direction that produces a
magnetic field that oppose
the bar magnet.
Lenz’s Law
B produced by bar magnet
B
 0i
2R
at center
Produced by current flowing
in the wire.
Lenz’s Law
The current flows in the wire to produce a magnetic field that
opposes the bar magnet. Note North poles repel each other.
More on Lenz’s Law:
An induced current has a direction such that the magnetic field
due to the current opposes the change in the
magnetic flux that induces the current
Question: What is the direction of the current induced in the ring
given B increasing or decreasing?
B due to induced current
B due to induced current
Demo 2: Gray magnet, solenoid, Red and Green LEDs
magnet
solenoid
B
Green
i
N
N
Red
repel
Push gray magnet in, B field points to the right .
Current starts to flow in coil to produce a field to
oppose the initial field. Red LED lights up.
Pull magnet out, the opposite happens and the Green
LED lights up.
Demo 3: Coil connected to AC source
Light bulb connected to second coil
Coil 2
Iron core (soft)
means lots of inductance in wire so AC
doesn’t heat up wire.
Coil 1
Shows how flux changing through one coil due to alternating current
induces current in second coil to light up bulb. Note no mechanical
motion here.
Demo 4: Jumping aluminum ring from core of
solenoid powered by an AC source.
• When I turn on the current, B is directed upward and
momentarily the top of the iron is the North pole. If the ring
surrounds the iron, then the flux in it increases in the upward
direction. This change in flux increases a current in the ring so
as to cause a downward B field opposing that due to the
solenoid and iron. This means the ring acts like a magnet with a
North pole downward and is repelled from the fixed coil.
induced B
field
induced current
• Try a square-shaped conductor
• Try a ring with a gap in it
• Try a ring cooled down to 78 K
N
Repulsive
force
because 2
North poles
N
Iron core (soft)
Coil
AC source
Motional Emf- field fixed but conductor moves
Pull a conducting bar in a magnetic field. What happens to the free
charges in the material? Moving bar of length L and width W entirely
immersed in a magnetic field B. In this case an Emf is produced but no current
flows


B
W
+

F
Work  qvBL
U  q  emf  qvBL
v

L
-

Fm  qv  B
v
F

Positive charges pile up at the top and negative charges at the bottom
and no current flows, but an Emf is produced. Now let’s complete the circuit.
Motional Emf
What force is required to keep current flowing in the circuit?
Uniform magnetic field into
the screen
Pull the rectangular
loop out of the
magnetic field. A
current i will be
induced to flow in
the loop in the
direction shown. It
produces a
magnetic field that
tries to increase the
flux through the
loop.
Close up
of the wire
Fm  qv  B
F1  iL  B
+
Wire
FA
A= area of magnetic field
enclosed by the wire
v
dm
dA
emf  
 B
dt
dt
Motional Emf Continued
F1  iL  B
F1  BiL
F2  Bix
F3  F2
Lorentz Law
cancel
Faraday and Lenz's Law
d
dA
emf   m  B
dr
dt
d(Lx)
dx
 B
 BL
 BLv
dt
dt
emf  iR Ohms Law
BLv  iR
BLv
i
R
B 2 L2v
F1 
R
Uniform magnetic field into
the screen
R is the resistance
FA
This is the force you
need to pull at to
achieve constant
speed v.
F1=FA
Motional Emf : Work Done by me
How much work am I doing in pulling the circuit?
(Note that the magnetic field does not do any work,)
B 2 L2 vd
W  F1d 
R
What is the rate at which I am doing work? P=Fv
B 2 L2v 2
P  F1v 
R
What is the thermal energy dissipated in the loop?

P  i 2R
BLv
i
R
B 2 L2v 2
P
R
Note that the rate at which I do work in pulling the loop
appears totally as thermal energy.
Circuit diagram for
motional Emf. R is the
resistance of the wire
Eddy Currents
A solid piece of copper is moving out of
a magnetic field. While it is moving out,
an emf is generated forming millions of
current loops as shown.
Eddy currents are also formed in a copper pendulum allowed
to swing across a magnet gap cutting magnetic lines of flux.
Note that when the copper plate is immersed entirely in the
magnet no eddy currents form.
.
• Demo 5: Show a copper plate swinging
through a magnet.
•
For example, in pulling it out, that part of the plate that was in the B
field experiences a decrease in B and hence a change in magnetic flux
in any loop drawn in that part of the copper. An emf is developed
around such loops by Faraday's Law and in such a direction so as to
oppose the change.
induced current
Copper pendulum
Horseshoe
magnet
S
B
N
B induced
Pull back pendulum and
release. Pendulum
dampens quickly. Force
acts to slow down the
pendulum.
• Demo 5 Cont. Also try copper plate with slits. What
happens now?
• Demo 5 Cont. Note inductive spark when turning power
off
• Demo 6: Show neodymium magnet swinging over
copper strip.
Demo 7: Copper pipe and neodymium-ironboron magnet with magnetic dipole moment
Copper pipe
S
N
Two Norths repel so the magnet
drops more slowly.
N
N
B
FD
B
i
d
a
i
N W.M. Saslow Am. J. Phys. 60(8)1977
Cool down the copper pipe with liquid nitrogen
28 K. What do you expect to happen?
FD=Magnetic Drag Force ~
 2 d
a4
 is the conductivity of copper

1

  0 (1   (T  T0 ))  1.69  10 8 (1  0.0043(68  293))
 1.69  10 8 (1  0.96)  0.067  10 8   m
Decreases by a factor of 25 not quite right. Why!!
Demo 8: Hanging aluminum ring with gray magnet
i
N
N
induced B field
B
repel
•
induced current
Note 2 N poles.
Move magnet toward ring – they repel
Current induced in ring so that the B field produced by the current in the
ring opposes original B field.
This means the ring current produces a N pole to push away the N pole of
the permanent magnet.
•
When magnet is pulled back, it attracts the ring.
i
N
N
S
B
Current in ring is opposite
to that above
Changing magnetic field generates electric field
The orange represents a magnetic field pointing into the screen and let say it
is increasing at a steady rate like 100 gauss per sec. Then we put a copper ring
In the field as shown below. What does Faradays Law say will happen?
Current will flow in
the ring. What will
happen If there is
no ring present?
Now consider a
hypothetical path
Without any copper
ring.There will be
an induced Emf with
electric field lines as
shown above.
In fact there
will be many
concentric
circles
everywhere
in space.
The red circuits
have equal areas.
Emf is the same
in 1 and 2, less in 3
and 0 in 4. Note no
current flows.
Therefore, no thermal
energy is dissipated
We can now say that a changing magnetic field produces an
electric field not just an Emf. For example:
Work done in moving a test charge around the loop in one revolution of
induced Emf is
Work  emf  q0
Work done is also
 F  ds  q0  E  ds q0E (2r )
Hence, Emf = 2rE or more generally for any path
Emf   E  ds
But we can not say
 E  ds  
d B
dt
Faraday’s Law rewritten
f
Vf  Vi    E  ds
because it would be 0.
i
Electric potential has no meaning for induced electric fields
Summary
Characteristics of the induced emf
• The induced emf is not localized such as at the terminals of a
battery.
• It is distributed throughout the circuit.
• It can be thought of as an electric field circulating around a
circuit such that the line integral of the electric field taken around
a closed loop is the emf.
• Since the line integral is not 0, the field is non-conservative.
• There are no equipotential surfaces.
• If there is a conductor present, a current will flow in the
conductor.
• If no conductor is present, there is no current flow, only emf.
• Energy is dissipated only if charges are present.
Example: A magnetic field is  to the board (screen) and uniform inside
a radius R. What is the magnitude of the induced field at a
distance r from the center?
x
x
x
x
r
R
x
x
B

dl
x
x
x
x
Field
circulates
around B
field
Notice that there is no wire or
loop of wire. To find E use
Faraday’s Law.
E is parallel
to dl
 Edl  E 2r  
d m
dt
 m  BA  Br 2
d m d
2
2 dB
 ( Br )  r
dt
dt
dt
E 2r  r 2
E
dB
2rE  R 2
dt
r dB
2 dt
dB
dt
rR
R 2 dB
E
2r dt
rR
Example with numbers
Suppose dB/dt = - 1300 Gauss per sec and R= 8.5 cm
Find E at r = 5.2 cm
r dB
E
2 dt
rR
E
(0.052m)
0.13T  0.0034 mV  3.4 mmV
2
Find E at 12.5 cm
R 2 dB
E
2r dt
rR
(0.085m)2
E
0.13T  0.0038 Vm  3.8 mmV
2(0.125m)
What is an inductor?
An inductor is a piece of wire twisted into a coil. It is also called a solenoid.
If the current is constant in time, the inductor behaves like a wire with
resistance. The current has to vary with time to make it behave as an
inductor. When the current varies the magnetic field or flux varies with time
inducing an Emf in the coil in a direction that opposes the original change.
Suppose I move the switch to position a, then current starts to increase through
the coil. An Emf is induced to make current flow in the opposite direction.
Now suppose I move the switch to position b

What is inductance? L
Start with Faraday’s Law
d
Emf  
dt
NAdB

dt
di
  0 nNA
dt
  NBA
B  0 ni for a solenoid
N=nl
di
Emf   0 n lA
dt
l
n̂
2
i
B
N turns
A
di
Emf  L
dt
L  0 n 2 lA
(H=Henry)
1 H=1 T.m2/A
0  4  107 T m/A
L
 0 n 2 A
l
(Henry/m)
Numerical example – how many turns do you need to make a L = 4.25 mh
solenoid with l = 15 cm and radius r = 2.25 cm?
L  0 n 2 lA

n
Ll

0 A
N  nl 
L
0lA
N  nl
(.00425)(. 15)
 565 Turns
4  10 7  (.0225)2
Area
l
n̂
i
B
N turns
A
Show demo: Inductive spark after turning off electromagnet
Numerical Example
You have a 100 turn coil with radius 5 cm with a resistance of 10 . At
what rate must a perpendicular B field change to produce a current of
4 A in the coil?
Emf = IR = (4A)(10) = 40 Volts
dm
dB
2 dB
Emf  N
 NA
 Nr
 40
dt
dt
dt
dB
40
40V


 51T
2
2
s
dt Nr
100  3.15  (.05m)
B(t)
N = 100 turns
N
R = 5 cm
Coil resistance = 10 
N coils so
emf   N
Multiply by N
d m
dt
RL Circuits
VR  Ri

VL

Loop Rule: Sum of potentials =0
  VR  VL  0
di
  iR  L  0
dt
Close the switch to a.
What happens? Write
down the loop rule.
The potential can be defined across
the inductor outside the region where
the magnetic flux is changing.
Solve this equation for the current i.
i

R
(1 e
VR  Ri

Rt
L
)
VR  0.63
VR   (1  e


 

Rt
L
)
R
Ri
L
R
R
L
2000 
4.0H
10 V

VL  e

Rt
L
VL  (e1 )  0.37
Note = L/R = 4/2000 = 0.002 s,
i

R
(1 e1)  0.63

R
and
VR  (1 e1 )  0.63


L
di
dt
How is the magnetic energy stored in a solenoid or
coil in our circuit?
di
  iR  L  0
dt

di
  iR  L
dt
di
2
i  i R  Li
dt
Start with Loop rule or
Kirchhoff's Law I
Solve it for 
Multiply by i

Rate at which energy
is delivered to circuit
from the battery

Rate at which energy
is lost in resistor
Rate at which energy is
stored in the magnetic field
of the coil
dU B
di
 Li
dt
dt
What is the magnetic energy stored in a solenoid or
coil
dU B
di
 Li
dt
dt

dUB  Lidi
2
For an inductor L
UB  12 Li

UB
0
dU B 
i

Lidi
UB 
0

Lidi  12 Li 2
0
Now define the energy per unit volume
U
uB  B
Al

Li 2 L i 2
uB 

Al
l 2A
1
2

Area A
i

l

The energy density formula
is valid in general

Li 2 1
uB 
 2  0 n 2i 2
Al

2
B
uB 
20

1
2
L
 0 n 2 A
l
B  0ni
E2
uE 
20
What is Mutual Inductance? M
When two circuits are near one another and both have currents
changing, they can induce emfs in each other.
1
2
I2
I1
m1  L1I1  M 21I 2
m 2  L2 I 2  M12 I1
M12  M 21  M
On circuit boards you have to be careful you do not put circuits near
each other that have large mutual inductance.
They have to be oriented carefully and even shielded.
Chapter 30 Problem 15
In Figure 30-44, a stiff wire bent into a semicircle of radius a
is rotated at constant frequency f in a uniform magnetic
field B. (Use a, f and B as necessary, with all quantities in
SI units.)
Fig. 30-44
(a) What is the frequency of the emf induced in the loop?
(b) What is its amplitude?
Chapter 30 Problem 34
Figure 30-56 shows two circular regions R1 and R2 with
radii r1 = 12.0 cm and r2 = 34.0 cm. In R1 there is a
uniform magnetic field of magnitude B1 = 50.0 mT into
the page and in R2 there is a uniform magnetic field B2 =
75.0 mT out of the page (ignore fringing). Both fields are
decreasing at the rate of 7.80 mT/s.
•
•
•
•
•
Calculate the integral line int E·ds
for each of the three dashed paths.
(a) path 1
(b) path 2
(c) path 3
Fig. 30-56
Chapter 30 Problem 35
A long solenoid has a diameter of 12.0 cm. When a current i exists
in its windings, a uniform magnetic field B = 27.0 mT is produced
in its interior. By decreasing i, the field is caused to decrease at the
rate of 7.90 mT/s. Calculate the magnitude of the induced electric
field at the following distances from the axis of the solenoid.
(a) 2.20 cm
(b) 8.20 cm