Download PHYS_3342_112911

There will be one last homework assigned today. It will not be due until the
day of the final, Dec 13.
I will also put some practice problems on line today.
There will be a problem solving session tomorrow, Nov 30.
I will not be here next week. The last lecture will be given by another
professor. However, you may email with questions.
The final is Dec 13 at 2 PM. Remember that it will be 40% comprehensive
and 60% on material covered since the last exam. You will be allowed two 8
½ X 11 sheets of paper for notes (both sides) and it is open book.
I will have a review session the day before the final. Look at your schedule
and think about when you would like to have it. I am available all day. We will
discuss this on Thursday.
Motional emf – conductor moving in a constant magnetic field
 B  Blx
FB  qvB will move charges
until compensated by the electric
field of end accumulations
qvB  qE  qV /l
V  Bvl

dx
  Bl
  Blv
dt
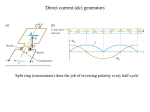
Generators as Energy Converters
I  Blv / R
Presistor  I 2 R  ( Blv )2 / R
Generator does not produce electric energy
out of nowhere – it is supplied by whatever
entity that keeps the rod moving. All it does
is to convert it to a different form, namely to
electric energy (current)
Who does the work?
We! - By moving the bar:
Papplied  Fv  IBlv  ( Blv )2 / R
Energy conserved
After initial push,
Rotating bar :
velocity w ill relax
v(r )  r
Small element :
decelerate d by the
magnetic force :
  Bv dr
d
Total emf :

l
Bl 2
  Br dr 
2
0
2
m
dv
( Bl )
  IBl  
v
dt
R
v  v0 exp( t /  )
  mR /( Bl ) 2
Motion does not
necessarily
mean changing
magnetic flux!
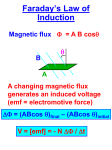
Significance of the minus sign – Lenz’s Law
Induced current has such direction that its
own flux opposes the change of the external
magnetic flux
Magnetic field of the induced current wants
to decrease the total flux
Magnetic field of the induced current wants
to increase the total flux
Correspondingly, magnetic forces oppose the
motion – consistently with conservation of
energy!
Lenz’s Law – the direction of any magnetic induction
effect as to oppose the cause of the effect
Lenz’s Law – a direct consequence of the energy conservation principle
Finding the direction of the induced current
Induced Electric Fields
No matter wha t , the total force on a charge is
F  q (E  v  B )
To have current in the loop, F  0
We did explain currents in moving conductors
(" motional emf" ) with FB  qv  B
BUT! Faraday' s experiment s show that currents
are induced when v  0 but B  B(t )
What is it that drives charges then? Electric field E induced by changing B !

emf
is nothing but the work done to move
a unit charge around the loop once, which is
the line integral around the loop
 E  ds
Electric field around a solenoid with alternating current
Current : I(t)  Imax cos(t)
Magnetic field inside the solenoid :
B(t)  0 nI(t) (outside B  0)
Flux through the surface bounded by the path
B (t)  B(t)  R 2
Electric field circulation around the path
 E  ds  E  2r  
:
:
dB
 0 nImax R 2 sin( t)
dt
Outside : E(r,t) 
0 nImax R 2
sin( t)
2r
 nI r
Inside ( R  r) : E(r,t)  0 max sin( t)
2

B
What Maxwell equation w orks is   E  
t
Using Stokes' theorem :
B
 E  ds  S (  E)  n dA   S t  n dA


 B
    B  n dA   
!!!
t  S
t

The electric field E generated by changing B
is very different from the electrosta tic E :
now it is time - dependent E(t ) and nonconserv ative
Do we need a real circuit to have this field? - NO!
We cannot change magnitude of the velocity of a charged particle
in a static magnetic field B
BUT
We can do it in a time-varying magnetic field B(t) – the resulting
electric field E(t) will do the job
And that’s indeed how particles are accelerated in betatrons!
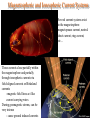
Magnetospheric and Ionospheric Current Systems
Several current systems exist
in the magnetosphere:
magnetopause current, neutral
sheet current, ring current,
etc…
These currents close partially within
the magnetosphere and partially
through ionospheric currents via
field-aligned currents or Birkeland
currents
-magnetic field lines act like
current carrying wires
During geomagnetic storms, can be
very intense
- cause ground induced currents
Geomagnetically Induced Currents (GICs)
Ionospheric currents
• flow at ~100 km
• experience large
spatiotemporal variations
reflected in variations of
the Earth's geomagnetic
field
• as consequence of
Faraday's law of
induction, an electric field
at the surface of the Earth
is induced
• surface electric field
causes electrical currents,
known as geomagnetically
induced currents (GIC), to
flow in any conducting
structure, for example, a
power or pipeline grid
grounded in the Earth
Conducting networks include electrical power
transmission grids, oil and gas pipelines, undersea
communication cables, telephone and telegraph
networks and railways.
Can cause problems, such as increased corrosion of
pipeline steel and damaged high-voltage power
transformers
Historical Events
Known since the mid-1800s:
• electrical telegraph systems could sometimes run without power during
geomagnetic storms, described at the time as operating on the "celestial battery”
• other times completely inoperative.
The Great Storm of 1859
• great Auroras of August 28 and September 4 lit up the skies of nearly every
major city on the planet.
Communication between two telegraph operators:
- Boston operator (to Portland operator): "Please cut off your battery [power
source] entirely for fifteen minutes."
- Portland operator: "Will do so. It is now disconnected."
- Boston: "Mine is disconnected, and we are working with the auroral current.
How do you receive my writing?"
- Portland: "Better than with our batteries on. - Current comes and goes
gradually."
Historical Events
March 24, 1940
• First reported effects on power systems, with voltage dips, large swings in
reactive power, and tripping of transformer banks, reported from power companies
in the US and Canada
• Effects also observed on the telephone and telegraph systems in US
March13, 1989
• severe geomagnetic storm
• aurora seen as far south as Florida and Cuba
• caused the collapse of the Hydro-Québec power grid in a matter of seconds as
equipment protection relays tripped in a cascading sequence of events.
• six million people left without power for nine hours
• eventual cost – $2 billion
Gas pipelines
• currents cause the normal corrosion of pipelines to be accelerated
• modern pipelines protected from long-term current flows by a weak counter
current of a few amperes - applied so that the pipeline has a net, negative potential
relative to ground.
- auroral currents change polarity in minutes, rendering this 'cathodic
protection' useless
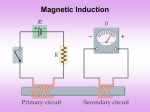
Eddy Currents
When magnetic field is on, currents (eddy currents) are induced in
conductors so that the pendulum slows down or stops
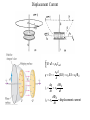
Displacement Current
 B  dl  0 I encl
q  C 
0 A
d
( Ed )   0 EA   0 E
dE
dq
ic 
 0
dt
dt
dE
id   0
 displacement current
dt
Inadequacy of Ampere' s Law for time - varying currents :
 B  ds   I
0
becomes contradict ory
once applied to non - steady currents
Its generaliza tion to one of the Maxwell equations
is a great example of a purely the oretical analysis
of the consistenc y of theory culminatin g in a result
with far - reaching consequenc es
 E
t
Not only currents but changing electric fields too
Maxwell' s generaliza tion :  B  ds   0 I   0 0
give rise to circulatin g magnetic fields! !
c B 
2
j
0
E
 c B  
 0 t
2
j
“displacement
current” of the
electric field
flux as opposed
to conduction
current
0 
1
 0c 2
The Reality of Displacement Current
iD  ic
r2
 B  dl  2 rB  0 R 2 iD
 r
B  0 2 ic  inside the capacitor
2 R
0
B
ic  outside capacitor
2 r
Field in the region outside of the capacitor exists
as if the wire were continuous within the capacitor