Download EM Waves

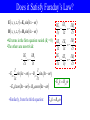
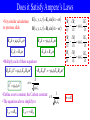
Electromagnetic Waves
Wave Solutions
•Maxwell’s Equations, no sources:
E  0  B
•Changing E-flux creates B-field
  B  0 0  E t 
•Changing B-flux creates E-field
•Can we find a self-sustaining
  E   B t
electromagnetic solution with no sources?
•Let’s try the following:
E  x, y, z , t   E0 sin  kx  t 
B  x, y, z , t   B 0 sin  kx  t 
•I could have used cosine instead, it makes no difference
•I chose arbitrarily to make it move in the x-direction
•We don’t know – yet – anything about k, , E0, or B0.
Does It Satisfy Gauss’s Laws?
E  x, y, z , t   E0 sin  kx  t 
B  x, y, z , t   B 0 sin  kx  t 
E x E y E z


0
x
y
z
•E depends only on x, so there’s only one term in this derivative:

E x

E
sin  kx  t   E0 x k cos  kx  t 
0
0x
x
x
E0 x  0
B x By B z
•This implies E0x = 0


0
•Same argument applies for magnetic fields
x
y
z
B0 x  0
•Note that the electric and magnetic fields are perpendicular to the direction
the wave is traveling
Electromagnetic
waves are transverse
Does it Satisfy Faraday’s Law?
E  x, y, z , t   E0 sin  kx  t 
B  x, y, z , t   B 0 sin  kx  t 
•All terms in the first equation vanish (Bx = 0)
•The others are non-trivial:
By
Ez


x
t


 Ez 0 sin  kx  t    By 0 sin  kx  t 
x
t
Ez 0k cos  kx  t   By 0 cos  kx  t 
•Similarly, from the third equation:
Bx
Ez E y


y
z
t
By
Ex Ez


z
x
t
E y Ex
Bz


x
y
t
 Ez 0 k  By 0
E y 0 k  Bz 0
Does it Satisfy Ampere’s Laws
•Very similar calculations
to previous slide
E  x, y, z , t   E0 sin  kx  t 
B  x, y, z , t   B 0 sin  kx  t 
By 0 k   0 0 Ez 0
Bz 0 k  0 0 E y 0
 Ez 0 k  By 0
E y 0 k  Bz 0
•Multiply each of these equations
By 0 Ez 0k 2  0 0 Ez 0 By 0 2
Bz 0 Ey 0k 2  0 0 Ey 0 Bz 0 2
k 2  0 0 2

k
 0 0
•Define a new constant, the Carlson constant: c 
•The equations above simplify to:
E y 0  cBz 0
Ex
Bz By

  0 0
y
z
t
E y
Bx Bz

  0 0
z
x
t
By Bx
Ez

  0 0
x
y
t
Ez 0  cBy 0
1
 0 0
  ck
Wave Equations Summarized
E  x, y, z , t   E0 sin  kx  t 
•Waves look like:
B  x, y, z , t   B 0 sin  kx  t 
•Related by:   ck
•Two independent solutions to these equations:
B0
or
Ez 0  cE y 0
E0  cB0
E0
E0
B0
E y 0  cBz 0
•Note that E, B, and direction of
travel are all mutually perpendicular
•The two solutions are called
polarizations
•We describe polarization by telling
which way E-field points
•Note E  B is in direction of motion
Understanding Directions for Waves
•The wave can go in any direction you want
•The electric field must be perpendicular to the wave
direction
•The magnetic field is perpendicular to both of them
•Recall: E  B is in direction of motion
E0  cB0
The Meaning of c
  ck
•Waves traveling at constant speed
•Keep track of where they vanish

x  t  ct
kx  t  0
k
•c is the velocity of these waves
c
1
 0 0
E  x, y, z , t   E0 sin  kx  t 
B  x, y, z , t   B 0 sin  kx  t 
 2.99792458 108 m/s
c  3.00 108 m/s
•This is the speed of light
•Light is electromagnetic waves!
•But there are also many other types of EM waves
•The constant c is one of the most important fundamental constants of the universe
Wavelength and Wave Number
•The quantity k is called the wave number
•The wave repeats in time
f 1 T
•It also repeats in space
k  2
  2 f
E  E0 sin  kx  t 
B  B 0 sin  kx  t 
  ck

•EM waves most commonly described
in terms of frequency or wavelength
cf


c
 2 f
k
2
•Some of these equations must be modified when inside a material
The Electromagnetic Spectrum
 Increasing
f Increasing
•Different types of waves are classified
by their frequency (or wavelength) c   f
Radio Waves
Microwaves
Infrared
Visible
Ultraviolet
X-rays
Gamma Rays
•Boundaries are arbitrary and overlap
•Visible is 380-740 nm
Red
Vermillion
Orange
Saffron
Yellow
Chartreuse
Green
Turquoise
Blue
Indigo
Violet
Not these
Know these,
in order
These too
Energy and the Poynting Vector
E0  cB0
•Let’s find the energy density in the wave
u E   0 E   0E sin  kx  t 
2
1
2
1
2
2
0
2
2
B2
B
uB 
 0 sin 2  kx  t 
2 0
2 0
  0c B sin  kx  t  
1
2
u
B02
0
2
1
E0 B0 sin 2  kx  t 
2
1 0 2 2
B0 sin  kx  t 
2  0 0
sin 2  kx  t 
•Now let’s define the Poynting vector:
S
2
0
S
 cu
1
0
E  B
0
•It is energy density times the speed at which the wave is moving
•It points in the direction energy is moving
•It represents the flow of energy in a particular direction
•Units:
J m
W
S uc
3
2
m s
m
Intensity and the Poynting Vector
•The time-averaged Poynting vector is called the Intensity
•Power per unit area
cB02
S c u 
sin 2  kx  t 
0
cB02
S 
2 0
In Richard Williams’ lab, a laser can (briefly) produce
50 GW of power and be focused onto a region 1 m2
in area. How big are the electric and magnetic fields?
P 5.0 1010 W
22
2

5.0

10
W/m
S  
2
6
A
10 m 
7
22
2
2
4


10
T

m/A
5.0

10
W/m
2

S



8
2
0
2

4.2

10
T
B0 

c
3 108 m/s
B0  20,000 T
E0  cB0
E0  6.11012 V/m
Momentum and Pressure
•Light carries energy – can it carry momentum?
U
p
•Yes – but it’s hard to prove
c
•p is the total momentum of a wave and U the total energy
•Suppose we have a wave, moving into a perfect absorber (black body)
•As they are absorbed, they transfer momentum
U
•Intensity:
S 
A
t
•As waves hit the wall they transfer their momentum
cp cF
S 

 cP
At
A
P S c
•Pressure on a perfect absorber:
•When a wave bounces off a mirror, the momentum is reversed
•The change in momentum is doubled
P2 S c
•The pressure is doubled
Cross-Section
•To calculate the power falling on an object, all that matters is
the light that hits it
•Example, a rectangle parallel to the light feels no pressure
•Ask yourself: what area does the light see?
•This is called the cross section
P= S 
F = P
P S c
Sample Problem
A 150 W bulb is burning at 6% efficiency. What is the
force on a mirror square mirror 10 cm on a side 1 m
away from the bulb perpendicular to the light hitting it?
1m
•Light is distributed in all directions
equally over the sphere of radius 1 m
0.06 150 W 
2

0.72
W/m
S 
4 m2
2  0.72 W/m2 
2 S
2
 
 0.1 m 
F  P 
8
3 10 m/s
c
F  4.8 1011 N
Sources of EM Waves
+
•A charge at rest produces no EM waves
•There’s no magnetic field
•A charge moving at uniform velocity produces no EM waves
•Obvious if you were moving with the charge
•An accelerating charge produces electromagnetic waves
•Consider a current that changes suddenly
•Current stops – magnetic field diminishes
•Changing B-field produces E-field
•Changing E-field produces B-field
•You have a wave
–
Simple Antennas
•To produce long wavelength waves, easiest to use an antenna
•AC source plus two metal rods
•Some charge accumulates on each rod
•This creates an electric field
•The charging involves a current
•This creates a magnetic field
•It constantly reverses, creating a wave
•Works best if each rod is ¼ of a wavelength long
•The power in any direction is
S
sin 2 
r2
+
+
+
+
+
+
 –
–
–
–
–
–
Common Sources of EM Waves
Radio Waves
Microwaves
Infrared
Visible
Ultraviolet
X-rays
Gamma Rays
Antennas
Klystron, Magnetron
Hot objects
Outer electrons in atoms
Inner electrons in atoms
Accelerated electrons
Nuclear reactions