Download Document

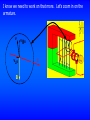
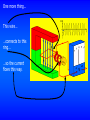
Upcoming Schedule
Nov. 5
boardwork
Nov. 7
21.3-21.5
Quiz 7
Nov. 10
boardwork
Nov. 12
21.5-21.7
Nov. 14
boardwork
Quiz 8
Nov. 17
review
Nov. 19
Exam 3
Chap. 20-21
Nov. 21
18.8
Chapter 22
Nov. 3
20.8, 21.121.2
Must-know facts for all students taking Physics classes:
(1) physicists don't like not knowing things, and
(2) never point this fact out to a physicist.
according to CERN web page (worlds biggest particle accelerator):
physicists don't like not knowing things, and
never point this fact out to a physicist.
Original "homework3.pdf" showed lecture on November 12
covering 21.6. Corrected file shows lecture on November 12
covering 21.5-21.7. I don’t expect to finish 21.5 today, so I
will finish 21.5 on the 12th. I also intended all along to
lecture on transformers (21.7). The homework problem
assignments are unchanged.
21.3 emf Induced in a Moving Conductor
Recall that one of the ways to induce an emf is to change the
area of the loop in the magnetic field. Let’s see how this
works.
v
B
A U-shaped conductor and a

moveable conducting rod are placed

in a magnetic field, as shown.
 ℓ

The rod moves to the right with a

A
speed v for a time t.
vt
The rod moves a distance vt and the area of the loop inside
the magnetic field increases by an amount
A = ℓ v t .
got to here, lect 15 fs2002
The loop is perpendicular to the magnetic field, so the
magnetic flux through the loop is B = BA. The emf induced
in the conductor can be calculated using Ampere’s law:
ΔφB
ε = N
Δt
Δ BA 
ε = 1
Δt
ε =
B ΔA
Δt
B 









v







 ℓ


A
vt
ε =
B v Δt
Δt
ε = B v.
B and v are vector magnitudes, so
they are always +. Wire length is
always +. You use Lenz’s law to
get the direction of the current.
OSE? (not yet)
ε =B v
This “kind” of emf is called “motional emf” because it took
motion to induce it.
The induced emf causes current to flow in the loop.
Magnetic flux inside the loop
increases (more area).
System “wants” to make the flux
stay the same, so the current gives
rise to a field inside the loop into
the plane of the paper (to
counteract the “extra” flux).
Clockwise current!
B 




I





v





vt


 ℓ


A
The induced emf causes current to flow in the loop. Giancoli
shows an alternate method for getting , by calculating the
work done moving the charges in the wire.
Electrons in the moving rod (only the
rod moves) experience a force F = q
v B. Using the right hand rule,* you
find the the force is “up” the rod, so
electrons move “up.”
“Up” here refers only to the orientation on the page, and
has nothing to do with gravity.
B 




I





v







 ℓ


A
vt
Because the rod is part of a loop, electrons flow
counterclockwise, and the current is clockwise (whew, we got
that part right!).
*Remember, find the force direction, then reverse it if the
charge is an electron!
The work to move an electron from the bottom of the rod to
the top of the rod is W = (force) (distance) = (q v B) (ℓ).
Going way back to the beginning of
the semester, Wif = q Vif .
But Vif is just the change in
potential along the length ℓ of the
loop, which is the induced emf.
Going way back to the beginning of
the semester, W = (q v B) (ℓ) = (q ).
F=qvB
B 




I





v







 ℓ


A
vt
Solving (q v B) (ℓ) = (q ) for  gives  = B ℓ v, as before.
I won’t ask you to reproduce the derivation on an exam, but a
problem could (intentionally or not) ask you to calculate the
work done in moving a charge (or a wire) through a magnetic
field, so be sure to study your text.
“But you haven’t given us the OSE yet!”
Good point! The derivation assumed B, ℓ, and v are all
mutually perpendicular, so we really derived this:
OSE
ε = B v 
where B is the component of the magnetic field
perpendicular to ℓ and v, and v is the component of the
velocity perpendicular to B and ℓ.
Example 21-4 An airplane travels 1000 km/h in a region
where the earth’s field is 5x10-5 T and is nearly vertical. What
is the potential difference induced between the wing tips that
are 70 m apart?
The derivation of  = B ℓ v on slides
15 and 16 assumed the area through
which the magnetic field passes
increased.
My first reaction is that the magnetic
flux through the wing is not changing
because neither the field nor the area
of the wing is changing.

































v


True, but wrong reaction! The calculation I did 3 slides back
showed that the electrons in the moving rod (or airplane wing in
this case) experience a force, which moves the electrons.
The electrons “pile up” on the left hand wing of the plane,
leaving an excess of + charge on the right hand wing.
Our equation for  gives the potential
difference.
ε = B v 
ε = 5×10-5 T   70 m   280 m/s 
ε = 1V

































v


+
No danger to passengers! (But I would want my airplane
designers to be aware of this.)
21.4 Changing Magnetic Flux Produces an Electric Field
From chapter 16, section 6:
E=F/q
OSE:
From chapter 20, section 4:
OSE:
F = q v B sin
For v  B, and in magnitude only,
F=qE=qvB
E = v B.
We conclude that a changing magnetic flux produces an
electric field. This is true not just in conductors, but anywhere in space where there is a changing magnetic field.
Example 21-5 Blood contains charged ions, so blood flow
can be measured by applying a magnetic field and measuring
the induced emf. If a blood vessel is 2 mm in diameter and a
0.08 T magnetic field causes an induced emf of 0.1 mv, what
is the flow velocity of the blood?
OSE:  = B ℓ v
v =  / (B ℓ)
In Figure 21-11 (the figure for this example), B is applied  to
the blood vessel, so B is  to v. The ions flow along the blood
vessel, but the emf is induced across the blood vessel, so ℓ is
the diameter of the blood vessel.
v = (0.1x10-3 V) / (0.08 T 0.2x10-3 m)
v = 0.63 m/s
21.5 Electric Generators
Let’s begin by looking at a simple animation of a generator.
http://www.wvic.com/how-gen-works.htm
Here’s a “freeze-frame.”
Normally, many coils of wire are
wrapped around an armature.
The picture shows only one.
Brushes pressed against a slip ring make continual contact.
The shaft on which the armature is mounted is turned
by some mechanical means.
Let’s look at the current direction in this particular freezeframe.
B is down. Coil
rotates counterclockwise.
Put your fingers
along the
direction of
movement. Stick
out your thumb.
Bend your fingers 90°. Rotate your hand until the fingers
point in the direction of B. Your thumb points in the direction
of conventional current.
I can see it for this part of the loop, but have great difficulty
for this part of the loop.
Alternative right-hand rule for current direction.
B is down. Coil
rotates counterclockwise.
Make an xyz axes
out of your thumb
and first two
fingers.
Thumb along
component of wire
velocity  to B. 1st
finger along B.
2nd finger then points in direction of conventional current.
Hey! The picture got it right!
I know we need to work on that more. Let’s zoom in on the
armature.
v
vB
B
vB
I
Forces on the charges in these parts of the wire are
perpendicular to the length of the wire, so they don’t
contribute to the net current.
For future use, call the length
of wire shown in green “h” and
the other lengths (where the
two red arrows are) “ℓ”.
One more thing…
This wire…
…connects to this
ring…
…so the current
flows this way.
Later in the cycle, the current still flows clockwise in the
loop…
…but now this
wire…
…connects to this
ring…
…so the current
flows this way.
Alternating current! ac!
Again: http://www.wvic.com/how-gen-works.htm
“Dang! That was complicated. Are you going to ask me to
do that on the exam?”
No. Not anything that complicated. But you still need to
understand each step, because each step is test material.
Click here and scroll down to “electrodynamics” to see some
visualizations that might help you!
Understanding how a generator works is “good,” but we need
to quantify our knowledge.
We begin with our OSE  = B ℓ v. (ℓ was defined on slide
17.) In our sample generator on the last 7 slides, we had only
one loop, but two sides of the loop in the magnetic field. If
the generator has N loops, then  = 2 N B ℓ v.
Back to this picture:
v
vB
vB
I
B
This picture is oriented differently than Figure 21-13 in your
text. In your text,  is the angle between the perpendicular to
the magnetic field and the plane of the loop.

v
vB
vB
I
B
The angle  in the text is the same as the angle between vB
and the vector v.
Thus, v = v sin .
B is  to the wire, so ε = 2 N B v sin  θ .
But the coil is rotating, so  =  t, and v =  r =  (h/2).
The diameter of the circle of rotation, h, was defined on slide
17.
 h
ε = 2 N B  ω  sin  ωt 
 2
ε = N B h ω sin  ωt 
OSE:
ε = N B A ω sin  ωt 
where A is the area of the loop, f is the frequency of rotation
of the loop, and  = 2  f.
Example 21-6 The armature of a 60 Hz ac generator rotates
in a 0.15 T magnetic field. If the area of the coil is 2x10-2 m2,
how many loops must the coil contain if the peak output is to
be 0 = 170 V?
ε = N B A ω sin  ωt 
ε0 = N B A ω
N =
N =
ε0
BAω
170 V 
 0.15 T   2×10-2 m2   2π×60 s-1 
N = 150 (turns)
You should read about dc motors and alternators in section
21.5, but I won’t test you over that material.