Download CH27-revision-lecture - University of Southampton

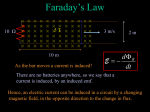
Essential University Physics
Richard Wolfson
27
Electromagnetic Induction
PowerPoint® Lecture prepared by Richard Wolfson
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-1
In Chapter 27 you learnt
• To explain the phenomenon of
electromagnetic induction
• To calculate induced emfs and currents
• To use energy conservation to find the
direction of induced effects
• To describe important technological
applications of induction
• To explain inductance
• And describe the role of inductance in
simple circuits
• That magnetic fields store energy
• And how to calculate that energy
• To recognize Faraday’s law as one of the
four fundamental laws of
electromagnetism
• And to calculate induced electric fields
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-2
Electromagnetic induction
• Electromagnetic induction involves electrical effects
resulting from changing magnetic fields.
• Simple experiments (next slide) show that it doesn’t matter how
the magnetic field changes: Induced electrical effects occur in
all cases of changing magnetic fields.
• (1) Move a magnet near a circuit; an induced current results.
• (2) Move the circuit near a magnet; an induced current results.
• (3) Energize one coil to make it an electromagnet; move it near a circuit
and an induced current results.
• (4) Energize one coil to make it an electromagnet; hold it stationary and
move a circuit near it—an induced current results.
• (5) Change the current in one circuit, and thus the magnetic field it
produces; an induced current results in a nearby circuit.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-3
Five simple experiments
• Experiment 1:
moving magnet
• Experiment 2:
moving circuit/coil
• Experiments 3 and 4:
two circuits; either one moving
• Experiment 5: changing
field/current; no motion
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-4
Faraday’s law
• Faraday’s law, in its simplest form, describes induction
by relating the emf induced in a circuit to the rate of
change of magnetic flux through the circuit:
E 
dB
dt
• Here the magnetic flux is given by
 B   B  dA
• With a flat area and uniform field,
this becomes
 B  BAcos
• The flux can change because of
changing field B, changing area A,
or changing orientation .
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Moving a magnet near a wire
loop increases the flux
through the loop. The result is
an induced emf given by
Faraday’s law. The induced
emf drives an induced current
in the loop.
Slide 27-5
Two examples:
• A changing field
• The loop has radius r,
resistance R, and is in a
magnetic field changing at the
rate dB/dt. The induced emf is
E = πr2dB/dt and the induced
current is I = (πr2/R) dB/dt.
• A changing area
• The bar slides on the conducting
rails, increasing the circuit area at
the rate l dx/dt = lv. The induced
emf is E = Blv, and the induced
current is I = Blv/R.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-6
Clicker question
•
What will be the direction of the current in the loop
when it first enters the field shown, coming into the
field from the left side?
A. clockwise
B. counterclockwise
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-7
Clicker question
•
What will be the direction of the current in the loop
when it first enters the field shown, coming into the
field from the left side?
A. clockwise
B. counterclockwise
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-8
Direction of the induced current: Lenz’s law
• The direction of the induced emf and current is described by the
minus sign in Faraday’s law.
• But it’s easier to get the direction from conservation of energy.
• The direction of the induced current must be such as to oppose that change that
gives rise to it.
• This is known as Lenz’s law.
• Otherwise we could produce energy without doing any work!
• Here the north pole of the magnet approaches the loop. So the induced current
makes the loop a bar magnet with north to the left, opposing the approaching
magnet.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-9
It’s the change that matters
• Lenz’s law says that induced effects oppose the changes
that give rise to them.
• Now the induced current flows the opposite way, making the loop’s
south pole to the left and opposing the withdrawal of the magnet.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-10
Electric generators
• Electric generators use a rotating coil in a magnetic field to convert
mechanical to electrical energy.
• Here it’s the orientation  that’s changing to produce the changing magnetic
flux.
• Lenz’s law makes it hard to turn a generator that’s supplying electrical energy.
• That’s why we have to
burn fuels or use the
energies of water or
wind to generate electricity.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-11
Clicker question
•
A copper penny falls on a path that takes it between the
poles of a magnet. Does the penny hit the ground going
faster or slower than if the magnet were not present?
A. The penny will hit the ground going faster.
B. The penny will hit the ground going slower.
C. The penny will hit the ground going the same speed either
way.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-12
Clicker question
•
A copper penny falls on a path that takes it between the
poles of a magnet. Does the penny hit the ground going
faster or slower than if the magnet were not present?
A. The penny will hit the ground going faster.
B. The penny will hit the ground going slower.
C. The penny will hit the ground going the same speed either
way.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-13
Inductance
• Mutual inductance occurs when a
changing current in one circuit
results, via changing magnetic flux,
in an induced emf and thus a current
in an adjacent circuit.
• Mutual inductance occurs because some
of the magnetic flux produced by one
circuit passes through the other circuit.
• Self-inductance occurs when a
changing current in a circuit results
in an induced emf that opposes the
change in the circuit itself.
• Self-inductance occurs because some of
the magnetic flux produced in a circuit
passes through that same circuit.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-14
Clicker question
•
A long wire carries a current I as shown. What is the
direction of the current in the circular conducting loop
when I is decreasing?
A. The current flows counterclockwise.
B. The current flows clockwise.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-15
Clicker question
•
A long wire carries a current I as shown. What is the
direction of the current in the circular conducting loop
when I is decreasing?
A. The current flows counterclockwise.
B. The current flows clockwise.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-16
Self-inductance
• The self-inductance L of a circuit is defined as the ratio of
the magnetic flux through the circuit to the current in the
circuit:
 B  LI
• In differential form:
d B
dI
L
dt
dt
• Therefore, by Faraday’s law,
the emf across an inductor is
dI
EL   L
dt
• The minus sign shows that the direction
of the inductor emf is such as to oppose
the change in the inductor current.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-17
Clicker question
•
Current flows from left to right through the inductor as
shown. A voltmeter connected across the inductor gives
a constant reading, and shows that the left end is
positive. Is the current in the inductor changing, and if
so, how?
A. The current is increasing.
B. The current is decreasing.
C. The current is constant.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-18
Clicker question
•
Current flows from left to right through the inductor as
shown. A voltmeter connected across the inductor gives
a constant reading, and shows that the left end is
positive. Is the current in the inductor changing, and if
so, how?
A. The current is increasing.
B. The current is decreasing.
C. The current is constant.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-19
Magnetic energy
• As current builds up in an inductor, the inductor absorbs
energy from the circuit.
• That energy is stored in the inductor’s magnetic field.
• For an inductor, the stored energy is U B  12 LI 2 .
• Considering the uniform magnetic field inside a solenoid shows
that the magnetic energy density is
B2
uB 
2 0
• This is a universal expression: wherever there’s a magnetic
field, there’s energy with density B2/20.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-20
Induced electric fields
• The induced emf in a circuit subject to changing magnetic
flux results from an induced electric field.
• Induced electric fields result from changing magnetic flux.
• This is described by the full form of Faraday’s law, one of the four
fundamental laws of electromagnetism:
dB
O
 E  dr   dt
where the integral is taken around any closed loop, and where the flux is
through any area bounded by the loop.
• Loosely, Faraday’s law states that a changing magnetic field
produces an electric field.
• Thus not only charges but also changing magnetic fields are sources of
electric field.
• Unlike the electric field of a static charge distribution, the induced
electric field is not conservative.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-21
Static and induced electric fields
• Static electric fields begin and end on charges.
• But induced electric fields generally form closed loops.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-22
Summary
• Faraday’s law describes electromagnetic induction, most
fundamentally the phenomenon whereby a changing
magnetic field produces an electric field:
dB
O
 E  dr   dt
• This induced electric field is nonconservative and its field lines
have no beginnings or endings.
• In the presence of a circuit, the induced electric field gives rise
to an induced emf and an induced current.
• Lenz’s law states that the direction of the induced current is such that the
magnetic field it produces acts to oppose the change that gives rise to it.
• Self-inductance is a circuit property whereby changing current in a
circuit results in an induced emf that opposes the change.
• Consideration of current buildup in an inductor shows that all
magnetic fields store energy, with energy density B2/20.
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-23
Magnetic induction and Faraday’s law
Ch 27 Problem 40
A square wire loop with sides of 3.0 m is perpendicular to a
uniform magnetic field of 2.0 T. A 6.0 V light bulb is in
series with the loop. The magnetic field is reduced steadily
to zero over time ∆t.
(a)Find ∆t such that the light will shine at full brightness
during this time.
(b)Which way will the loop current flow?
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-24
(a) State Faraday’s law and Lenz’s law using words as well as
symbols. Explain all symbols that you use. [6]
(b) A small circular copper ring is inside a larger loop that is
connected to a battery and a switch as shown in the figure.
Use Lenz’s law to find the direction of the current induced in the
small ring
(i) just after switch S is closed,
(ii) after S has been closed a long time and
(iii) just after S has been reopened after being closed a long time.
[4]
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-25
Magnetic induction and Faraday’s law
Ch 27 Exercise 18
A conducting loop of area 240 cm2 and resistance 12 Ω lies at
right angles to a spatially uniform magnetic field. The loop
carries an induced current of 320 mA. At what rate is the
magnetic field changing?
Ch 27 Exercise 19
Both on Sheet 10
The magnetic field inside a 20 cm diameter solenoid is
increasing at a rate of 2.4 T/s. How many turns should a
coil wrapped around the outside of the solenoid have so
that the emf induced in the coil is 15 V?
Copyright © 2007 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Slide 27-26