* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Electromagnetism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Field (physics) wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Lorentz force wikipedia , lookup
Potential energy wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
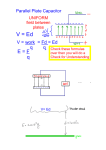
Electric potential at a point has no real significance, mainly because you have nothing to compare it to. You typically discuss the potential of a point relative to some other point of known potential. Therefore we usually look at the potential difference or voltage between two points. V VB VA V – electric potential difference or voltage (V) V – electric potential (V) We can now relate electric potential difference to electric field U V E ds q A B For a uniform electric field we can simplify the previous expression. cos = 1 when E and ds are parallel (same direction) B V E ds A B E cos ds A We can look at the scalar form of the dot product B Eds A B E ds Es B A Ed A d is the distance between point A and point B E A d B When the external electric field is applied above, a test positive charge will move from A to B. • At point A it has more potential energy and is therefore more likely to move to a point where it will have less potential energy. • Point A has a higher potential energy and hence a higher potential. • Point B has a lower potential energy and hence a lower potential. This is similar to dropping a mass in a gravitational field. The electric field ALWAYS points from a high potential to a low potential for a positive charge. V Ed The negative sign denotes that the potential is decreasing as you move from point A to point B. Work is done by the system. If you were moving the positive charge from point B to point A the sign would be positive. Work is done on the system. A d E B How would the electric potential change if you moved a charge from point A to point B perpendicular to the direction of an external electric field? The electric potential does not change. We are not moving the charge against a force and therefore no work is done. The potential energy does not change. This means that all points in a plane perpendicular to the direction of the electric field are at the same electric potential. A surface can be constructed from these point called an Equipotential Surface. Equipotential surface – all points on the surface are at the same electric potential. What would be the shape of the equipotential surface for a point charge? An electron is pushed into an electric field where it acquires a 1-V electrical potential. Suppose instead that two electrons are pushed the same distance into the same electric field. The electrical potential of the two electrons is 1. 0.25 V. 2. 0.5 V. 3. 1 V. 4. 2 V. 5. 4 V. V Ed Only depends on electric field strength and distance moved Example: A positive charge of 5 mC is placed near the positive plate of two parallel oppositely charged plates. The charge feels a force of 100 N. a) What is the strength of the electric field between the parallel plates? b) What is the potential difference between the parallel plates if they are separated by a distance of 2 cm? c) How much energy is required to move the positive charge back to the positive plate? d) How much energy is required to move the charge from the top of the positive plate to the bottom of the positive plate? E F 7 N 2 x10 q C a) F qE b) V Ed 4 x105V c) U V q d) U q V 0 E U qV = 2J Ed We looked at the electric potential for any electric field. Now let us examine a specific electric field source – a point charge. Let us begin with our general expression for potential difference, and the expression for the electric field of a point charge. B V VB VA E ds E A ke q V VB VA 2 r A rˆ ds B ke q r 2 rˆ rˆ ds 1 ds cos dr Projection of ds onto direction of r When we look at electric potential of a point charge the sign of the charge is important, since we do not have a direction to consider. B 1 ke q V 2 dr ke q r r A A B If we choose the following reference voltage: VA 0 at rA 1 1 VB VA ke q rB rA ke q VB rB ke q V r Electric potential due to a point charge • The electric potential is a scalar quantity. This means we do not have any direction to consider when determining the net electric potential at a point. • This often makes using electric potential more convenient than using the electric field. Only scalar quantities – no directional components to work with. The net electric potential is given by: qi V ke i ri The close relationship between electric potential and electric potential energy allows us to look at the electric potential energy stored by a system of point charges based on knowledge of their electric potential. • A charge that is moved from infinity to a position in space in the absence of an electric field requires no energy. • A second charge moved from infinity to a position a distance r1 from the first charge requires work to be done against the electric field of the first charge and hence energy is stored in the system. • A third charge moved from infinity to a position a distance r1 from the first charge and r2 from the second charge requires work to be done against the net electric field due to both charges and hence energy is stored in the system. r12 q1 q2 r13 r23 q3 We can bring charge q1 in from infinity without changing the energy of the system. U1 = 0 We must do work to bring in charge q2. The total energy required to support this configuration can be determined as follows: ke q1 q2 r 12 U U1 U 2 0 q2V1 We must do additional work to bring in charge q3. We can determine the total energy required for this configuration in a similar manner. U U1 U 2 U 3 0 q2V1 q3V1 q3V2 q2 ke q1 q3 ke q1 q3 ke q2 r r 12 r13 23