* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Charges in a Magnetic Field
Double-slit experiment wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Photoelectric effect wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Standard Model wikipedia , lookup
Renormalization wikipedia , lookup
Electric charge wikipedia , lookup
Magnetic monopole wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Charges in a Magnetic Field An electron entering a magnetic field experiences a force similar to that on a wire. A proton would experience a force in the opposite direction. Since we have F = IlB, and I = q , t then we can substitute so we get F = qlB , t and l =v t Then, the force on a proton or electron, or any charged particle is: F = qvB Practice Problem: What is the force on a proton moving at 2.0 x 106 m/s in a magnetic field of 0.5 Tesla. F = qvB q = 1.6 x 10-19 C v = 2.0 x 106 m/s B = 0.5 T F = (1.6 x 10-19 C)(2.0 x 106 m/s)(0.5T) F = 1.6 x 10-13 N Since a particle is free to move, upon entering a magnetic field, it will constantly change directions in response to the force, and it moves in a circle. proton + electron Magnetic field out of page Mass Spectrometry A practical application of this, is a device known as a mass spectrometer, which uses the charge to mass ratio of ions to determine the masses of particles. By measuring the speed of the particles and the radius of the path, we can use F = qvB , and, Fc = mv2 r then, qvB = mv2 r And we get, q = v m Br If the charge on the particle is known, the mass can be calculated. A Little History • In 1897, J.J. Thomson found the charge to mass ration (q/m) for an electron. • Between 1909-1913, Robert Millikin found the charge for an electron using his oil drop experiment. • From this charge, the mass of the electron could be calculated using Thomson’s ratio. Electron Beams An electron beam can be created through thermionic emission. An electron beam is generated when a filament is heated until it emits electrons. Once they are emitted, the electrons are controlled by electric and magnetic fields. Devices such as computer monitors, television tubes, and cathode ray tubes create electron beams. A cathode ray tube is an evacuated glass tube with an electron source at one end, a screen at the other, and controlling plates and magnets in between.


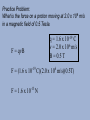






![NAME: Quiz #5: Phys142 1. [4pts] Find the resulting current through](http://s1.studyres.com/store/data/006404813_1-90fcf53f79a7b619eafe061618bfacc1-150x150.png)










