Download Document

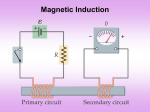
General Physics (PHY 2140)
Lecture 9
 Electricity and Magnetism
Induced voltages and induction
 Magnetic flux and induced emf
 Faraday’s law
Motional EMF
Lenz’s Law
Applications
Self-Inductance
RL Circuits (maybe)
http://www.physics.wayne.edu/~alan/2140Website/Main.htm
Chapter 20
5/25/2017
1
Lightning Review
Last lecture:
1. Magnetism
 Application of magnetic forces
B l  o I
 Ampere’s law
 Current loops and solenoids
  B A  BA cos 
2. Induced voltages and induction
 Magnetic flux
Review Problem: A rectangular loop is placed in a

uniform magnetic field with the plane of the loop
parallel to the direction of the field. If a current is made
to flow through the loop in the sense shown by the
arrows, the field exerts on the loop:
1. a net force.
2. a net torque.
3. a net force and a net torque.
4. neither a net force nor a net torque.
5/25/2017
Recall:
F  qvB sin 
2
Magnetic Field of a current loop
Magnetic field produced by a wire can be enhanced
by having the wire in a loop.
x1
B
I
x2
5/25/2017
3
Solenoid Magnet
Field lines inside a solenoid magnet are parallel, uniformly spaced
and close together.
The field inside is uniform and strong.
The field outside is non uniform and much weaker.
One end of the solenoid acts as a north pole, the other as a south
pole.
For a long and tightly looped solenoid, the field inside has a value:
B  o nI
5/25/2017
4
Solenoid Magnet
B  o nI
n = N/l : number of (loop) turns per unit length.
I : current in the solenoid.
o  4 10 Tm / A
7
5/25/2017
5
Chapter 20: Introduction
Previous chapter: electric currents produce magnetic
fields (Oersted’s experiments)
Is the opposite true: can magnetic fields create electric
currents?
5/25/2017
6
20.1 Induced EMF and magnetic flux
Definition of Magnetic Flux
Just like in the case of electric flux,
consider a situation where the magnetic
field is uniform in magnitude and
direction. Place a loop in the B-field.
The flux, , is defined as the product of
the field magnitude by the area crossed
by the field lines.
  Bperp A  BA cos
where B perp is the component of B
perpendicular to the loop,  is the angle
between B and the normal to the loop.
Units: T·m2 or Webers (Wb)
5/25/2017
The value of magnetic flux is proportional to the total number of
magnetic field lines passing through the loop.
7
Problem: determining a flux
A square loop 2.00m on a side is placed in a magnetic field of
strength 0.300T. If the field makes an angle of 50.0° with the
normal to the plane of the loop, determine the magnetic flux
through the loop.
5/25/2017
8
A square loop 2.00m on a side is placed in a magnetic field of strength 0.300T. If the
field makes an angle of 50.0° with the normal to the plane of the loop, determine the
magnetic flux through the loop.
Solution:
Given:
From what we are given, we use
L = 2.00 m
B = 0.300 T
 = 50.0˚
  BA cos   0.300T  2.00m  cos 50.0
2
 0.386 Tm2
Find:
=?
5/25/2017
9
20.1 Induced EMF and magnetic flux
Faraday’s experiment
Picture © Molecular Expressions
5/25/2017
Two circuits are not connected:
no current?
However, closing the switch
we see that the compass’
needle moves and then goes
back to its previous position
Nothing happens when the
current in the primary coil is
steady
But same thing happens when
the switch is opened, except
for the needle going in the
opposite direction…
What is going on?
10
20.2 Faraday’s law of induction
Induced current
I
5/25/2017
v
S
N
11
20.2 Faraday’s law of induction
I
v
B
S
I
N
B
I
5/25/2017
v
A current is set up in the circuit as long as
there is relative motion between the magnet
and the loop.
12
Does there have to be motion?
I
(induced) I
-
+
AC Delco
1 volt
5/25/2017
13
Does there have to be motion?
I
-
+
AC Delco
1 volt
5/25/2017
14
Does there have to be motion?
I
(induced)
-
+
AC Delco
1 volt
5/25/2017
15
Does there have to be motion?
NO!!
-
+
AC Delco
1 volt
5/25/2017
16
Maybe the B-field needs to change…..
B
5/25/2017
v
17
Maybe the B-field needs to change…..
I
B
5/25/2017
v
18
Maybe the B-field needs to change…..
I
I
v
B
5/25/2017
I
19
Faraday’s law of magnetic induction
In all of those experiment induced EMF is caused by a change in the
number of field lines through a loop. In other words,
The instantaneous EMF induced in a circuit equals the rate of change
of magnetic flux through the circuit.
E
Lenz’s law

N
t
The number of loops matters
Lenz’s Law: The polarity of the induced emf is such that it produces a
current whose magnetic field opposes the change in magnetic flux
through the loop. That is, the induced current tends to maintain the
original flux through the circuit.
5/25/2017
20
Applications:
Ground fault interrupter
Electric guitar
SIDS monitor
Metal detector
…
5/25/2017
21
Example : EMF in a loop
A wire loop of radius 0.30m lies so that an external magnetic field
of strength +0.30T is perpendicular to the loop. The field changes
to -0.20T in 1.5s. (The plus and minus signs here refer to opposite
directions through the loop.) Find the magnitude of the average
induced emf in the loop during this time.
B
5/25/2017
22
A wire loop of radius 0.30m lies so that an external magnetic field of strength
+0.30T is perpendicular to the loop. The field changes to -0.20T in 1.5s. (The
plus and minus signs here refer to opposite directions through the loop.) Find
the magnitude of the average induced emf in the loop during this time.
Given:
r = 0.30 m
Bi = 0.30 T
Bf = -0.20 T
t = 1.5 s
The loop is always perpendicular to the field, so the
normal to the loop is parallel to the field, thus cos = 1.
The flux is then
  BA  B r 2
Initially the flux is
 i   0.30T    0.30m  = 0.085 T  m 2
2
Find:
EMF=?
and after the field changes the flux is
 f   0.20T    0.30m  = -0.057 T  m 2
2
The magnitude of the average induced emf is:
  f  i 0.085 T  m2 -(-0.057 T  m 2 )
emf 


 0.095V
t
t
1.5s
5/25/2017
23
Example 2: EMF of a flexible loop
The flexible loop in figure below has a radius of 12cm and is in a magnetic
field of strength 0.15T. The loop is grasped at points A and B and stretched
until it closes. If it takes 0.20s to close the loop, find the magnitude of the
average induced emf in it during this time.
X
X
A
X
X
X
X
X
X
X
X
X
X
X
X
X
X
B
ΔΦ = BA = 0.15T × π (0.12 m)2 = 0.0068 T∙m2
Δt = 0.20 s Then, emf = ΔΦ/ Δt = 0.034 V
emf = 0.034 V
5/25/2017
24
20.3 Motional EMF
l
B
v
F
Let's consider a conducting bar moving perpendicular to a uniform
magnetic field with constant velocity v.
F  qvB sin 
This force will act on free charges in the conductor. It will tend to
move negative charge to one end, and leave the other end of the bar
with a net positive charge.
5/25/2017
25
Motional EMF
The separated charges will create an electric field which
will tend to pull the charges back together.
When equilibrium exists, the magnetic force, F=qvB, will
balance the electric force, F=qE, such that a free charge
in the bar will feel no net force.
(recall our velocity selector example)
Thus, at equilibrium, E = vB. The potential difference
across the ends of the bar is given by V=El or
V  El  Blv
A potential difference is maintained across the conductor
as long as there is motion through the field. If the motion
is reversed, the polarity of the potential difference is also
reversed.
5/25/2017
26
Motional EMF – conducting rails
R
x
B
v
We can apply Faraday's law to the complete loop. The change of flux through
the loop is proportional to the change of area from the motion of the bar:
  BA  Blx
5/25/2017
current
I
or (Faraday’s law)
E Blv

R
R

x
E
 Bl
 Blv
t
t
Motional EMF
27
Example: wire in the magnetic field
Over a region where the vertical component of the Earth's magnetic field is
40.0µT directed downward, a 5.00 m length of wire is held in an east-west
direction and moved horizontally to the north with a speed of 10.0 m/s.
Calculate the potential difference between the ends of the wire, and
determine which end is positive.
EMF = Blv = 40.0 µT × 5.00 m × 10.0 m/s = 0.002 V
Use right hand rule and F = qv × B to determine the polarity.
Answer: west end is positive.
5/25/2017
28
20.4 Lenz’s law revisited
Application of Lenz's law will tell
us the direction of induced
currents, the direction of
applied or produced forces,
and the polarity of induced
emf's.
Lenz's law says that the induced current will produce
magnetic flux opposing this change. To oppose an
increase into the page, it generates magnetic field which
points out of the page, at least in the interior of the loop.
Such a magnetic field is produced by a counterclockwise
current (use the right hand rule to verify).
5/25/2017
29
Lenz’s law: energy conservation
We arrive at the same conclusion from
energy conservation point of view
The preceding analysis found that the
current is moving ccw. Suppose that this
is not so.

If the current I is cw, the direction of the
magnetic force, BlI, on the sliding bar



5/25/2017
would be right.
This would accelerate the bar to the right,
increasing the area of the loop even more.
This would produce even greater force
and so on.
In effect, this would generate energy out of
nothing violating the law of conservation of
energy.
Our original
assertion that the
current is cw is
not right, so the
current is ccw!
30
S
S
v
The induced
flux seeks to
counteract
the change.
N
induced
change
5/25/2017
S
S
N v
N
induced
change
31
Example: direction of the current
Find the direction of the current induced in
the resistor at the instant the switch is
closed.
Induced
current
B
5/25/2017
32
Applications of Magnetic Induction
Tape / Hard Drive / ZIP Readout

Tiny coil responds to change in flux as the magnetic domains (encoding
0’s or 1’s) go by.
Question: How can your VCR display an image while paused?
Credit Card Reader

–
Must swipe card
 generates changing flux
Faster swipe  bigger signal
5/25/2017
33
20.5 Generators
Generators and motors are two of the most important
applications of induced emf (magnetic inductance).
A generator is something that converts mechanical
energy to electrical energy.
Alternating Current (AC) generator
Direct Current (DC) generator
A motor does the opposite, it converts electrical energy
to mechanical energy.
5/25/2017
34
AC generator
D
C
l
a
Compute EMF


It is only generated in BC
and DA wires
EMF generated in BC and
DA would be
EBC  EDA  Blv perp

A
B
v sin 
B
v
θ
Thus, total EMF is
E  2 Blv perp  2 Blv sin 

If the loop is rotating with w
a 
E  2 Blv sin wt  2 Bl  w  sin wt
2 
5/25/2017
A
as v=rw=aw/2
and  = wt
35
AC generator (cont)
Generalize the result to N loops
E  NBAw sin wt
EMF generated by the AC generator
where we also noticed that A=la
Emax  NBAw is
Note:
reached when wt=90˚ or 270˚ (loop
parallel to the magnetic field)
5/25/2017
36
DC generator
By a clever change to the rings and brushes of the ac
generator, we can create a dc generator, that is, a
generator where the polarity of the emf is always
positive. The basic idea is to use a single split ring
instead of two complete rings. The split ring is arranged
so that, just as the emf is about to change sign from
positive to negative, the brushes cross the gap, and the
polarity of the contacts is switched. The polarity of the
contacts changes in phase with the polarity of the emf -the two changes essentially cancel each other out, and
the emf remains always positive. The emf still varies
sinusoidally during each half cycle, but every half cycle is
a positive emf.
5/25/2017
37
DC Generator
5/25/2017
38
Motors
A motor is basically a generator running in reverse. A
current is passed through the coil, producing a torque
and causing the coil to rotate in the magnetic field. Once
turning, the coil of the motor generates a back emf, just
as does the coil of a generator. The back emf cancels
some of the applied emf, and limits the current through
the coil.
5/25/2017
39
Example: coil in magnetic field
A coil of area 0.10 m² is rotating at 60 rev/s with its axis of rotation
perpendicular to a 0.20T magnetic field. (a) If there are 1000 turns on
the coil, what is the maximum voltage induced in the coil? (b) When the
maximum induced voltage occurs, what is the orientation of the coil
with respect to the magnetic field?
E  NBAw sin wt
Recall: w  2 f
1000(0.20)(0.10)(260) = 7540 V
Max when loop parallel to the magnetic field.
5/25/2017
40
Eddy currents (application)
Magnetic Levitation (Maglev) Trains

Induced surface (“eddy”) currents produce field in opposite direction
 Repels magnet
 Levitates train
S
N
“eddy” current


rails
Maglev trains today can travel up to 310 mph
 Twice the speed of Amtrak’s fastest conventional train!
May eventually use superconducting loops to produce B-field
5/25/2017

No power dissipation in resistance of wires!
41
20.6 Self-inductance
When a current flows through a loop, the magnetic field
created by that current has a magnetic flux through the
area of the loop.
If the current changes, the magnetic field changes, and
so the flux changes giving rise to an induced emf. This
phenomenon is called self-induction because it is the
loop's own current, and not an external one, that gives
rise to the induced emf.
Faraday’s law states

E  N
t
5/25/2017
42
The magnetic flux is proportional to the magnetic field,
which is proportional to the current in the circuit
Thus, the self-induced EMF must be proportional to the
time rate of change of the current
I
E  L
t
where L is called the inductance of the device
Units: SI: henry (H)
If flux is initially zero,
5/25/2017
1 H  1V  s
A
 N 
LN

I
I
43
Example: solenoid
A solenoid of radius 2.5cm has 400 turns and a length of 20 cm. Find
(a) its inductance and (b) the rate at which current must change
through it to produce an emf of 75mV.
N
B  0 nI  0 I
l
NB
N2A
L
 0
I
l
E  L
5/25/2017
I
I
E


t
t
L
N
 B  BA   0 IA
l
= (4 x 10-7)(160000)(2.0 x 10-3)/(0.2) = 2 mH
= -(75 x 10-3)/ (2.0 x 10-3) = 37.5 A/s
44
Inductor in a Circuit
Inductance can be interpreted as a measure of opposition to the rate
of change in the current

Remember resistance R is a measure of opposition to the current
As a circuit is completed, the current begins to increase, but the
inductor produces an emf that opposes the increasing current


Therefore, the current doesn’t change from 0 to its maximum
instantaneously
Maximum current:
I max
5/25/2017
E

R
45
20.7 RL Circuits
Recall Ohm’s Law to find the voltage drop on R
V  IR
(voltage across a resistor)
We have something similar with inductors
I
EL   L
t
(voltage across an inductor)
Similar to the case of the capacitor, we get an equation
for the current as a function of time (series circuit).

E
 Rt / L
I  1 e
R
5/25/2017

L

R
46
RL Circuit (continued)

V
 Rt / L
I  1 e
R
5/25/2017

47
20.8 Energy stored in a magnetic field
The battery in any circuit that contains a coil has to do
work to produce a current
Similar to the capacitor, any coil (or inductor) would store
potential energy
1 2
PEL  LI
2
Summary of the properties of circuit elements.
5/25/2017
Resistor
Capacitor
Inductor
units
ohm, W = V / A
farad, F = C / V
henry, H = V s / A
symbol
R
C
L
relation
V=IR
Q=CV
emf = -L (I / t)
power dissipated
P = I V = I² R = V² /
R
0
0
energy stored
0
PEC = C V² / 2
PEL = L I² / 2
48
Example: stored energy
A 24V battery is connected in series with a resistor and an inductor,
where R = 8.0W and L = 4.0H. Find the energy stored in the inductor
(a) when the current reaches its maximum value and (b) one time
constant after the switch is closed.
5/25/2017
49