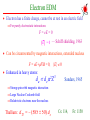* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Precision atomic physics tests of P, CP, and CPT symmetries
Quantum chromodynamics wikipedia , lookup
Magnetic monopole wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Atomic nucleus wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
History of quantum field theory wikipedia , lookup
Antiproton Decelerator wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Scalar field theory wikipedia , lookup
Electron scattering wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Nuclear structure wikipedia , lookup
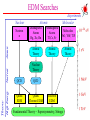
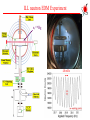
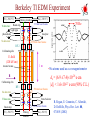
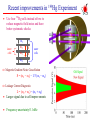
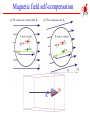
I Fundamental Symmetry Tests with Atoms Michael Romalis Princeton University I 1. Atomic Parity Violation 2. Limits on CP violation from Electric Dipole Moments 3. Tests of CPT and Lorentz symmetries Atomic parity violation Parity transformation: ri ri Electromagnetic forces in an atom conserve parity [Hatomic, P]=0 Atomic stationary states are eigenstates of Parity But weak interactions maximally violate Parity! Electromagnetic Weak Tiny virtual contribution of Z-boson exchange can be measured! I Atomic Parity Violation Experiments Early work: M.-A. Bouchiat, C. Bouchiat (Paris) Sandars (Oxford) Khriplovich, Barkov, Zolotorev (Novosibirsk) Fortson (Seattle) Current Best Measurement – Wieman (Bolder, 1999) Parity mixing on M1 transition 6S1/2 7S1/2 transition in Cs Experimental accuracy on PV amplitude EPV: 0.35% I I Relation to Standard Model Parameters Exchange of virtual Z0 boson: HW GF e 5e C1u u u C1d d d ... 2 GF H [ N Z (1 4 sin W )] 5 (r) 8 e W 2 Weak charge Qw Nuclear (neutron) distribution EPV k PV QW Best Atomic Calculation in Cs: 0.27% error - Derevianko (Reno, 2009) Phys. Rev. Lett. 102, 181601 (2009) Parity violation in Yb Parity violation is enhanced 100 times in Yb because of close opposite-parity states (DeMille, 1995) Atomic calculations will not be as accurate, but one can compare a string of isotopes and measure the anapole moment First observation by Budker with 14 % accuracy (2009) The experiment is improving, needs to reach ~ 1% K. Tsigutkin et al, Phys. Rev. Lett. 103, 071601 (2009) I Impact on Electroweak Physics I T and CP violation by a permanent EDM Time Reversal: I t–t I –I dd I d –d 0 d =dI I d 0 violation of time reversal symmetry Vector: CPT theorem also implies violation of CP symmetry EDM T violation CP violation • Relativistic form of interaction: L = d E = – i d 5F 2 Requires a complex phase I I EDM Searches Nuclear High Energy Theory Nuclear Atomic Neutron n Experiments Molecular Atomic Diamagnetic Atoms Hg, Xe, Rn Paramagnetic Atoms Tl,Cs, Fr Molecules PbO, YbF, TlF Atomic Theory Atomic Theory Atomic Theory Nuclear Theory QCD QCD Quark EDM Quark Chromo-EDM Electron EDM Fundamental Theory Supersymmetry, Strings Discovery potential of EDMs In SM the only source of CP violation is a phase in CKM matrix The EDMs are extremely small, require high-order diagrams with all 3 generations of quarks Almost any extension of the Standard Model contains additional CPviolating phases that generally produce large EDMs. Raw energy sensitivity: d ~ em , 10 – 27 e cm 2 =100 TeV Current experiments are already sensitive enough to constrain EDMs from Supersymmetry by a factor of 100 or more Baryogenesis scenarios: Electroweak baryogenesis: EDMs around the corner, somewhat unfavorable based on existing constraints Leptogenesis: No observable EDMs Other (GUT scale, CPT violation): No observable EDMs I I Experimental Detection of an EDM • Measure spin-precession frequencies B E d w1 w1 = B 2 B+ 2dE h E H = – B – d E d w1 w2 = 2 B 2dE h w1 – w2 = 4dE h • Statistical Sensitivity: Single atom with coherence time t: dw = t1 h N uncorrelated atoms measured for time T >> t: d d = 1 2E 2tTN Search for EDM of the neutron Historically, nEDM experiments eliminated many proposals for CP violation I I ILL neutron EDM Experiment n, 199Hg 40 mHz I Recent nEDM result Complicated effects of motional magnetic field Bm = E v/c Random motion results in persistent rotating magnetic field Dependance on field gradient dBz/dz dBr/dr r V V Rotating field causes frequency shift E and B0 into page dBz/dz dn = 0.61.5(stat)0.8(syst) 10-26 ecm |dn| < 3.0 10-26 ecm (90% CL) Factor of 2 improvement dBz/dz C.A. Baker et al Phys. Rev. Lett. 97, 131801 (2006) I Cryogenic nEDM experiments Superthermal production in superfluid 4He N increased by 100 – 10000 He-4 good isolator, low temperature E increased by 5 Superconducting magnetic shields SQUID magnetometers 1 m I Electron EDM Electron has a finite charge, cannot be at rest in an electric field For purely electrostatic interactions F = eE = 0 E = 0 — Schiff shielding, 1963 Can be circumvented by magnetic interactions, extended nucleus F = eE+B = 0, E 0 Enhanced in heavy atoms: 3 2 d a d e Z Strong spin-orbit magnetic interaction Large Nuclear Coulomb field Relativistic electrons near the nucleus Thallium: d Tl = – (585 ± 50) d e Sandars, 1965 Cs: 114, Fr: 1150 I Berkeley Tl EDM Experiment Tl (~700 C) Tl detectors Mixing chamber Beam stop Light pipe photodiodes Na (~350 C) 378 nm laser beams 70 Hz Analyzer Na detectors 590 nm laser beams RF 2 Collimating slits E-field (120 kV/cm) 1m Atomic beams B Collimating slits RF 1 590 nm laser beams • Na atoms used as a co-magnetometer de = (6.9 7.4)10-28 ecm |de| < 1.610-27 ecm (90% C.L.) Na detectors State Selector Tl detectors 378 nm laser beams Beam stop Tl (~700 C) Mixing chamber Na (~350 C) B. Regan, E. Commins, C. Schmidt, D. DeMille, Phys. Rev. Lett. 88, 071805 (2002) YbF Experiment Polarized polar molecules have very high internal electric field It is hard to generate paramagnetic molecules New Result !!! de= (−2.4 ± 5.7 ± 1.5) × 10−28e cm Only 20% better than Thallium J. J. Hudson, D. M. Kara, I. J. Smallman, B. E. Sauer, M. R. Tarbutt, E. A. Hinds, Nature 473, 493, (2011) I 199Hg EDM Experiment Solid-state Quadrupled UV laser 100,000 hours of operation High purity non-magnetic vessel Hg Vapor cells All materials tested with SQUID Spin coherence time: 300 sec Electrical Resistance: 21016 W I Recent improvements in 199Hg Experiment Use four 199Hg cells instead of two to reduce magnetic field noise and have better systematic checks inner cells w1 w2 w3 E E outer cells w4 Magnetic Gradient Noise Cancellation S = w2 w3 1/3 w1 w4 Leakage Current Diagnostic L = w2 w3 w1 w4 Larger signal due to cell improvements Frequency uncertainty 0.1 nHz I New 199Hg EDM Result I About 1 year of data Changed all components of the system: d(199Hg) = (0.49±1.29stat±0.76syst)×10−29 e cm W. C. Griffith, M. D. 199 −29 |d( Hg)| < 3.1×10 e cm (95% C.L.) Swallows, T. H. Loftus, M. V. Romalis, B. R. Factor of 7 improvement Heckel, E. N. Fortson Phys. Rev. Lett. 102, 101601 (2009) Continued work on 199Hg Still a factor of 10-20 away from shot noise limit Limited by light shift noise, magnetic shield noise Need to find more precisely path of leakage currents Practical cell fabrication issues Steady improvement – factor of 3-5 improvement in ~3 years I I Interpretation of nuclear EDM Limits No atomic EDM due to EDM of the nucleus Schiff’s Theorem Electrons screen applied electric field d(Hg) is due to finite nuclear size nuclear Schiff moment S Difference between mean square radius of the charge distribution and electric dipole moment distribution 2 x 2 x 5 r 2 3 S dx x 5 3 x ch I E Recent work by Haxton, Flambaum on form of Schiff moment operator Schiff moment induces parity mixing of atomic states, giving an atomic EDM: da = RA S RA - from atomic wavefunction calculations, uncertainty 50% B. P. Das et al, V. Dzuba et al. I Interpretation of nuclear EDMs The Schiff moment is induced by CP nucleon-nucleon interaction: Due to coherent interactions between the valence nucleon and the core S RN gNN Large uncertainties due to collective effects gNN n p Engel, Flambaum CP-odd pion exchange dominated by chromo-EDMs of quarks g Factor of 2 uncertainty in overall coefficient due to approximate cancellation q (1) gNN ~ ~ RQCD ( du dd ) Other effects: nucleon EDMs, electron EDM, CPviolating nuclear-electron exchange q Pospelov et al. Sen’kov Oshima Flambaum I Jon Engel calculations for 199Hg(2010) isovector I Octupole Enhancement I 1| 1|/2 |+ DE I | |/2 P, T | |/2 1| 1|/2 | V PT Slab ~ e Z A2/3 2 32/DE Sintr ~ eZA23 DE ~ 3 A1 / 3 DE 2 , 3 ~0.1 Haxton & Henley; Auerbach, Flambaum & Spevak; Hayes, Friar & Engel; Dobaczewski & Engel 223Rn t1/2 I Deth (keV) DEexp (keV) 105 S (efm3) 1028 dA (e cm) 23.2 m 7/2 37 -1000 2000 223Ra 11.4 d 3/2 170 50.2 400 2700 225Ra 14.9 d 1/2 47 55.2 300 2100 223Fr 22 m 3/2 75 160.5 500 2800 225Ac 10.0 d 3/2 49 40.1 900 229Pa 1.5 d 5/2 5 0.22 12000 199Hg 129Xe 1/2 1/2 -1.4 -5.6 1.75 0.8 I Oven: 225Ra EDM measurement with 225Ra Transverse cooling Zeeman Slower Statistical uncertainty: Magneto-optical trap 100 days 10 days 100 kV/cm 100 10 s 1064 10% -26 e cm Phase II dd = 3 x 10-28 • 225Ra / 199Hg enhance factor ~ 1,000 • dd(199Hg) = 1.5 x 10-29 e cm EDM measurement Optical dipole trap I Limits on EDMs of fundamental particles EDM: e d – d < 610 – 27 e cm d u • Neutron EDM: e(d d +0.5d u)+1.3d d –0.32d u <310 –26 e cm • Electron EDM: d e < 3 10 – 26 m e e cm d~m md • 199Hg Atom New 199Hg Limit CMSSM m1/2 = 250 GeV m0 = 75 GeV tan = 10 New limits on ,A K.A. Olive, M. Pospelov, A. Ritz, and Y. Santoso, PRD 72, 075001 (2005) I More recent EDM Analysis Electron, neutron and Hg limits provide complimentary constraints for some, but not all, possible CPviolating phases Y. Li, S. Profumo, and M. Ramsey-Musolf, JHEP08(2010)062 I On to breaking more symmetries … Started with P, C, T symmetries Each symmetry violation came as a surprise Parity violation weak interactions CP violation Three generations of quarks In each case symmetry violations were found before corresponding particles could be produced directly CPT symmetry is a unique signature of physics beyond quantum field theory. Provides one of few possible ways to access Quantum Gravity effects experimentally. I A theoretical framework for CPT and Lorentz violation I Introduce an effective field theory with explicit Lorentz violation Fermions: – = (m + a + b ) + 5 L i + d 5 ) 2 ( + c a,b - CPT-odd c,d - CPT-even Alan Kostelecky a,b,c,d are vector fields in space with non-zero expectation value Vector and tensor analogues to the scalar Higgs vacuum expectation value Surprising bonus: incorporates CPT violation effects within field theory Greenberg: Cannot have CPT violation without Lorentz violation (PRL 89, 231602 (2002) Although see arXiv:1103.0168 CPT-violating interactions break Lorentz symmetry, give anisotropy signals Can search for CPT violation without the use of anti-particles In contrast, scalar properties of anti-particles (masses, magnetic moments) are likely to be the same I Phenomenology of Lorentz/CPT violation Modified dispersion relations: E2 = m2 + p2 + h p3 Jacobson Amelino-Cameli 2 Dimention-5 operator: L 5k (n ) Myers, Pospelov, Sudarsky n - preferred direction, k ~ h/Mpl Applied to fermions: H = h m2/MPl S·n Non-commutativity of space-time: [x,x] = L (F)(F F) Spin coupling to preferred direction Witten, Schwartz - a tensor field in space, [] 1/E2 Interaction inside nucleus: NN eijkjkSi Pospelov,Carroll I Spin Lorentz violation Spin coupling: L = – b 5 = – 2b ·S c.f. CPT-violating interaction Experimental Signatures L e A ge B S 2m Magnetic moment interaction b is a (four-)vector field permeating all space Vector interaction gives a sidereal signal in the lab frame Don’t need anti-particles to search for CPT violation Need a co-magnetometer to distinguish from regular magnetic fields Assume coupling is not in proportion to the magnetic moment h1= 21 B + 21 (b·nS) h2= 22 B + 22 (b·nS) 1 2 2 1 2 (b n S ) 1 2 h 1 2 nS – direction of spin sensitivity in the lab b I K-3He Co-magnetometer 1. Optically pump potassium atoms at high density (1013-1014/cm3) 2. 3He nuclear spins are polarized by spin-exchange collisions with K vapor 3. Polarized 3He creates a magnetic field felt by K atoms 8 B K = 3 k 0 M He 4. Apply external magnetic field Bz to cancel field BK K magnetometer operates near zero magnetic field 5. At zero field and high alkali density K-K spinexchange relaxation is suppressed 6. Obtain high sensitivity of K to magnetic fields in spin-exchange relaxation free (SERF) regime Turn most-sensitive atomic magnetometer into a co-magnetometer! J. C. Allred, R. N. Lyman, T. W. Kornack, and MVR, PRL 89, 130801 (2002) I. K. Kominis, T. W. Kornack, J. C. Allred and MVR, Nature 422, 596 (2003) T.W. Kornack and MVR, PRL 89, 253002 (2002) T. W. Kornack, R. K. Ghosh and MVR, PRL 95, 230801 (2005) Magnetic field self-compensation I Co-magnetometer Setup Simple pump-probe arrangement Measure Faraday rotation of fardetuned probe beam Sensitive to spin coupling orthogonal to pump and probe Details: Ferrite inner-most shield 3 layers of -metal Cell and beams in mtorr vacuum Polarization modulation of probe beam for polarimetry at 10-7rad/Hz1/2 Whole apparatus in vacuum at 1 Torr I Rotating K-3He Rotate – stop – measure – rotate Fast transient response crucial Record signal as a function of magnetometer orientation W b eff Have we found Lorentz violation? Pz eW y 1 1 S R e n co-magnetometer I Recording Sidereal Signal Measure in North - South and East - West positions Rotation-correlated signal found from several 180° reversals Different systematic errors Any sidereal signal would appear out of phase in the two signals I Long-term operation of the experiment N-S signal riding on top of Earth rotation signal, I 20 days of non-stop running with minimal intervention Sensitive to calibration E-W signal is nominally zero Sensitive to alignment Fit to sine and cosine waves at the sidereal frequency Two independent determinations of b components in the equatorial plane bX YEW ; bX XNS / sin S EW XEW cos(2t ) YEW sin( 2t ) C EW bY XEW ; bY YNS / sin S NS XNS cos(2t ) YNS sin( 2t ) C NS I Final results Anamolous magnetic field constrained: xHexe = 0.001 fT ± 0.019 fTstat ± 0.010 fTsys yHeye = 0.032 fT ± 0.019 fTstat ± 0.010 fTsys J. M. Brown, S. J. Smullin, T. W. Kornack, and M. V. R., Phys. Rev. Lett. 105, 151604 (2010) Systematic error determined from scatter under various fitting and data selection procedures Frequency resolution is 0.7 nHz Anamalous electron couplings be are constrained at the level of 0.002 fT by torsion pendulum experiments (B.R. Heckel et al, PRD 78, 092006 (2008).) 3He nuclear spin mostly comes from the neutron (87%) and some from proton (5%) Friar et al, Phys. Rev. C 42, 2310 (1990) and V. Flambaum et al, Phys. Rev. D 80, 105021 (2009). bxn = (0.1 ± 1.6)1033 GeV byn = (2.5 ± 1.6)1033 GeV |bnxy| < 3.7 1033 GeV at 68% CL Previous limit |bnxy| = (6.4 ± 5.4) 1032 GeV D. Bear et al, PRL 85, 5038 (2000) 199 Improvement in spin anisotropy limits I Recent compilation of Lorentz-violation limits 1033 GeV I Many new limits in last 10 years Natural size for CPT violation ? m2 b ~h M pl m - fermion mass or SUSY breaking scale Existing limits: h ~ 109 1012 1/Mpl effects are already quite excluded V.A. Kostelecky and N. Russell arXiv:0801.0287 v4 Fine-tuning ? Possible explanation for lack Lorentz violation With Supersymmetry, dimension 3 and 4 Lorentz violating operators are not allowed Higher dimension operators are allowed Dimention-5 operators (e.g.L 5h (n )2 ) are CPTviolating, suppressed by MSUSY/MPlanck and are already quite constrained If CPT is a good symmetry, then the dimention-6 operators are the lowest order allowed Dimention-6 operators suppressed by (MSUSY/MPlank)2 ~10-31-10-33, still not significantly constrained, could be the lowest order at which Lorentz violation appears Pospelov, Mattingly I I CPT-even Lorentz violation L = – (m + a + b 5 ) + i + d 5 ) 2 ( + c Maximum attainable particle velocity vMAX c(1 c00 c0 j vˆj c jk vˆj vˆk a,b - CPT-odd c,d - CPT-even Coleman and Glashow Jacobson ) Implications for ultra-high energy cosmic rays, Cherenkov radiation, etc Many laboratory limits (optical cavities, cold atoms, etc) Models of Lorentz violation without breaking CPT: Doubly-special relativity Horava-Lifshitz gravity Something special needs to happen when particle momentum reaches Plank scale! Astrophysical Limits on Lorentz Violation Synchrotron radiation in the Crab Nebula: ce < 6 ×1020 Brett Altschul Spectrum of Ultra-high energy cosmic rays at Auger: c-cp < 6 ×1023 Scully and Stecker Spin limits can do better….! I Search for CPT-even Lorentz violation with nuclear spin Need nuclei with orbital angular momentum and total spin >1/2 Quadrupole energy shift due to angular momentum of the valence nucleon: EQ ~ (c11 c22 2c33 ) p x2 p y2 2 p z2 I,L px2 p y2 2 pz2 0 pn Previously has been searched for in two experiments using 201Hg and 21Ne with sensitivity of about 0.5 Hz Bounds on neutron cn<1027 – already most stringent bound on c coefficient! Suppressed by vEarth I 21Ne-Rb-K co-magnetometer Replace 3He with 21Ne A factor of 10 smaller gyromagnetic ratio of 21Ne gives the co-magnetometer 10 times better energy resolution for anomalous interactions Use hybrid optical pumping KRb21Ne Allows control of optical absorption of pump beam, operation with 10 times higher Rb density, lower 21Ne pressure. Overcomes faster quadrupole spin relaxation of 21Ne Eventually expect a factor of 100 gain in sensitivity over K-3He comagnetometer Overall, the experimental procedure is identical except the signal can be at either 1st or 2nd harmonic of Earth rotation rate I Search for CPT-even Lorentz violation with 21Ne-Rb-K co-magnetometer About 2 month of data collection Just completed preliminary analysis Sensitivity is about a factor of 100 higher than previous experiments Limited by systematic effects due to Earth rotation Tensor frequency shift resolution ~ 4 nHz E-W Earth rotation signal is ~10 times larger in magnetic field units N-S Causes extra drift of N-S signal due to changes in sensitivity I Results of Tensor Lorentz-Violation Search × 10-29 2w 1w East-West North-South Comb. cxxcyy 0.86 ±1.1 ±0.56 3.6 ±2.8 ±1.6 1.2 ±1.1 cxx+cyy 0.14 ±1.1 ±0.56 0.57 ±2.8 ±1.6 0.19 ±1.1 cyz+czy 5.2 ±3.9 ±2.1 4.2 ±15 ±18 4.8 ±4.3 cxz+czx 4.1 ±2.2 ±2.4 17 ±14 ±13 3.5 ±3.2 Constrain 4 out of 5 spatial tensor components of c at 1029 level Improve previous limits by 2 to 3 orders of magnitude Most stringent constrains on CPT-even Lorentz violation! Assume Schmidt nucleon wavefunction – not a good approximation for 21Ne – need a better wavefunction Assume kinetic energy of valence nucleon ~ 5 MeV I Recent compilation of Lorentz limits I 1033 GeV Natural size for CPT-even Lorentz violation ? 1029 GeV m2 c ~h M pl2 m - SUSY breaking scale? h 1 allowed for m =1 TeV V.A. Kostelecky and N. Russell arXiv:0801.0287 v4 Need to get to c ~ 10-3110-32 Systematic errors Most systematic errors are due to two preferred directions in the lab: gravity vector and Earth rotation vector If the two vectors are aligned, rotation about that axis will eliminate most systematic errors Amundsen-Scott South Pole Station Within 100 meters of geographic South Pole No need for sidereal fitting, direct measurement of Lorentz violation on 20 second time scale! I Conclusions Precision atomic physics experiments have been playing an important role in searches for New Physics Currently severely constrain CP violation beyond the Standard Model Place stringent constraints on CPT and Lorentz violation at the Planck scale Important constraints on spin-dependent forces, variation of fundamental constants, other ideas. I