Download ppt - UCSC Bayesian Data Analysis Workshop

Event Analysis for the
Gamma-ray Large Area
Space Telescope
Robin Morris, RIACS
Johann Cohen-Tanugi
INFN, Pisa
Why study gamma-rays?
• Gamma-rays are produced by some of the highest
energy events in the universe, events that are not
yet fully understood.
• Study of these events is critical to understanding
the origins and evolution of the universe.
• The distribution of gamma-rays (both across the
sky and in terms of energy) can confirm theories
about the early universe.
• The Large Area Telescope is designed to map the
incidence of gamma-rays.
• We are developing a Bayesian methodology for
the analysis of the instrument response.
(background - distribution of gamma-rays from EGRET)
The Large Area Telescope (LAT)
• For each incident gamma ray
photon, we want to know its
incident direction and energy
• The LAT has three components:
– Anticoincidence detector eliminates responses due to
incident charged particles
– Array of conversion towers - the
heart of the detector
– Imaging calorimeter - measures the
residual energy in the particles
generated by an incident gamma
ray photon
How the conversion towers work
• Alternating conversion and
detection layers
• Incident gamma rays are
converted into electron/positron
pairs
• The electron and positron
cascade through the detector
– Undergo secondary scattering
– Produce further electrons and
photons
• Each time they cross a detection layer, they trigger the silicon
microstrip detectors, producing a readout
• The output from an event is a set of (x,y,z) positions of the
silicon microstrips that were triggered (+ calorimeter response)
Examples (from the GLEAM simulator)
200MeV photon
• blue line - incident photon and
electron/positron
• orange - microstrip detectors
• blue cubes - calorimeter
• green - anticoincidence detector
points to note:
• inherent ambiguity in the number
of particles at each layer
• significant secondary scattering
• production of secondary electrons
(hits to left of main track)
• anticoincidence detector fired by
secondary electrons
• opening angle depends on energy
GLEAM - GLAST Event Analysis Machine
Examples (from the GLEAM simulator)
100GeV photon
•
•
•
•
•
secondary photons are suppressed
in the figure (to enable the
secondary electron tracks to be
seen)
very small opening angle
huge number of secondary
electrons (black “cloud”)
lots of firing from the secondary
electrons
firings well away from the main
track (from secondary photons
converted into charged particles)
Physics Processes
Pair production
• conversion of gamma ray photons into
electron/positron pairs
multiple coulomb scattering
• charged particles are deflected on interacting
with (primarily) atoms
positron anihilation
• positron + electron => photons
ionisation
• liberation of electrons from atoms by the transfer
of (at least) the binding energy from a particle to
the electron
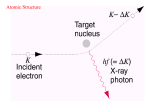
bremsstrahlung
• radiation emitted by a charged particle undergoing acceleration (typically deceleration when
passing through the field of atomic nuclei)
photoelectric effect
• ejection of electrons from the surface of material by incident photons
compton scattering
• transfer of energy from photons to electrons; may liberate bound electrons
Pair Production - energy and angles
photon
E
•
•
fe
electron
Ee
•
fp
positron
Ep
•
•
The tungsten conversion foils are
0.105mm thick, resulting in a
conversion probability of ~2% for
photons of 1GeV
The lowest 4 foils are 0.723mm
thick (~10% conversion probability)
Compromise between pair
production and multiple scattering
and other physics processes that
hide the primary event
The energy of the incident photon is
divided between the electron and
positron
The electron/positron angle
depends stochastically on the
electron/positron energy
Pair Production - energy and angles
•
Distribution of energy split between
electron and positron as a function
of photon energy
•
Distribution of electron/positron
angle
me c 2
f 
u
E
where u is distributed as above

Other electron/positron processes
Currently we include
multiple scattering
ionisation
bremsstrahlung
Using the Geant4 physics
simulation toolkit, we simulate the
interaction of electrons with the
tungsten foils, and estimate the
scattering distributions
Apart from the tails, the distribution
can be approximated by a gamma
distribution
We currently neglect other physics
processes/particles
Simplified Simulation
Using the physics distributions
described so far, we implemented a
simulation of the detector
• uses the LAT geometry
• only includes the primary electron
and positron
• doesn’t include energy deposition
by particles as they pass through
matter
Over-simplified Simulation
• Reduce the detector to 2D
• Keep the physical distributions
–
–
–
–
conversion
energy distribution
opening angle
scattering distributions
- neglect all other
physics processes
Probabilistic event analysis
Incorporate data one layer at a time:
• p(q)
• p(q | d1) ~ p(d1 | q)p(q)
• p(q | d1,d2) ~ p(d2 | q)p(d1 | q)p(q)
• p(q | d1,d2,…dN) ~
p(dN | q)p(dN-1 | q) … p(d2 | q)p(d1 | q)p(q)
Probabilistic event analysis
Incorporate data one layer at a time:
• p(q)
• p(q | d1) ~ p(d1 | q)p(q)
• p(q | d1,d2) ~ p(d2 | q)p(d1 | q)p(q)
• p(q | d1,d2,…dN) ~
p(dN | q)p(dN-1 | q) … p(d2 | q)p(d1 | q)p(q)
Probabilistic event analysis
Likelihood:
•
p(d | q)
•
This is zero-one - if the trajectory described by q
triggers all the detectors that fired, then p(d | q)=1,
else p(d | q)=0
•
This makes applying MCMC directly somewhat
difficult.
•
This is a simplification of the likelihood
–
–
–
some detectors fire spuriously
some particles pass through gaps between microstrips
information regarding the particles energy
Computation
• The basic idea:
– run the forward simulation a very large number of times, keeping
those runs which triggered the same detectors that were triggered
in the event we are analysing
– compute the mean, variance etc of the photon direction and energy
from the runs that are retained
– clearly this is computationally infesable (and becomes more so the
more physics processes we include)
•
Instead:
– use ideas from sequential importance sampling to only generate
runs that with high probability trigger the detectors that fired
– non-parametric representation of the distribution that allows for
tracking of multiple hypotheses
Computation
A combination of ideas from Particle Filters and MCMC
• represent p(q | {d}) by a set of particles
• propagate the set of particles down the stack
– use importance sampling distributions that generate trajectories
that intersect, with high probability, with the detectors that fired
(0-1 likelihood)
– weight the particles by the ratio of the physics distribution to the
importance sampling distribution
– re-sample the set of weighted particles
• apply mcmc steps to the particles after each layer
– because the event has no dynamics between layers (the photon
angle does not change), “particle starvation” can be a problem
Over-simplified simulation
•
•
•
Only analyse the incident photon angle and position
Also estimate the “nuisance” variables - the vertex position (shown) and scattering angles at
each layer (not shown)
Assume the energy split between the electron and positron is known (see later)
Over-simplified simulation
•
•
The energy split is almost equal, so the “opening angle” is symmetric (107:93MeV)
Because the positron (blue) is scattered much less, a good fit to the data is a slightly offset
photon angle, with more even scattering down the two trajectories
Over-simplified simulation
•
•
Very small opening angle, so energy split is less important (actual split is 154:46MeV)
Estimate is unbiased, but the remaining uncertainty is larger
Simplified Simulation
•
Show the results for the estimate of the photon
angles for the first four levels
(after that particle starvation became an issue)
Future work
• Add more physics
– add the analysis of the energy of the photon, and consider also the
deposition of energy by the particles as they interact with the
detector
– addition of the processes which produce secondary particles will
complicate the analysis significantly
• the dimensionality of the particles will vary
•
Improve the likelihood:
– currently we use a simple 1-0 likelihood
– model the physics of the silicon microstrip detectors
• the microstrips give information about the quantity of charge deposited
• the number of strips that fire depends on the energy of the incident
particles
Future work
• Analysis of the energy
– the angle distribution is highly dependent on the energy split between the
electron and positron
photon
200MeV
fe
electron
80MeV
photon
200MeV
fe
fp
positron
120MeV
electron
190MeV
fp
positron
10MeV
Conclusion
“If you have to use statistics, go back and design the
experiment properly”
Lord Rutherford
“If you have to use statistics, think about the statistics at
the same time as you design the experiment”
Me