Download CHAPTER 4: Basic Estimation Techniques

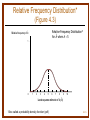
Chapter 4: Basic Estimation
Techniques
McGraw-Hill/Irwin
Copyright © 2011 by the McGraw-Hill Companies, Inc. All rights reserved.
Basic Estimation
• Parameters
• The coefficients in an equation that determine
the exact mathematical relation among the
variables
• Parameter estimation
• The process of finding estimates of the
numerical values of the parameters of an
equation
4-2
Regression Analysis
• Regression analysis
• A statistical technique for estimating the
parameters of an equation and testing for
statistical significance
4-3
Simple Linear Regression
• Simple linear regression model relates
dependent variable Y to one independent
(or explanatory) variable X
Y  a  bX
• Intercept parameter (a) gives value of Y where
regression line crosses Y-axis(value of Y when X is
zero)
• Slope parameter (b) gives the change in Y
associated with a one-unit change in X:
b  Y X
4-4
Random Effect
Firm expects $10,000 in sales from each agency plus an additional
$5 in sales from each additional $1 of advertising.
Si  10,000  5 Ai  ei
4-5
Simple Linear Regression
• Parameter estimates are obtained by
choosing values of a & b that minimize the
sum of squared residuals
• The residual is the difference between the actual
and fitted values of Y: Yi – Ŷi
• The sample regression line is an estimate of
the true regression line
ˆ
Yˆ  aˆ  bX
4-6
Sample Data
•Time series data – values taken by a variable over
time
•Cross sectional data – values for multiple
occurrences of a variable at a point in time
4-7
Sample Regression Line
(Figure 4.2)
S
Population regression line – true regression line
Sample regression line – estimate of the true regression line
SSii = 60,000
60,000
70,000
Sales (dollars)
60,000
ei
50,000
20,000
10,000
•
•
40,000
30,000
•
Sample regression line
Ŝi = 11,573 + 4.9719A
•
46,376
ŜŜ
46,376
i=
i 
•
•
•
A
0
2,000
4,000
6,000
8,000
10,000
Advertising expenditures (dollars)
4-8
The Method of Least Squares
( X i  X )(Yi  Y )
ˆ
b
2
( X i  X )
aˆ  Y  bˆX
4-9
Statistical Output - Excel
Y=11573.0 + 4.97191X
4-10
Three Kinds of Correlation
4-11
Unbiased Estimators
• The estimates â & b̂ do not generally equal
the true values of a & b
• â & b̂ are random variables computed using
data from a random sample
• The distribution of values the estimates
might take is centered around the true
value of the parameter
4-12
Unbiased Estimators
• An estimator is unbiased if its average
value (or expected value) is equal to the
true value of the parameter
4-13
Example of an Unbiased Estimate
You blindly draw 5 balls from a pot containing 80 red balls and 20 blue
balls. What is the probability of drawing a sample that proportionately
replicates the percentage of red and blue balls in the pot? You might draw
all red balls and inaccurately predict that there are no blue balls in the pot.
Now place the balls back in the pot and draw another sample of 5 balls. As
you repeat this exercise and average the percentage of red and blue balls in
your samples, the average should approach the population average.
The average percentages in the samples is an unbiased estimate of the
population average. The greater the number of draws, the closer you will
likely come to accurately predicting the characteristics of the population.
4-14
Statistical Significance
• Must determine if there is sufficient
statistical evidence to indicate that Y is
truly related to X (i.e., b  0)
• Even if b = 0, it is possible that the
sample will produce an estimate b̂ that is
different from zero
• Test for statistical significance using
t-tests or p-values
4-15
Relative Frequency Distribution*
(Figure 4.3)
Relative Frequency Distribution*
for bˆ when b  5
ˆ
Relative frequency of b
1
0
1
2
3
4
5
6
7
8
9
10
ˆ
Least-squares estimate of b (b)
*Also called a probability density function (pdf)
4-16
Errors Around Regression Line
f(e)
Y
X1
X2
X
4-17
Statistical Significance
• Confidence interval
• An estimate of a population parameter that
consists of a range of values bounded by
statistics called upper and lower confidence
limits, within which the value of the parameter
is expected to be located.
• Probability Density Function (PDF)
• The statistical function that shows how the
density of possible observations in a
population is distributed.
 Areas under the PDF measure probabilities
4-18
Relative Frequency Distribution*
(Figure 4.3)
ˆ
Relative frequency of b
Relative frequency of estimated
b when true b is zero
1
Estimated
b
Probability of Type I
error- finding parameter
significant when it is not
True b
-5
-4
-3
-2
-1
0
1
2
3
4
5
ˆ
Least-squares estimate of b (b)
*Also called a probability density function (pdf)
4-19
Test for Statistical Significance
• To test for statistical significance we need a
statistic for measuring deviations from the
mean value
• The standard error of the estimate provides
that measure
• t-value measures how many standard errors
we are from the mean
bˆ
t
Sbˆ
• The t-test indicates whether the slope
parameter is statistically significant
4-20
Statistical Significance
4-21
Statistical Output - Excel
Y=11573.0 + 4.97191X
4-22
Performing a t-Test
• First determine the level of significance
• Probability of finding a parameter estimate to
be statistically different from zero when, in
fact, it is zero
• Probability of a Type I Error
• 1 minus level of significance = level of
confidence
4-23
Performing a t-Test
• t-ratio is computed as
b̂
t
Sb̂
where Sb̂ is the standard error of the estimate bˆ
• Use t-table to choose critical t-value with
n – k degrees of freedom for the chosen
level of significance
•
n = number of observations
• k = number of parameters estimated
4-24
Student t Distributions
The fewer the degrees of freedom, the flatter is the distribution.
4-25
Degrees of Freedom
• Number of observations you have less the
minimum number of observations needed
to fit the curve
• 2 observations are needed to fit a straight
line
• 3 observations are needed to fit a plane in
3-D space
4-26
Performing a t-Test
• If the absolute value of t-ratio is greater
than the critical t, the parameter estimate
is statistically significant at the given level
of significance
4-27
df = n – k
n=7
k=2
df = 5
4-28
Statistical Output - Excel
Y=11573.0 + 4.97191X
t* = 2.571
4-29
Using p-Values
• Treat as statistically significant only those
parameter estimates with p-values smaller
than the maximum acceptable significance
level
• p-value gives exact level of significance
• Also the probability of finding significance
when none exists
4-30
Statistical Output - Excel
Y=11573.0 + 4.97191X
t* = 2.571
4-31
Coefficient of Determination
• R2 measures the percentage of total
variation in the dependent variable (Y) that
is explained by the regression equation
• Ranges from 0 to 1
• High R2 indicates Y and X are highly
correlated
4-32
High and Low Correlation
4-33
Coefficient of Determination (R2)
Y
SSE (unexplained)
SST
SSR (explained)
_
Y
X
R2 – ratio of explained to total variation
4-34
Statistical Output - Excel
Y=11573.0 + 4.97191X
t* = 2.571
4-35
F-Test
• Used to test for significance of overall
regression equation
• Measures goodness of fit
• F value (ratio of explained to unexplained
sum of squares)
• Compare F-statistic to critical F-value from Ftable
• Two degrees of freedom, k – 1 & n – k
• Level of significance
• If F-statistic exceeds the critical F, the
regression equation overall is statistically
significant
4-36
Example:
n-k = 5
k-1 = 1
4-37
Statistical Output - Excel
4-38
F-Test
• If F-statistic exceeds the critical F, the
regression equation overall is statistically
significant at the specified level of
significance
4-39
4-40
Multiple Regression
• Uses more than one explanatory variable
• Coefficient for each explanatory variable
measures the change in the dependent
variable associated with a one-unit change
in that explanatory variable, all else
constant
4-41
Quadratic Regression Models
• Use when curve fitting scatter plot is
shaped or ∩-shaped
• Y = a + bX + cX2
U-
• For linear transformation compute new variable
Z = X2
• Estimate Y = a + bX + cZ
• ΔY/ΔX = b + 2cX
• At min or max X= -b/2c
• c is positive (negative) if there is a
minimum (maximum)
4-42
Quadratic Regression
4-43
4-44
Log-Linear Regression Models
• Use when relation takes the form: Y = aXbZc
Percentage change in Y
•b=
Percentage change in X
Percentage change in Y
•c=
Percentage change in Z
• Transform by taking natural logarithms:
lnY  lna  bln X  c ln Z
• b and c are elasticities
4-45
Log Linear Regression
4-46
4-47