* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Modeling Cytomegalovirus Infection
Urinary tract infection wikipedia , lookup
Adaptive immune system wikipedia , lookup
Sociality and disease transmission wikipedia , lookup
Psychoneuroimmunology wikipedia , lookup
Cancer immunotherapy wikipedia , lookup
Hygiene hypothesis wikipedia , lookup
Cryptosporidiosis wikipedia , lookup
Adoptive cell transfer wikipedia , lookup
Innate immune system wikipedia , lookup
Immunosuppressive drug wikipedia , lookup
Infection control wikipedia , lookup
Hepatitis B wikipedia , lookup
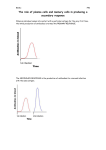
A Mathematical Model of Cytomegalovirus (CMV) Infection in Transplant Patients Grace M. Kepler Center for Research in Scientific Computation North Carolina State University Outline • • • • • • Significance Modeling goals Mathematical/Biological model Parameter approximation Numerical results Conclusions Transplantation Numbers (UNOS, 2005) The number of individuals waiting for, receiving, or living with a transplanted organ(s) is significant. • More than 27,000 organs transplanted • Approximately 90,000 waiting for organs • 153,000 living with functioning organ transplant Life-long immunosuppression is the standard of care for transplant patients. Immunocompromised individuals are susceptible to infections from • Common pathogens (eg., influenza) • Opportunistic infections (eg., Listeria) • Latent infections (eg., HCV, VZV, CMV) CMV infection • Most significant threat to patient and graft health • Directly or indirectly causes: – allograft rejection – decreased graft and patient survival – predisposition to opportunistic infections and malignancies Facts about CMV • A herpes virus • 50-90% of adults are infected (geographic variation) • Primary infection in immunocompetent individuals is generally asymptomatic (some get mononucleosis-like illness ) • Establishes lifelong latent infection • Latent infection is well control by healthy immune systems • Reactivation rare in healthy individuals CMV Infection Risk In Transplantation Donor Recipient Type D+ R- primary D- R+ reactivation D+ R+ superinfection D- R- risk with exposure Optimal care of individuals with transplanted organs is important • No universal agreement among transplant centers about – Prophylactic vs. preemptive antiviral treatment – Optimal duration of antiviral treatment • Optimal treament may vary among subpopulations (eg., D+ R- vs D- R+) Modeling goals • Create a within-patient dynamic model of CMV infection • Describe dynamics of cell and viral populations with ODEs x(t ) f ( x, t; ) Model parameters Modeling goals • Individualized medicine – model equations are the same for each individual – model parameter values may vary among individuals – individuals are characterized by their particular set of parameter values – parameter values for each individual determine their particular infection dynamics – allowing prediction for each individual Longitudinal data Viral load data for one individual. Censored data Parameter estimation Estimate model parameters from the data. Prediction Use the model and characterstic parameters to predict infection dynamics. Modeling goal – Population predictions • Estimate characteristic parameters for many individuals using longitudinal data Modeling goal – Population predictions • Create a probabilistic model to describe parameter distributions Modeling goal – Population predictions • Use the probabilistic model to create virtual patients • Predict population behavior (eg., treatment regimens) Antiviral treatment Modeling goal – Population predictions • Use a stochastic model to sample the parameter distributions (virtual patients) • Predict population behavior (eg., treatment regimens) Antiviral treatment Modeling goal – Population predictions • Use a stochastic model to sample the parameter distributions (virtual patients) • Predict population behavior (eg., treatment regimens) Antiviral treatment Modeling considerations • Start simply, capture most salient biological features – a model that can describe primary, latent, and reactivated infections in healthy or immunocompromised individuals • Use clinical measurements to inform the model • Model cell and viral populations in the blood Math/Bio model - virions VIRIONS (free virus) Math/Bio model – susceptible cells SUSCEPTIBLE CELLS (monocytes) cell replication and death Math/Bio model actively-infected cells ACTIVELY INFECTED CELLS Math/Bio model – viral-induce cell lysis Math/Bio model – immune response CMV-SPECIFIC IMMUNE EFFECTOR CELLS Math/Bio model – immune suppression Math/Bio model – lysing of infected cells Math/Bio model – latently-infected cells LATENTLYINFECTED CELLS Math/Bio model – reactivation reactivation of monocytes upon differentiation Math/Bio model – cell replication/death State Variables Variable Description Units V virions virions/mL-blood E cells/mL-blood RI virus-specific immune effector cells actively-infected cells RS susceptible cells cells/mL-blood RL latently-infected cells cells/mL-blood cells/mL-blood Mathematical equations V n RI cV fkRSV E E (1 òS ) E 1 E V e RI kRSV RI (1 òS )mERI 0 RL RI RS RS 1 rS RS kRSV RL RL 1 rL RL 0 RL RI Clinical data Longitudinal measurements • Real-time quantitave PCR measurements of viral DNA in plasma ( V ) • Antigenemia assay ( RI ) • PBMC depleted ELISPOT assay ( E ) Statistical framework • Intra-subject variation of observations – assay errors – physiological fluctuations – assay limits (cesored data) Parameter approximations • Physiological information • Experimental measurements , 0 , rS , rL • Auxilliary parameters Viral load decay tH , tD , E,V • Using reduced models for specific time regimes k , c, m, E Unknown parameters Emery1999 , n, e, , Parameter approximations • Provide initial values for parameter estimation when data is available • Allow exploratory simulations of model behavior Immunocompetent ( s 0) Primary infection 4 2 Initial conditions: (V , E , RI , RS , RL ) (110 , 0, 0, 4 10 , 0) Immunocompetent ( s 0) Latent infection V E RI • The latent infection state is characterized by the equilibrium levels of the state variables following primary infection. (V , E, RI , RS , RL ) Immunosuppression Primary infection s 0 Immunosuppression Primary infection s 0.4 Immunosuppression Primary infection s 0.7 Immunosuppression - Latency D-R+ Transplant Scenario • The donor tissue has no CMV virions or latently-infected cells (D-) • Prior to transplantation, recipient has a latent CMV infection, characterized by low levels of V, RI, and RL that is controlled by the immune effector cells E • After transplantation, pharmacolgical immunosuppression can result in a secondary (reactivated) CMV infection Reactivation Immune suppression of an individual with a latent CMV infection V s 0.7 E RI Conclusion • Created a mathematical model for CMV infection in both immunocompetent and immunocompromised individuals • Identified data that can be collected to inform the model • Approximated values for most of the model parameters • Model exhibits primary, latent, and secondary (reactivated) infections • Latent infection is characterized by low-level viral load and actively-infected cells • Simulation of reactivated infection approximates CMV infection in D-R+ transplant patients CMV infection in other immunocompromised individuals • Most common congenital infection – can result in developmental and sensory disabilites • Retinitis infection in AIDS patients. • CMV CTL-inflation may be a cause of immunosuppression in elderly individuals Challenges • Get data – parameter estimation – predictive capability • Further model development – other transplant situations (eg., D+R-) – HLA type, antiviral treatment,... Collaborators • Tom Banks, CRSC, NCSU • Marie Davidian, CQSB, NCSU • Eric Rosenberg, MGH, Harvard