Download constant pressure

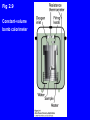
Peter Atkins • Julio de Paula
Atkins’ Physical Chemistry
Eighth Edition
Chapter 2
The First Law
Copyright © 2006 by Peter Atkins and Julio de Paula
Heat transactions
In general: dU = dq + dwexp + dwe
where dwe ≡ extra work in addition to expansion
At ΔV = 0 and no additional work:
dU = dqV
For a measurable change:
ΔU = qV
• Implies that ΔU can be obtained from measurement of heat
• Bomb calorimeter used to determine qV and, hence, ΔU
Fig 2.9
Constant-volume
bomb calorimeter
Fig 2.10 Change in internal energy as function of temperature
The heat capacity
at
constant volume:
 U 
CV  

 T  V
Slope = (∂U/∂T)V
Fig 2.11
Change in internal energy
as a function of temperature
and volume
• U(T,V), so we hold one
variable (V) constant,
and take the ‘partial
derivative’ with respect
to the other (T).
 δU 
CV  

 δT  V
Fig 2.12
At constant volume: dU = dq
If system can change volume,
dU ≠ dq
• Some heat into the system
is converted to work
• ∴ dU < dq
• Constant pressure processes
much more common than
constant volume processes
If CV is assumed to be constant with temperature for
macroscopic changes:
ΔU = CV ΔT
qV = CV ΔT
or:
Enthalpy ≡ heat flow under constant pressure
H ≡ U + PV
ΔH = ΔU + PΔV
ΔH = ΔU + ΔngRT
Fig 2.14
Plot of enthalpy as a
function of temperature
The heat capacity
at
constant pressure:
CP = (∂H/∂T)P
 H 
CP  

 T  P
Cp > Cv
Cp – Cv = nR
CV = (∂U/∂T)V
Variation of enthalpy with temperature
 H 
CP  

 T  P
If CP is assumed to be constant with temperature for
macroscopic changes:
ΔH = CP ΔT
qP = CP ΔT
or:
If ΔT ≥ 50 oC, use empirical expression, e.g.:
CP,m  a  bT 
c
T2
with empirical parameters from
Table 2.2
Adiabatic Changes
• Consider change of state:
Ti, Vi → Tf, Vf
• Internal energy is a
state function
∴ change can be
considered in two steps
Fig 2.17
Variation of temperature
as a perfect gas is
expanded reversibly
and adiabatically:
Vf Tfc  ViTic
where:
c 
CV ,m
R
Fig 2.17
Fig 2.18 (a) Variation of
pressure with volume in a
reversible adiabatic expansion
Pf Vfγ  Pi Viγ
where the heat capacity ratio:
γ
CP,m
C V ,m
Fig 2.18 (b)
• Pressure declines more
steeply for an adiabat
than for an isotherm
• Temperature decreases
in an adiabatic expansion