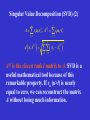Download University of Florida - University of Missouri

ARMY RESEARCH OFFICE
Military University Research Initiative
Oct 16, 2003
Rodney J. Bartlett
Co-Workers
Dr. Marshall Cory
Dr. Stefan Fau
Mr. Josh McClellan
Quantum Theory Project
Departments of Chemistry and Physics
University of Florida
Gainesville, Florida USA
OUTLINE
I. INTRODUCTION
Nature of problem and our objectives
II. NUMERICAL RESULTS
Dimethylnitramine and tests of quantum chemical methods to be
used. (Stefan Fau)
III. PLAN AND PROGRESS FOR RDX
(Stefan Fau, Marshall Cory)
IV. COMPRESSED COUPLED CLUSTER THEORY: A NEW
APPROACH TO HIGH LEVEL CC FOR LARGE MOLECULES
V. SUMMARY OF PROGRESS AND FUTURE PLANS
University of Florida: Quantum Theory Project
OBJECTIVES
Identify and characterize the initial steps in nitramine detonation in the condensed phase.
Study the series of molecules, nitramine (gas phase), methyl nitramine(liquid),
dimethylnitramine(solid) which have
(1) different reaction paths
(2) different condensed phase effects
Investigate their unimolecular, secondary, and bimolecular reaction mechanisms.
Obtain definitive results for the comparative activation barriers for different unimolecular paths
including those for RDX.
Develop ‘response/dielectric function’ methods to incorporate the condensed phase effects into
the quantum mechanical calculations.
Provide high-level QM results to facilitate the development of classical PES for large scale
simulations.
Generate ‘transfer Hamiltonians’ to enable the direct dynamics simulations as a QM complement
to classical potentials.
University of Florida: Quantum Theory Project
Quantum Mechanics I (Isolated gas phase molecules, 0K)
Potential Energy Surface E(R)
Different Unimolecular Decomposition Paths
Activation Barriers
Spectroscopic signatures for intermediates and products
Quantum Mechanics II
Bi(tri...)molecular reactions
Long range (condensed phase, pressure) effects
Activation Barriers, Spectroscopy
Classical Mechanics-Representation E(R)
Large Molecule QM-Simplified Representation
of H(R) Transfer Hamiltonian
Electronic State Specific
SEAMLESS WHOLE…
FROM QM [(CC) TO (DFT)TO (TH)]
TO ADAPTIVE (CHARGE TRANSFER) POTENTIALS,
TO CLASSICAL POTENTIALS (CP),
AND BACK, ie
INSIST THAT E(R)
LEADS BACK TO A H(R), THAT GIVES
ELECTRONIC DENSITY AND OTHER
QM PROPERTIES
Reactions of one H2N-NO2
H2N-NO2  H2N. + NO2.
 H + HN -NO2
.
.
 H2N-ONO
[ HN=N(O)OH]  3HN + 1HONO
( 1HN + 1HONO)
( 3HN + 3HONO)
Reactions of two H2N-NO2
Same reactions as before, causing a slight change in the
interaction energy with the second H2N-NO2.
Additionally:
H2N-NO2 + H2N-NO2  H2N-NH2 + NO2. + NO2.
 NH2. + NH2. + O2N-NO2
 H2NH + NO2. + HN.-NO2
 H2N. + HONO + HN.-NO2
Reactions of one Me2N-NO2
Me2N-NO2  Me2N. + NO2.
 MeN -NO2 + Me
.
.
 H2C.-N(Me)-NO2 + H.
[ H2C=N+(Me)-N(O-)OH]  H2C=NMe + HONO
Reactions of two Me2N-NO2
Same reactions as before, causing a slight change in the
interaction energy with the second Me2N-NO2.
Additionally:
Me2N-NO2 + Me2N-NO2  Me2N-ONO + Me2N. + NO2.
 Me2N-NMe2 + NO2. + NO2.
 Me2N-Me + Me-N.-NO2 + NO2.
 Me2N-N(Me)-NO2 + Me. + NO2.
 Me2N-H + H2C.-N(Me)-NO2 + NO2.
 Me2N-CH2-N(Me)-NO2 + H. + NO2.
products from CH3., H. (HONO, H-Me, …)
Dimethylnitramine
Overview
• Immediate goals and methods
• Dimethylnitramine
• RDX
• Other Things We Can Do
Goals of Our Calculations
 Provide high quality energies (forces where feasible)
at points along various reaction coordinates for testing
or fitting of faster methods.
 Definitive answers for low energy dissociation
reactions of dimethylnitramine (and more reliable ones
for RDX).
 Use nitramine as a test-case since better methods can
be used. (More complete work if desired.)
 Environmental effects by including second molecules.
How we do it
DFT:
 generally good minimum geometries
 less good for transition states, vdW, ...
 cheap
CCSD(T):  good energies (and other properties)
 expensive.
Basis set extrapolation:
 necessary for high quality energies, ...
 Single-point energies with basis set extrapolation
on DFT/TZ minima and reaction paths.
Basis Set Extrapolations
 X1
CBS3:
EXZ  EZ  Ae
CBS2:
E XZ  E Z  Ae  X1
 E Z
  X12
 Be
e 1
ETZ  EDZ 
 EDZ  1
2
e e
Let’s introduce empirical parameters ...
CBSxf: EZ  EDZ  aECBSx  EDZ 
CBSxM:
DECBSx-DZ from MBPT(2)
(PWD)
A Broader Test of Basis Set
Extrapolation Schemes
(H3C)2N-NO2,
H2C=N-CH3, cis HONO, 2A1 NO2, 2A2" CH3, H,
H2C=NH, HCN, NH3, 2B2 NH2, 3Sg NH,
HNO, 2P NO, N2O,
3B CH , H CO, CO, CO ,
2
2
2
2
H2O, 2P HO
CBS3(MP2)
CBS3(CCSD)
CBS3(CCSD(T))
CBS3M
-12
std. dev.
CBS2M
avg.
CBS2(CCSD(T))
H2C=NMe
CBS2(CCSD)
H2C=NH
CBS2(MP2)
HN, 3sigma(g,-)
H2CO
HCN
CO2
CO
H2O
OH, 2P
CH3, 2A2"
CH2, 3B2
HNO
N2O
NO(.)
NH3
H2N(.), 2B2
cis HONO
H(.)
NO2(.), 2A1
Me2N-NO2
calc. - exp. [kcal/mol]
Error of calculated gas-phase D fH
riBP86/TZVP
12
9
6
3
0
-3
-6
-9
std. dev.
avg.
H2CO
HCN
CBS3(CCSD(T))
CO2
CO
H2O
OH, 2P
CH3, 2A2"
CBS2(CCSD(T))
CH2, 3B2
HNO
N2O
NO(.)
CBS2M
NH3
H2N(.), 2B2
cis HONO
H(.)
NO2(.), 2A1
Me2N-NO2
calc. - exp. [kcal/mol]
Error of calculated gas-phase D fH
CBS2Mf + add. corr.
3
2
1
0
-1
-2
-3
Definition of CBS2Mf+
E(CBS2Mf) = E(CCSD(T)-fc/cc-pVDZ)
+ 0.81 * DEMBPT(2)-fc(CBS2 - cc-pVDZ)
For enthalpies of formation (riBP86/TZVP freqs.):
H(CBS2Mf+) = H(CBS2Mf) + 0.16 + S nR * cR
c(H2)
c(CH4)
c(N2)
c(O2)
= -0.24
= -0.31
= -0.17
= -1.81
Determined by minimizing RMS of DfHc-DfHe.
Average error: 0.00 Standard deviation: 0.75 kcal/mol
Properties of the Extrapolation Scheme
• Standard deviation 0.75 kcal/mol.
• Using small reference molecules saves more
expensive calculations.
• T2 diagnostic allows judgement of reliability for every
molecule! (Max. T2 < 0.15 is good. Calculations with
larger T2 may be unreliable.)
• Anions need diffuse basis sets in the gas-phase.
A Difficult Reaction Path
H2N-NO2 -> H2N. + NO2. singlet & triplet
120
100
Erel [kcal/mol]
80
t-MBPT(2)-fc/DZ
t-CCSD-fc/DZ
t-CCSD(T)-fc/DZ
t-MBPT(2)-fc/CBS2(XZ)
t-CCSD-fc/CBS2(XZ)
t-CCSD(T)-fc/CBS2(XZ)
100 * max. T2 (t)
60
40
20
0
1
2
3
4
rNN
5
6
7
A Difficult Reaction Path
H2N-NO2 -> H2N. + NO2. singlet & triplet
120
MBPT(2)-fc/DZ
CCSD-fc/DZ
CCSD(T)-fc/DZ
CCSDT-1a-fc/DZ
MBPT(2)-fc/CBS2(XZ)
CCSD-fc/CBS2(XZ)
CCSD(T)-fc/CBS2(XZ)
100 * max. T2 (s)
t-MBPT(2)-fc/DZ
t-CCSD-fc/DZ
t-CCSD(T)-fc/DZ
t-MBPT(2)-fc/CBS2(XZ)
t-CCSD-fc/CBS2(XZ)
t-CCSD(T)-fc/CBS2(XZ)
100 * max. T2 (t)
100
Erel [kcal/mol]
80
60
40
20
0
1
2
3
4
rNN
5

6
7
H3C-N.-NO2 -> H2C=NH + NO2.
50
40
Erel [kcal/mol]
30
MBPT(2)/CBS2
CCSD(T)/CBS2
CBS2M
MBPT(2)/CBS2f
CCSD(T)/CBS2f
CBS2Mf
BP86/TZVP
CCSD(T)/DZ
100 * max. T2
20
10
N-N bond breaks 
0
-10
-20
rNN=
-30
-1.2
-0.8
-0.4
0.0
rCH - rNH
0.4
0.8
1.2
H2C.-NH-CH3 -> H2C=NH + CH3.
40
Erel [kcal/mol]
30
MBPT(2)/CBS2
CCSD(T)/CBS2
CBS2M
MBPT(2)/CBS2f
CCSD(T)/CBS2f
CBS2Mf
BP86/TZVP
CCSD(T)/DZ
100 * max. T2
20
10
0
1.0
1.5
2.0
2.5
rCN
3.0
3.5
riBP86/TZVP Energies of Some
Primary Reaction Pathways in kcal/mol
(H3C)2N-NO2 
DrE
DFT
DaE
(H3C)2N· + NO2·
46
~49
43.
49
83
=
79
84
H2C·-N(CH3)-NO2 + H·
96
=
90
97
H2C=N-CH3···HONO
-1
~51
-3
-7
H3C-N=NO2CH3
13
~51
12
11
(45)
=
-
·
H3C-N-NO2 + CH3
·
H2C=N(CH3)-NO2H (w. H2O)
CBS2M
DrH
DrH
DFT Energies of Secondary Reactions
[kcal/mol]
DrE
DaE
DrH
DaE w.r.t.
DMNA
(H3C)2N  3P H3C-N + CH3
74.7
=
69.7
121
(H3C)2N  H2C-NH-CH3
-2.9
~39
-2.2
85
H2C-NH-CH3  H2C=NH + CH3
25.1
~29
20.7
72 (85)
H3C -N-NO2  H2C-NH-NO2
-7.2
~39
?
122
H2C-NH-NO2  H2C=NH + NO2
-7.9
~4
?
80 (122)
{H3C -N-NO2  H2C=NH + NO2
-15.1
~39
-17.4}
122
H2C-NCH3-NO2  H2C=NCH3 + NO2
-9.1
~3
-11.4
99
H2C-NCH3-NO2  H2C=NNO2 + CH3
33.1
~38
28.8
134
A Small Summary
 The CBS2Mf+ extrapolation scheme gives enthalpies
of formation with an RMS error of 0.75 kcal/mol.
 The T2 diagnostic indicates reliability of results.
 While riBP86/TZVP is usually within 5-10 kcal/mol
of the CBS2Mf results, the shape of the curves may be
quite different.
 Many reactions have been calculated at the CBS2Mf
level, but this work is not yet complete.
Other Things We Can Do
 Calculate triplet states (possibly important for strongly
deformed geometries).
 Use excited state methods (not quite fire and forget).
RDX
— Gas Phase Dynamics of RDX —
(unimolecular thermal decomposition)
• Purpose: Investigate/Reproduce the findings of Lee et-al1
with respect to the primary event
• Methodology: CCG2MP2/SCFFAF2 (and SCFSCF)
1) Zhao, Hintsa, Lee; JCP 88 801 (1988)
2) Runge, Cory, Bartlett; JCP 114 5141 (2001)
Primary Event1
0.67
3 (H2C-N-NO2) - concerted
RDX
0.33
C3H6N5O4 + NO2 - simple bond rupture
1) Zhao, Hintsa, Lee; JCP 88 801 (1988)
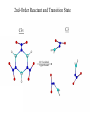
2nd-Order Reactant and Transition State
C3
C3v
62.5 kcal/mol
Upper bound
Current
• Concerted - CCG2MP2 kinetic barrier and reaction swath
information generation
• SBR - Reactant and TS structure optimizations
Future
• Determine the theoretical reaction rates, k(T), and branching
ratios of the primary event
• The future direction of the dynamics work depends on what we
learn from the current effort
Compressed
Coupled Cluster
Singular Value Decomposition
Approach to
Coupled Cluster Calculations
Osamu Hino1, Tomoko Kinoshita2
and Rodney J. Bartlett1
Quantum Theory Project
University of Florida1
Graduate University for Advanced Studies
and Institute for Molecular Science, Japan2
Background
Application of the coupled cluster method to larger
systems → several bottlenecks (CPU, Memory, Disk)
Integral direct algorithm
Parallelization of programs
Local Correlation method
Important to exploit another approach
Use of Singular Value Decomposition
Compressed CC method
Singular Value Decomposition (SVD)
(1)
A  m × n matrix,  m  n 
A  USV T ,
U  m  m orthogonal matrix, u k 
S  m  m diagonal matrix,  s1  s2 
V T  m  n row orthogonal matrix, vTk 
 sm  0 
singular values
left singular vectors
right singular vectors
Singular Value Decomposition (SVD) (2)
m
l
A   sk u k v , A   sk u k vTk
k 1

l 
T
k
l 
d A, A
k 1
    A
m
n
i 1 j 1
ij
l 
 Aij

2
A(l) is the closest rank l matrix to A. SVD is a
useful mathematical tool because of this
remarkable property. If su (u>l) is nearly
equal to zero, we can reconstruct the matrix
A without losing much information.
Application of SVD to the Coupled
Cluster Doubles (CCD) Amplitude (1)
First, we choose an approximate CCD amplitude.
The simplest one is MBPT(2) amplitude. We
assume the Hartree-Fock reference.
 CCD 
ab
ij
t

1
ab
ij
t
SVD
1
W
ab
ij
t
  s pU V ,W  O
p 1
ij
p
ab
p
2
The singular values which are less than the threshold
are neglected.
Application of SVD to the Coupled
Cluster Doubles (CCD) Amplitude (2)
We can define the following contracted two-electron
creation and annihilation operators according to the
SVD of the approximate amplitude.
C  V a a , AI  U a j ai
†
A
ab
A
† †
a b
ij
I
ab
ij
Then we can define the approximate cluster operator.
W
W
1
A †
T2   t I C A AI
2 A I
Physical meaning of the procedures (1)
MBPT(2):  exact   HF  
1 1 ab † †
   tij aa ab a j ai  HF
2 abij
1 1 ab † †
  tij  aa ab vac    a j ai  HF
2 abij

1
†
  sP CP AP  HF
2 P
Reduced density matrix for 
ij ,kl   t
1
ab
 ,cd   t
t , ab
ab 1 ab
ij
kl
1
ij
ab 1 cd
ij
ij
t
Application of SVD to the Coupled
Cluster Doubles (CCD) Amplitude (3)
The CCD equation becomes,
E   HF He  HF
T2
c
,  He  HF
A
I
Degrees of freedom of the equation
 0.
T2
W2
V 2O 2
c
2
O

V2
Most expensive term in CCD calculation

cd
ab cd tijcd   A C t BC , A C 
ab cd
C
V 4, A C
ab
cd
V
ab
cd
V
 A
C
abcd
O4
Integral transformation is required only once.
Improvement of the quality of calculated results
Use better approximate amplitude (e.g. MBPT(3)…).
d

 CCD 
ab
ij
 2
ab
ij
t , t
d
 CCD 
ab
ij
1
t , t
Tighten the threshold.
W
W
1
A †
T2   t I C A AI 
2 A I
W W
1
A †
T2   t I C A AI ,W   W
2 A I
ab
ij

Background
・The CCSD model is one of the most reliable quantum
chemical methods. However, it is often necessary to
incorporate higher order cluster operators than
connected doubles to achieve the chemical accuracy.
・ CCSDT, CCSDTQ, and CCSDTQP are implemented
and they produce highly accurate computational results.
But they are too expensive to be performed routinely.
・ Perturbative approach such as the CCSD(T) or
CCSD(TQ) is one possible solution for this problem. But
still there is a problem that the perturbative approaches
are stable only in the vicinity of equilibrium molecular
geometry.
Purpose of this study
To develop theoretical framework
(1) including the connected triples
(2) accurate
(3) less expensive
(4) stable under deformed molecular geometry
Compression of the connected triples
(1) Apply SVD to the second order triples
 2
OV
abc
ijk
t
  sX Q R
ai
X
X 1
bjck
X
(2) Create contracted mono-excitation operators
C X   QXai a †i, X  1, 2,
,K
ai
(3) Truncate the mono-excitation operator manifold
K   O V ,  1
3
2
2
Easy to manipulate T3 amplitude
(4) Compressed T3 cluster operator
1
T3   t XYZ C X CY CZ
6 XYZ
Compressed CCSDT method
(1) Equations
E   HF H eT1 T2 T3  HF
0 
ab
ij
T1  T2  T3
He
 HF
c
, 0   ia H eT1 T2 T3  HF
T1  T2  T3
c
, 0   XYZ H e
 HF
 XYZ  C X CY CZ  HF
(2) Equations for connected triples
Dijkabc tijkabc  Rijkabc
  DXX  t X YZ   DYY  t XY Z   DZZ  t XYZ   RXYZ ,
X
X
DXX    Dia QXai QXai
ai
X
c
c
Compressed CCSDT-1 method
Approximate treatment for the T3 amplitude
0   ijab H eT1T2 T3  HF
c


 0   XYZ H eT1T2  T3  HF
c
 CCSDT-1a
no approximation for the T2 amplitude
 CCSDT-1b
0   XYZ H eT1T2 T3  HF
c
 0   XYZ H 1  T2   HF
c
・Easiest to implement
・Operation count for T3 amplitude scales as K2V2O
・Iterative counterparts of CCSD[T] and CCSD(T)
Potenrial Energy Curve (1)
(HF, aug-cc-pVDZ, HF-bond stretcing)
0
(E+100)*1000 (a.u.)
-50
-100
r(eq)=1.733 bohr
=0.25
-150
MRCI
CCSD
CCSD(T)
CCSDT-1
COMP.SDT-1
-200
-250
-300
0.5
1
1.5
2
2.5
r(HF)/r(eq)
3
3.5
4
Potential Energy Curve (2)
(H2O, aug-cc-pVDZ, OH-bonds stretching)
(E+76)*1000 (a.u.)
100
0
r(eq)=1.809 bohr
=0.25
-100
MRCI
CCSD
CCSD(T)
COMP.SDT-1
CCSDT-1
-200
-300
0.5
1
1.5
2
2.5
r(OH)/r(eq)
3
3.5
SUMMARY OF PROGRESS
• Detailed study of nitramines to establish the
accuracy of various quantum-mechanical results
for application to uni- and bi-molecular reactions.
• Initial investigation of comparative reaction paths
for DMNA with the goal of providing definitive
results.
• Application to RDX to help resolve the nature of
the initial step in its decomposition.
• Introduced compressed coupled-cluster theory as a
new tool that can provide CC quality results at a
fraction of the current cost.
PLANS FOR 2003-2004
• Resolve issue of comparative energetics
.
among HONO elimination, loss of NO2,
and NO2  ONO in prototypical
nitramines.
• Complete work on primary decomposition
of dimethylnitramine and reactions of
decomposition products with each other and
new dimethylnitramine.
 Apply the methods used with dimethylnitramine to
RDX and compare to relative reaction rates from
established technology.
 Extend the compressed CC method to full triples
and factorized quadruples.
 Formulate analytical gradients for compressed CC.
Backup Slides
Enthalpies of formation for
H2N-NO2 et al. (gas-phase)
-
cis HONO, NO2 (2A1), HN-NO2 , NH3, H2N (2B2),
3
HN ( Sg )
average error [kcal/mol]
B3L/6 CBS2M CBS2 CBS3 G2 CBS-Q
all
0.7
0.0
-0.4 -0.7 -2.2 -1.1
no HN, HN-NO20.0 -0.2
-0.5 -0.6 -1.7 -0.6
Standard deviation for gas-phase D fH
9
8
7
B3LYP/6-31G**
CCSD(T)-fc/DZ
CBS2M
CBS2(CCSD(T))
CBS3M
CBS3(CCSD(T))
G2
CBS-Q
[kcal/mol]
6
5
4
3
2
1
0
all
no HN
no H2N-NO2-
neither
H2N-NO2 -> H2N. + NO2. BS dependence
100
MBPT(2)-fc/DZ
CCSD-fc/DZ
CCSD(T)-fc/DZ
MBPT(2)-fc/CBS2(XZ)
CCSD-fc/CBS2(XZ)
CCSD(T)-fc/CBS2(XZ)
100 * max. T2 (s)
MBPT(2)-fc/ADZ
CCSD-fc/ADZ
CCSD(T)-fc/ADZ
MBPT(2)-fc/CBS2(AXZ)
CCSD-fc/CBS2(AXZ)
CCSD(T)-fc/CBS2(AXZ)
100 * max. T2 (s)
Erel [kcal/mol]
80
60
40
20
0
1
2
3
4
rNN
5
6
7
(H3C)2N-NO2 -> (H3C)2N. + NO2., Cs
70
60
Erel [kcal/mol]
50
MBPT(2)/CBS2
CCSD(T)/CBS2
CBS2M
MBPT(2)/CBS2f
CCSD(T)/CBS2f
CBS2Mf
riBP86/TZVP
CCSD(T)/DZ
100 * max. T2
40
30
20
10
0
1.0
1.5
2.0
2.5
rNN
3.0
3.5
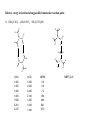
Relative energy in kcal/mol along possible bimolecular reaction paths
.
.
C) 2 Me2N-NO2  MeN-NO2 + Me2N-NO2Me
H
H
H
H
O
H
-
+
N
H
N
O
H
N
H
O
H H
C
H
-
H
H
O
+
N
H
+
N
N
O
+
O
H
O
N
H
H
O
H H
-
H
N
H
H
-
H
H
r(CN)
1.460
1.462
1.468
1.485
1.568
2.281
3.247
r(CO)
3.450
2.940
2.440
2.140
1.840
1.640
1.440
riBP86
0.0
2.6
7.2
18.4
46.8
64.1
57.0
MBPT(2)-fc
The Very End